Questo esercizio è uno delle infinite varianti
del moto centrale. Infatti la superficie su cui è vincolato a muoversi il
punto è invariante per rotazioni intorno all'asse ![]() ,
e lo stesso invarianti
sono i due campi di forza. Ovviamente tale invarianza implicherà
la conservazione del momento della quantità di moto.
,
e lo stesso invarianti
sono i due campi di forza. Ovviamente tale invarianza implicherà
la conservazione del momento della quantità di moto.
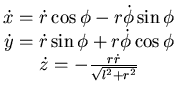 |
(6.49) |
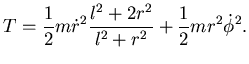
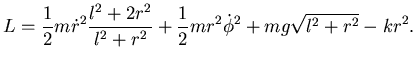
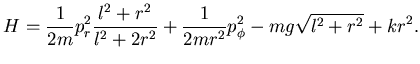
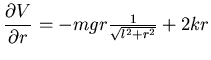 .
Dunque
.
Dunque 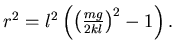 L'equilibrio esiste se e solo se
L'equilibrio esiste se e solo se
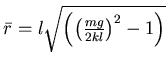 quando esiste reale.
quando esiste reale.
Quante sono le posizioni di equilibrio?
Il potenziale non dipende da ![]() , quindi qualunque sia
, quindi qualunque sia ![]()
![]() e
e
![]() sono posizioni di equilibrio.
D'altra parte se
sono posizioni di equilibrio.
D'altra parte se ![]() , qualunque sia
, qualunque sia ![]() fisicamente
fisicamente
![]() è l'origine del piano.
Dunque se
è l'origine del piano.
Dunque se
![]() c'è solo una posizione di equilibrio,
l'origine del piano; se
c'è solo una posizione di equilibrio,
l'origine del piano; se
![]() esistono
altre infinite posizioni di equilibrio a distanza
esistono
altre infinite posizioni di equilibrio a distanza ![]() dall'origine.
dall'origine.
Sviluppano con Taylor al secondo ordine ![]() intorno a 0
si ottiene
intorno a 0
si ottiene
![]() .
Dunque è stabile se
.
Dunque è stabile se
![]() ed è instabile se
ed è instabile se
![]() .
Considerando anche i termini
.
Considerando anche i termini ![]() si ottiene che il l'origine è stabile anche per
si ottiene che il l'origine è stabile anche per
![]() .
.
Le altre infinite posizioni di equilibrio, quando esistono, sono instabili
pur essendo dei minimi per ![]() considerato nella sola variabile
considerato nella sola variabile ![]() .
Infatti come funzione di
.
Infatti come funzione di ![]() , sono dei minimi non stretti.
La conservazione del momento della quantità di moto
permette di costruire dati inziali arbitrariamente vicini all'equilibrio
che si allontanano.
Per esercizio dai la dimostrazione di questo fatto
usando il metodo utilizzato nel problema 6.1.
, sono dei minimi non stretti.
La conservazione del momento della quantità di moto
permette di costruire dati inziali arbitrariamente vicini all'equilibrio
che si allontanano.
Per esercizio dai la dimostrazione di questo fatto
usando il metodo utilizzato nel problema 6.1.
Per
![]() posso calcolare le
frequenze delle piccole oscillazioni.
Però se procedo come sempre mi accorgo che
la matrice cinetica nel punto di equilibrio
vale
posso calcolare le
frequenze delle piccole oscillazioni.
Però se procedo come sempre mi accorgo che
la matrice cinetica nel punto di equilibrio
vale
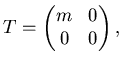 |
(6.50) |
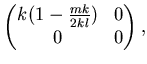 |
(6.51) |
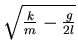 .
Dovè finita l'altra? Perchè il problema è degenere?
Come si procedere correttamente?
.
Dovè finita l'altra? Perchè il problema è degenere?
Come si procedere correttamente?
Il fatto è che l'uso delle coordinate polare è regolare
solo per ![]() . In questo caso siamo in
. In questo caso siamo in ![]() , dunque
per procedere correttamente, bisogna riscrivere la Lagrangiana
in altre coordinate, per esempi
, dunque
per procedere correttamente, bisogna riscrivere la Lagrangiana
in altre coordinate, per esempi ![]() , e studiare le piccole
oscillazioni in
, e studiare le piccole
oscillazioni in ![]() .
Il lettore proceda nel calcolo e verifichi che
tutte e due frequenze di oscillazione sono uguali a
.
Il lettore proceda nel calcolo e verifichi che
tutte e due frequenze di oscillazione sono uguali a
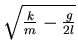 , e che ogni direzione
, e che ogni direzione ![]() è
una direzione normale di oscillazione.
Inoltre provi per esercizio che le orbite delle piccole oscillazioni
sono ellissi con il centro nell'origine.
è
una direzione normale di oscillazione.
Inoltre provi per esercizio che le orbite delle piccole oscillazioni
sono ellissi con il centro nell'origine.
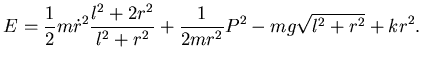
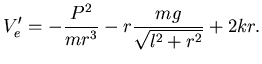
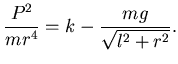
Disegnando il grafico dell'energia potenziale efficace si vede che l'equilibrio è un minimo, quindi è stabile.
Il lettore completi l'esercizio scrivendo le formule di quadratura per il moto complessivo, e discuta qualitativamente il moto.
Si procede nel modo seguente.
Dalla relazione
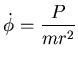 si scopre che la funzione
si scopre che la funzione
![]() è strettamente monotona ( crescente se
è strettamente monotona ( crescente se ![]() è positivo).
Ma allora:
è positivo).
Ma allora:
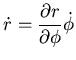 .
Quindi
.
Quindi
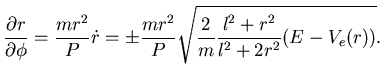
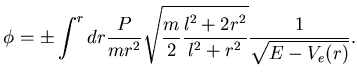
a) Trova almeno due famiglie di moti periodici.
b) Determina le condizioni iniziali tali che il punto
passi per ![]() .
.
c) Studia qualitativamente il moto per i dati iniziali tali che
![]() .
.
d) (**) Scrivere le equazioni del moto nel caso in cui sul punto materiale agisca una forza di attrito proporzionale alla velocità e diretta nel verso opposto della velocità stessa. Provare che l'energia meccanica decresce. Decresce anche il momento della quantità di moto?
Studiare il limite di ![]() per
per
![]() al variare dei dati iniziali.
al variare dei dati iniziali.