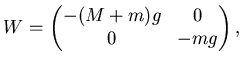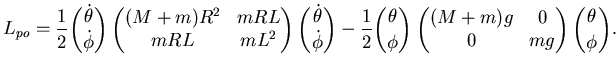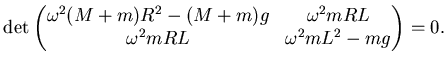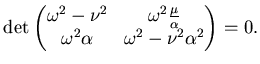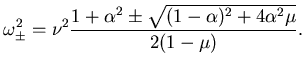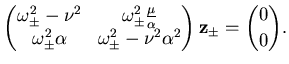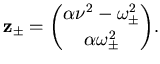


Next: 6.4 Problema
Up: 6 Alcuni esercizi svolti
Previous: 6.2 Problema
Indice
Subsections
6.3 Problema
Un punto materiale di massa 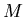 è vincolato a muoversi
senza attrito su una guida circolare verticale di raggio
è vincolato a muoversi
senza attrito su una guida circolare verticale di raggio 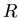 e centro
e centro
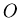 . Un'asta di massa trascurabile, lunga
. Un'asta di massa trascurabile, lunga 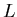 , è fissata al punto materiale
ad un estremo.
, è fissata al punto materiale
ad un estremo.
i) Scrivi le equazioni del moto attraverso la Lagrangiana e l'Hamiltoniana
ii) Determina eventuali integrali primi.
iii) Determina le soluzioni di
equilibrio e discutine la stabilità.
iv) Riduci i gradi di libertà se possibile.
Devi capire di quanti parametri hai bisogno per descrivere
una generica configurazione del sistema.
Per prima cosa bisogna capire
dov'è il punto di massa 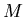 , che chiamerò
, che chiamerò  .
Le sue due coordinate non sono indipendenti, infatti
.
Le sue due coordinate non sono indipendenti, infatti
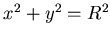 .
La scelta più ragionevole è usare l'angolo al centro che
.
La scelta più ragionevole è usare l'angolo al centro che  forma con l'asse verticale discendente, che chiamerò
forma con l'asse verticale discendente, che chiamerò 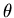 .
Dunque
.
Dunque
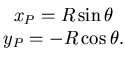 |
(6.24) |
Nota la posizione di  ,
per specificare la posizione del punto di massa
,
per specificare la posizione del punto di massa 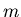 , che chiamerò
, che chiamerò 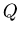 ,
mi serve solo un'altra coordinata, per esempio l'angolo
,
mi serve solo un'altra coordinata, per esempio l'angolo  che l'asta
forma con la verticale discendente per il punto
che l'asta
forma con la verticale discendente per il punto  .
Infatti
.
Infatti
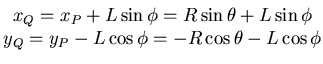 |
(6.25) |
Individuate le coordinate, per il calcolo della Lagrangiana
è necessario calcolare l'energia cinetica e l'energia potenziale
in termini delle coordinate che hai scelto.
L'energia cinetica del sistema è la somma delle energie cinetiche
di tutte le masse in gioco, in questo caso del punto  e del
punto
e del
punto 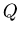 . In coordinate cartesiane:
. In coordinate cartesiane:
Per scrivere 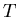 in nelle coordinate lagrangiane, devo
calcolare le velocità. Per il punto
in nelle coordinate lagrangiane, devo
calcolare le velocità. Per il punto  :
:
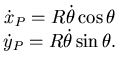 |
(6.26) |
Quindi la sua energia cinetica è
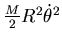 .
.
Per il punto 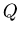 :
:
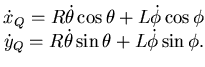 |
(6.27) |
Quindi la sua energia cinetica è :
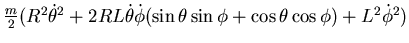 . L'energia cinetica totale è:
. L'energia cinetica totale è:
Per calcolare l'energia potenziale è necessario individuare
tutte le forze attive che agiscono sulle masse.
Su  , l'unica forza attiva è la forza di gravità.
L'energia potenziale di una massa
, l'unica forza attiva è la forza di gravità.
L'energia potenziale di una massa 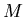 ad una quota
ad una quota 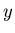 è
è 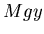 .
Dunque l'energia potenziale per le forze che agiscono su
.
Dunque l'energia potenziale per le forze che agiscono su  è:
è:
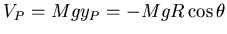 .
L'energia potenziale per le forze che agiscono su
.
L'energia potenziale per le forze che agiscono su 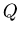 è:
è:
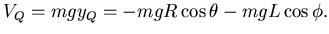
In defintiva l'energia potenziale è :
La Lagrangiana è 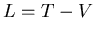 ,
dunque:
,
dunque:
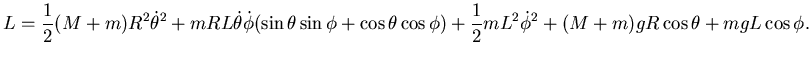 |
(6.28) |
Per scrivere le equazioni del moto, devo prima derivare la
lagrangiana nelle variabili
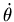 e
e 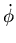 ,
e calcolare quindi gli impulsi coniugati alle variabili
,
e calcolare quindi gli impulsi coniugati alle variabili
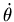 e
e 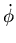 :
:
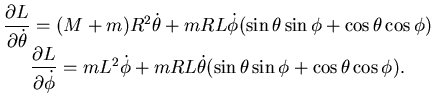 |
(6.29) |
Ora devo considerare gli impulsi coniugati come funzioni del tempo
attraverso le variabili
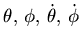 , e
scrivere:
, e
scrivere:
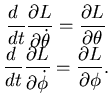 |
(6.30) |
Come prima equazione ottengo
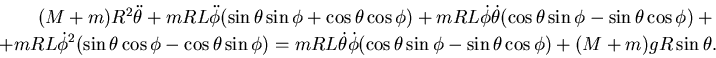 |
(6.31) |
Come seconda equazione ottengo
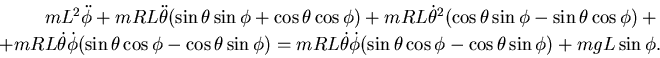 |
(6.32) |
Nota bene.
La derivata rispetto al tempo dei momenti coniugati ha vari termini:
termini lineari nelle derivate seconde rispetto al tempo,
e termini quadratici nelle derivate prime rispetto al tempo.
Per Lagrangiane ``naturali'' non ci posso essere
termini lineari nelle derivate prime (vedi sezione 7,
esercizio 7.1).
Nei membri di destra delle equazioni, non ci sono solo le
derivate dell'energia potenziale con il segno cambiato, ma anche
le derivate rispetto alle variabili della parte cinetica.
Per il calcolo dell'Hamiltoniana si procede come segue.
Per prima cosa si definiscono le nuove variabili, che sono
gli impulsi coniugati:
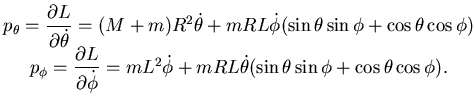 |
(6.33) |
Dopo di che, si ricavano le espressioni di
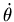 e
e 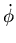 in termini delle nuove variabili.
Per fare questo si deve risolvere il sisitema di equazioni lineare
6.33 rispetto alle variabili
in termini delle nuove variabili.
Per fare questo si deve risolvere il sisitema di equazioni lineare
6.33 rispetto alle variabili
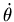 e
e 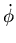 .
Si ottiene:
.
Si ottiene:
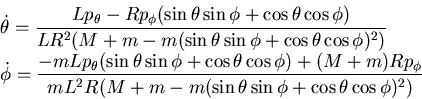 |
(6.34) |
A questo punto l'Hamiltoniana è data da
dove bisogna sostituire a
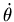 e
e 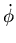 i valori delle espressioni 6.34.
Il lettore completi i calcoli.
i valori delle espressioni 6.34.
Il lettore completi i calcoli.
Una strada leggermente più veloce è la seguente (vedi sezione
7).
Esplicito l'energia cinetica nella Lagrangiana come forma quadratica.
dove 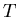 è la matrice cinetica
è la matrice cinetica
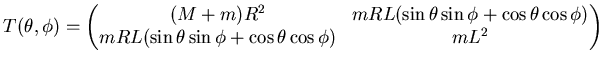 |
(6.35) |
A questo punto l'Hamiltoniana è data da:
dove 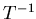 è l'inversa di
è l'inversa di 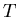 .
Il calcolo dell'inversa della matrice è assolutamente standard.
In realtà l'ho già calcolata prima, quando ho trovato
.
Il calcolo dell'inversa della matrice è assolutamente standard.
In realtà l'ho già calcolata prima, quando ho trovato
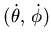 in funzione di
in funzione di
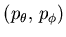 . Infatti
quindi
. Infatti
quindi
In definitiva:
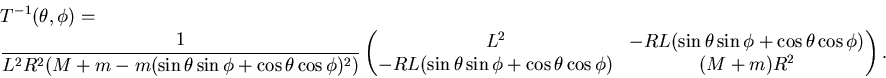 |
(6.36) |
Dunque l'Hamiltoniana è:
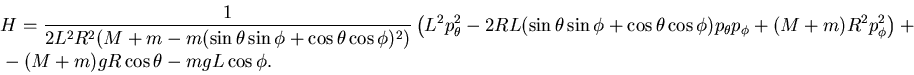 |
(6.37) |
Le equazioni del moto in formalismo hamiltoniano sono
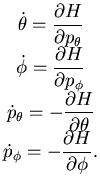 |
(6.38) |
Il lettore completi i calcoli.
Astrattamente, le posizioni di equilibrio in formalismo lagrangiano
si ottengono dalle equazioni trovando i valori di
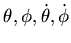 che risolvono identicamente
le equazioni. Ovviamente, essendo il sistema di partenza meccanico,
deve essere
che risolvono identicamente
le equazioni. Ovviamente, essendo il sistema di partenza meccanico,
deve essere
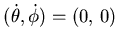 .
Sostituendo questi valori nelle equazioni, le posizioni di equilibrio
si ottengono cercando i valori di
.
Sostituendo questi valori nelle equazioni, le posizioni di equilibrio
si ottengono cercando i valori di 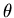 e
e  per cui
per cui
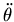 e
e
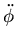 sono nulli.
E' facile rendersi conto che ciò accade se e solo se
sono nulli.
E' facile rendersi conto che ciò accade se e solo se
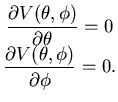 |
(6.39) |
In definitiva le posizioni di equilibrio si ottengono annullando
il gradiente, rispetto alle coordinate lagrangiane, dell'energia
potenziale.
In questo caso:
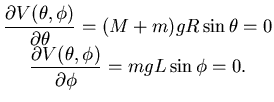 |
(6.40) |
Le soluzioni sono
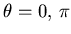 e
e
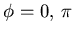 .
Dunque le posizioni di equilibrio sono:
.
Dunque le posizioni di equilibrio sono:
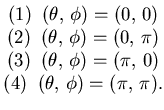 |
(6.41) |
NB: il sistema è fisicamente periodico, nel senso
che la posizione
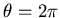 è la stessa di
è la stessa di
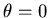 e cosí
via, quindi mi limito a considerare i valori tra 0 e
e cosí
via, quindi mi limito a considerare i valori tra 0 e 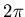 .
.
I punti di minimo dell'energia potenziale sono punti di equilibrio
stabili, i punti non di minimo ( punti di sella e punti di massimo )
sono punti di equilibrio instabili.
Un modo possibile per determinare se un punto critico di 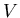 (
cioè un punto in cui
(
cioè un punto in cui 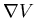 è nullo) è di minimo oppure no,
è quello di calcolare la matrice Hessiana e determinarne il segno
degli autovalori.
è nullo) è di minimo oppure no,
è quello di calcolare la matrice Hessiana e determinarne il segno
degli autovalori.
Procedo al calcolo della matrice Hessiana, che in questo caso
chiamo 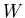 per non confonderla con
per non confonderla con 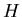 con cui ho indicato
l'Hamiltoniana.
con cui ho indicato
l'Hamiltoniana.
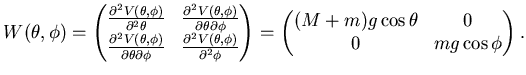 |
(6.42) |
A questo punto la calcolo nelle posizioni di equilibrio e ne
determino gli autovalori.
Caso 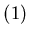 :
:
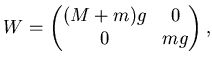 |
(6.43) |
con autovalori 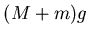 e
e 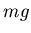 , entrambi positivi, dunque il
punto è di minimo e quindi l'equilibro è stabile.
, entrambi positivi, dunque il
punto è di minimo e quindi l'equilibro è stabile.
Caso 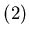 :
:
con autovalori 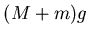 e
e 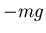 , uno negativo e uno positivo, dunque il
punto è di sella e quindi l'equilibro è instabile.
, uno negativo e uno positivo, dunque il
punto è di sella e quindi l'equilibro è instabile.
Caso 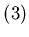 :
:
con autovalori 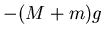 e
e 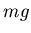 , uno negativo e uno positivo, dunque il
punto è di sella e quindi l'equilibro è instabile.
, uno negativo e uno positivo, dunque il
punto è di sella e quindi l'equilibro è instabile.
Caso 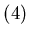 :
:
con autovalori 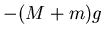 e
e 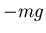 , entrambi negativi, dunque il
punto è di massimo e quindi l'equilibro è instabile.
, entrambi negativi, dunque il
punto è di massimo e quindi l'equilibro è instabile.
Cè una sola posizione di equilibrio stabile, è la 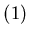 .
Per calcolare il moto delle piccole oscillazioni si può procedere
scrivendo per prima cosa
la Lagrangiana delle piccole oscillazioni intorno alla posizione
di equilibrio.
Bisogna scrivere l'approssimazione al secondo ordine
dell'energia cinetica e dell'energia potenziale.
Per l'energia cinetica è sufficiente calcolare
la matrice cinetica, definita
nell'equazione 6.35,
nella posizione di equilibrio
.
Per calcolare il moto delle piccole oscillazioni si può procedere
scrivendo per prima cosa
la Lagrangiana delle piccole oscillazioni intorno alla posizione
di equilibrio.
Bisogna scrivere l'approssimazione al secondo ordine
dell'energia cinetica e dell'energia potenziale.
Per l'energia cinetica è sufficiente calcolare
la matrice cinetica, definita
nell'equazione 6.35,
nella posizione di equilibrio  .
Per l'energia potenziale è sufficiente calcolare
la matrice Hessiana
.
Per l'energia potenziale è sufficiente calcolare
la matrice Hessiana  nella posizione di equilibrio.
Ho già svolto questo conto nell'equazione
6.43.
In definitiva la Lagrangiana delle piccole oscillazioni
è data da
nella posizione di equilibrio.
Ho già svolto questo conto nell'equazione
6.43.
In definitiva la Lagrangiana delle piccole oscillazioni
è data da
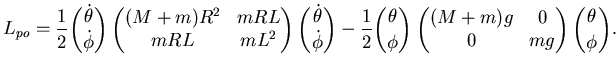 |
(6.44) |
Il problema agli autovettori da risolvere è
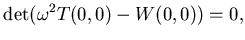 |
(6.45) |
ovvero
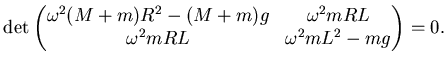 |
(6.46) |
Il calcolo è un pò complicato ma non presenta
nessuna difficoltà concettuale.
Per diminuire la fatica, conviene ricordarsi che
il determinante è una funzione lineare delle singole righe.
In particolare se moltiplico una sola riga per un numero
anche il determinante sarà moltiplicato per lo stesso numero.
Ma allora mi conviene dividere per 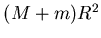 la prima
riga e per
la prima
riga e per 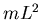 la seconda. Ovviamente i valori di
la seconda. Ovviamente i valori di 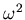 non cambiano.
Introduco anche i parametri
non cambiano.
Introduco anche i parametri
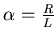 ,
,
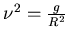 e
e
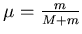 .
L'equazione agli autovalori diventa:
.
L'equazione agli autovalori diventa:
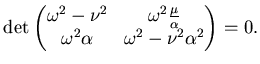 |
(6.47) |
Quindi:
che ha le due soluzioni
Tenedendo presente che 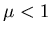 , si riconosce che
, si riconosce che
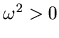 in
entrambi i casi.
Per il calcolo dei corrispondenti autovettori,
dovrei considerare i due sistemi:
in
entrambi i casi.
Per il calcolo dei corrispondenti autovettori,
dovrei considerare i due sistemi:
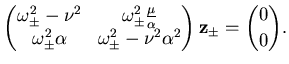 |
(6.48) |
dove le incognite sono i due vettori
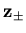 .
Il determinate della matrice è nullo, dunque
per determinare il vettore mi basta considerare,
ad esempio, la seconda riga.
Non normalizzando, posso sceglire:
che sono i modi normali di oscillazione.
.
Il determinate della matrice è nullo, dunque
per determinare il vettore mi basta considerare,
ad esempio, la seconda riga.
Non normalizzando, posso sceglire:
che sono i modi normali di oscillazione.
La Lagrangiana non dipende esplicitamente dal tempo,
dunque l'energia meccanica si conserva.
D'altra parte non ci sono variabili cicliche, né evidenti
simmetrie del problema.
Non avendo a disposizione altri integrali primi non
posso procedere alla riduzione dei gradi di libertà.
Il problema assegnato è formulato in modo dimensionalmente
consistente, infatti 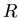 e
e 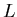 sono due lunghezze,
sono due lunghezze, 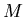 e
e 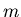 sono
due masse e
sono
due masse e 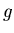 è l'accelerazione di gravità che ha
dimensioni fisiche
è l'accelerazione di gravità che ha
dimensioni fisiche ![$ [L/T^2]$](img1045.png) (lunghezza diviso tempo a quadrato).
Quindi anche i calcoli che avete fatto devono essere
coerenti nelle dimensioni fisiche.
Si può verificare che l'energia cinetica e l'energia potenziale
hanno effettivamente le dimensioni fisiche di un'energia,
etc. .
In particolare le frequenze delle piccole oscillazioni
sono delle frequenze. Infatti
i parametri
(lunghezza diviso tempo a quadrato).
Quindi anche i calcoli che avete fatto devono essere
coerenti nelle dimensioni fisiche.
Si può verificare che l'energia cinetica e l'energia potenziale
hanno effettivamente le dimensioni fisiche di un'energia,
etc. .
In particolare le frequenze delle piccole oscillazioni
sono delle frequenze. Infatti
i parametri 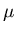 e
e 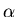 sono adimensionali,
mentre il parametro
sono adimensionali,
mentre il parametro 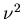 ha le dimensioni di
ha le dimensioni di
![$ [g/R^2]=[1/T^2]$](img1047.png) , cioè di una frequenza al quadrato.
, cioè di una frequenza al quadrato.

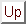


Next: 6.4 Problema
Up: 6 Alcuni esercizi svolti
Previous: 6.2 Problema
Indice
root
2001-04-02
![]() , che chiamerò
, che chiamerò ![]() .
Le sue due coordinate non sono indipendenti, infatti
.
Le sue due coordinate non sono indipendenti, infatti
![]() .
La scelta più ragionevole è usare l'angolo al centro che
.
La scelta più ragionevole è usare l'angolo al centro che ![]() forma con l'asse verticale discendente, che chiamerò
forma con l'asse verticale discendente, che chiamerò ![]() .
Dunque
.
Dunque
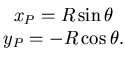
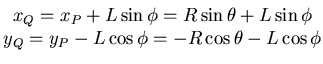
![]() e del
punto
e del
punto ![]() . In coordinate cartesiane:
. In coordinate cartesiane:
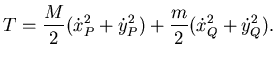
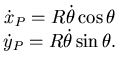
![]() :
:
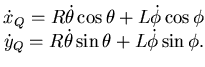
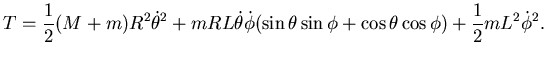
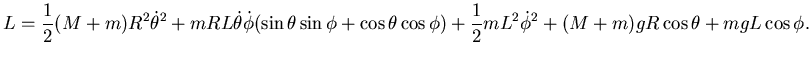
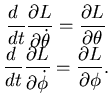
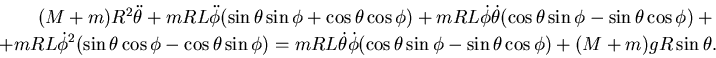
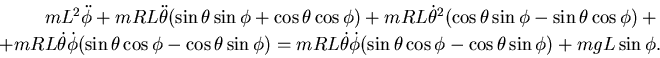
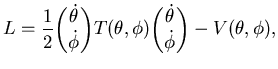
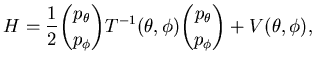
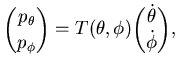
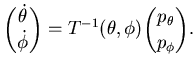
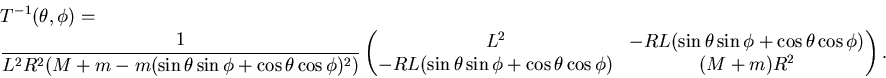
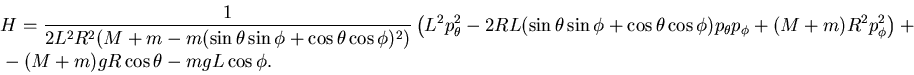
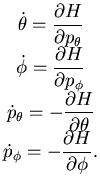
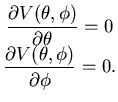
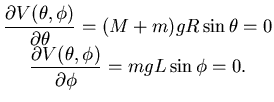
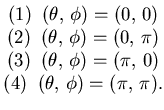
![]() (
cioè un punto in cui
(
cioè un punto in cui ![]() è nullo) è di minimo oppure no,
è quello di calcolare la matrice Hessiana e determinarne il segno
degli autovalori.
è nullo) è di minimo oppure no,
è quello di calcolare la matrice Hessiana e determinarne il segno
degli autovalori.
![]() per non confonderla con
per non confonderla con ![]() con cui ho indicato
l'Hamiltoniana.
con cui ho indicato
l'Hamiltoniana.
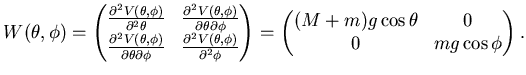
![]() :
:
![]() :
:
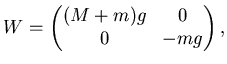
![]() :
:
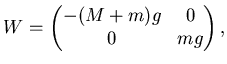
![]() :
: