


Next: 6.2 Problema
Up: 6 Alcuni esercizi svolti
Previous: 6 Alcuni esercizi svolti
Indice
Subsections
6.1 Problema
Un punto materiale di massa 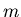 , indicato con
, indicato con  , si muove senza
attrito su una retta orizzontale. Un asta priva di massa e lunga
, si muove senza
attrito su una retta orizzontale. Un asta priva di massa e lunga 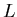 ha un
estremo in
ha un
estremo in  . All'altro estremo è fissato un punto materiale
di massa
. All'altro estremo è fissato un punto materiale
di massa 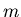 , indicato con Q. Sul sistema agisce la forza di
gravità, nella direzione verticale discendente.
, indicato con Q. Sul sistema agisce la forza di
gravità, nella direzione verticale discendente.
Devi capire di quanti parametri hai bisogno per descrivere
una generica configurazione del sistema.
Per specificare la posizione di  è sufficiente il valore
della sua ascissa, che chiamerò
è sufficiente il valore
della sua ascissa, che chiamerò 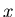 , rispetto ad una origine
fissata arbitrariamente.
In tal caso, detto
, rispetto ad una origine
fissata arbitrariamente.
In tal caso, detto 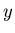 l'asse verticale,
le coordinate di
l'asse verticale,
le coordinate di  saranno
saranno 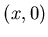 .
Per specificare la posizione di
.
Per specificare la posizione di 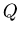 è sufficiente
conoscere, ad esempio, l'angolo che l'asta forma con la verticale
discendente passante per
è sufficiente
conoscere, ad esempio, l'angolo che l'asta forma con la verticale
discendente passante per  , che chiamerò
, che chiamerò  .
Quindi le coordinate di
.
Quindi le coordinate di 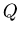 saranno
saranno
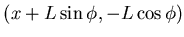 .
Il problema ha dunque due gradi di libertà.
.
Il problema ha dunque due gradi di libertà.
Devo calcolare l'energia cinetica di  e di
e di 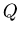 e poi sommarle.
Per far ciò devo calcolare le velocità dei due punti in
termini delle variabili lagrangiane
e poi sommarle.
Per far ciò devo calcolare le velocità dei due punti in
termini delle variabili lagrangiane
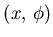 e delle
loro derivate rispetto al tempo.
Evidentemente la velocità del punto
e delle
loro derivate rispetto al tempo.
Evidentemente la velocità del punto  è
è
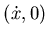 ,
la velocità di
,
la velocità di 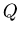 è
è
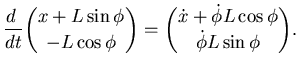 |
(6.1) |
Quadrando e sommando ottengo:
Controllo dimensionale: 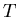 deve avere le dimensioni di una energia,
cioè massa per lunghezza al quadrato su tempo al quadrato.
L'espressione trovata è corretta perché
deve avere le dimensioni di una energia,
cioè massa per lunghezza al quadrato su tempo al quadrato.
L'espressione trovata è corretta perché 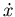 è una velocità,
è una velocità,
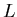 è una lunghezza e
è una lunghezza e 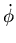 ha le dimensioni dell'inverso del tempo.
ha le dimensioni dell'inverso del tempo.
Devo sommare i contributi dell'energia potenziale, espressi in
variabile lagrangiane, delle forze attive che agiscono sui punti.
In questo caso la forza di gravità non ha effetto su  , che è
vincolato ad una retta orizzontale.
Dunque l'unico contributo all'energia potenziale
è quello gravitazione sul punto
, che è
vincolato ad una retta orizzontale.
Dunque l'unico contributo all'energia potenziale
è quello gravitazione sul punto 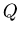 .
L'energia potenziale gravitazionale è data dalla massa per la
quota per l'accelerazione di gravità.
.
L'energia potenziale gravitazionale è data dalla massa per la
quota per l'accelerazione di gravità.
Quindi
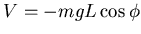 .
.
Per scrivere le equazioni del moto, devo prima derivare la
lagrangiana nelle variabili 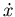 e
e 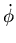 ,
e calcolare quindi gli impulsi coniugati alle variabili
,
e calcolare quindi gli impulsi coniugati alle variabili
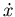 e
e 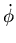 :
:
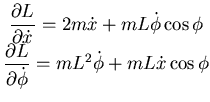 |
(6.2) |
Ora devo considerare gli impulsi coniugati come funzioni del tempo
attraverso le variabili
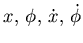 , e
scrivere:
, e
scrivere:
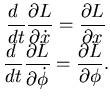 |
(6.3) |
Come prima equazione ottengo
Come seconda
che si può semplificare in:
Verifica che le equzioni sono dimensionalmente corrette, tenendo
presente che 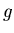 ha le dimensioni di una accelerazione.
ha le dimensioni di una accelerazione.
Per il calcolo dell'Hamiltoniana si procede come segue.
Per prima cosa si definiscono le nuove variabili, che sono
gli impulsi coniugati:
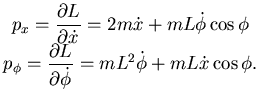 |
(6.4) |
Riconosci che 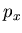 ha le dimensioni di una quantità di moto
(massa per velocità) e che
ha le dimensioni di una quantità di moto
(massa per velocità) e che 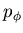 ha le dimensioni di
un momento della quantità di moto (massa per lunghezza per velocità).
ha le dimensioni di
un momento della quantità di moto (massa per lunghezza per velocità).
Dopo di che si ricavano le espressioni di
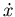 e
e 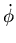 in termini delle nuove variabili.
Per fare questo si deve risolvere il sisitema di equazioni lineare
6.4 rispetto alle variabili
in termini delle nuove variabili.
Per fare questo si deve risolvere il sisitema di equazioni lineare
6.4 rispetto alle variabili
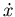 e
e 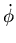 .
Si ottiene:
.
Si ottiene:
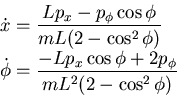 |
(6.5) |
A questo punto l'Hamiltoniana è data da
dove bisogna sostituire a 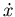 e
e 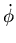 i valori delle espressioni 6.5.
Il lettore completi i calcoli
(per una strada leggermente più veloce vedi sezione
7).
i valori delle espressioni 6.5.
Il lettore completi i calcoli
(per una strada leggermente più veloce vedi sezione
7).
L'espressione dell'Hamiltoniana è:
Il lettore verifichi che tutti i termini hanno le dimensioni di una
energia.
Le equazioni del moto in formalismo hamiltoniano sono
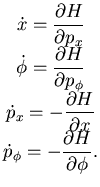 |
(6.6) |
Si ottiene
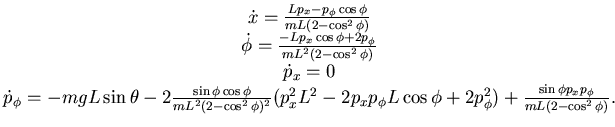 |
(6.7) |
Astrattamente, le posizioni di equilibrio in formalismo lagrangiano
si ottengono dalle equazioni trovando i valori di
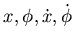 che risolvono identicamente
le equazioni. Ovviamente, essendo il sistema di partenza meccanico,
deve essere
che risolvono identicamente
le equazioni. Ovviamente, essendo il sistema di partenza meccanico,
deve essere
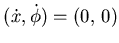 .
Sostituendo questi valori nelle equazioni, le posizioni di equilibrio
si ottengono cercando i valori di
.
Sostituendo questi valori nelle equazioni, le posizioni di equilibrio
si ottengono cercando i valori di 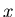 e
e  per cui
per cui
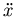 e
e
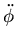 sono nulli.
E' facile rendersi conto che ciò accade se e solo se
sono nulli.
E' facile rendersi conto che ciò accade se e solo se
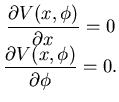 |
(6.8) |
In definitiva le posizioni di equilibrio si ottengono annullando
il gradiente, rispetto alle coordinate lagrangiane, dell'energia
potenziale.
In questo caso 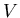 non dipende da
non dipende da 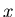 ,
dunque la condizione si riduce a
,
dunque la condizione si riduce a
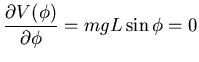 ,
che ha come soluzioni
,
che ha come soluzioni
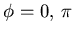 .
(Trascuro i multipli di
.
(Trascuro i multipli di 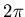 perché fisicamente
le posizioni
perché fisicamente
le posizioni
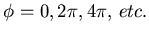 sono indistinguibili).
Quante sono le posizioni di equilbrio?
Ovviamente infinite!
Infatti, qualunque sia
sono indistinguibili).
Quante sono le posizioni di equilbrio?
Ovviamente infinite!
Infatti, qualunque sia 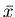 ,
le posizioni
,
le posizioni
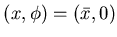 e
e
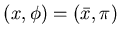 sono di equilibrio: l'asta è verticale e nessuna forza
attiva la sposta se la velocità iniziale è nulla.
sono di equilibrio: l'asta è verticale e nessuna forza
attiva la sposta se la velocità iniziale è nulla.
I punti di minimo stretto dell'energia potenziale sono punti di equilibrio
stabili, i punti non di minimo ( punti di sella e punti di massimo )
sono punti di equilibrio instabili.
È abbastanza evidente che quando
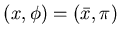 ,
essendo l'asta verticale ma con l'estremo
,
essendo l'asta verticale ma con l'estremo 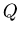 in alto rispetto a
in alto rispetto a  ,
la posizione è instabile.
Infatti l'energia potenziale
,
la posizione è instabile.
Infatti l'energia potenziale
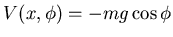 ha
un massimo nella variabile
ha
un massimo nella variabile  quando
quando
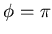 .
.
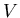 non dipende da
non dipende da 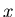 , ma questo implica solo che il massimo di
, ma questo implica solo che il massimo di 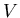 come funzione di due variabili ha un massimo non stretto, nel senso
che è raggiunto qualunque sia
come funzione di due variabili ha un massimo non stretto, nel senso
che è raggiunto qualunque sia 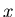 .
.
Le altre posizioni
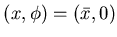 corrispondono
al minimo di
corrispondono
al minimo di 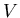 nella variabile
nella variabile  . In questo caso però il
minimo non è stretto, infatti qualunque sia
. In questo caso però il
minimo non è stretto, infatti qualunque sia 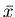 ,
l'energia potenziale assume il valore di minimo.
Questo suggerisce che la posizione sia instabile.
Infatti consideriamo un dato iniziale aribitrariamente vicino,
per esempio
,
l'energia potenziale assume il valore di minimo.
Questo suggerisce che la posizione sia instabile.
Infatti consideriamo un dato iniziale aribitrariamente vicino,
per esempio
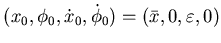 .
La prima equazione di Lagrange mi dice che l'impulso di
conserva (
.
La prima equazione di Lagrange mi dice che l'impulso di
conserva ( 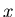 è ciclica).
Dunque, per tutti i tempi:
è ciclica).
Dunque, per tutti i tempi:
Fisicamente, 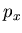 è la quantità di moto totale (verificare!),
ovvero la derivata rispetto al tempo della velocità del baricentro.
Ma allora l'equazione appena scritta
afferma che il baricentro compie un moto rettilineo uniforme.
Quindi se aspetto un tempo sufficiente, il baricentro
sarà arbitrariamente lontano dalla posizione iniziale
che era
è la quantità di moto totale (verificare!),
ovvero la derivata rispetto al tempo della velocità del baricentro.
Ma allora l'equazione appena scritta
afferma che il baricentro compie un moto rettilineo uniforme.
Quindi se aspetto un tempo sufficiente, il baricentro
sarà arbitrariamente lontano dalla posizione iniziale
che era 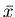 .
Più formalmente,
integrando nel tempo l'equazione appena scritta, e ricordandomi
che
.
Più formalmente,
integrando nel tempo l'equazione appena scritta, e ricordandomi
che
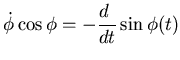 ,
ottengo
Ma allora
,
ottengo
Ma allora
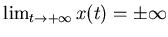 (a seconda del segno di
(a seconda del segno di
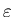 ), infatti qualunque sia la legge
oraria per
), infatti qualunque sia la legge
oraria per 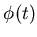 , la funzione
, la funzione
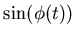 è limitata.
è limitata.
Non ci sono posizioni di equilibrio stabili,
quindi non ha senso parlare di piccole oscillazioni del
moto nelle due variabili. Si potranno considerare
le piccole oscillazioni del moto unidimensionale al
quale posso ridurre il moto per la conservazione della
quantità di moto.
La Lagrangiana non dipende dal tempo,
dunque l'energia meccanica 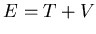 si conserva.
si conserva.
Inoltre, come già visto, l'equazione di Lagrange relativa ad
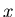 , afferma che
, afferma che
Infatti la variabile 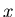 è ciclica, cioè
è ciclica, cioè 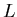 non
dipende da
non
dipende da 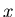 .
Quindi
.
Quindi 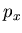 , che nel seguito indico con
, che nel seguito indico con  ,
si conserva.
,
si conserva.
Avendo a disposizione due integrali primi
per un problema a due gradi di libertà, posso ridurre ad uno i gradi
di libertà e portare il moto alle quadrature
(cioè scrivere, almeno in forma implicita, la soluzione
delle equazioni del moto).
Si procede cosí:
scrivo l'energia meccanica, che è una quantità conservata:
Usando la relazione
ricavo
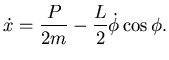 |
(6.9) |
Sostituisco il valore trovato nell'espressione per 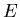 :
Poiché
:
Poiché 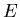 si conserva anche dopo aver sostituito a
si conserva anche dopo aver sostituito a 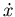 la sua espressione in termini di
la sua espressione in termini di 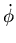 e dell'altro integrale
primo del moto,
dall'espressione di
e dell'altro integrale
primo del moto,
dall'espressione di 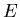 posso ottenere la formula di quadratura
attraverso il solito procedimento: ricavo
posso ottenere la formula di quadratura
attraverso il solito procedimento: ricavo 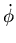 in termini di
in termini di
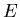 e
e  e integro.
e integro.
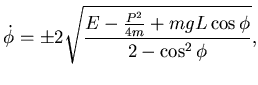 |
(6.10) |
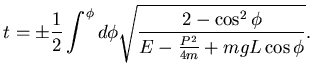 |
(6.11) |
Questa espressioni differiscono da quelle tipiche
dei moti unidimensionale solo per la presenza
del fattore
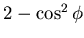 , che comunque è sempre
postivo. Dunque per l'analisi qualitativa del moto limitata
alla variabile
, che comunque è sempre
postivo. Dunque per l'analisi qualitativa del moto limitata
alla variabile  si procede come sempre.
si procede come sempre.
In particolare,
se l'energia meccanica e l'impulso  sono tali che
sono tali che
a)
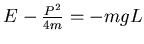 :
: 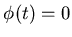 (equilibrio STABILE
per il moto nella sola variabile
(equilibrio STABILE
per il moto nella sola variabile  )
)
b)
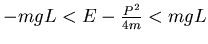 : il moto in
: il moto in  è periodico.
è periodico.
c)
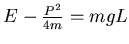 : o
: o
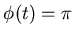 (equilibrio INSTABILE),
oppure
(equilibrio INSTABILE),
oppure  compie un moto a meta asintotica.
compie un moto a meta asintotica.
d)
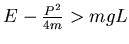 :
:  compie periodicamente tutta
la rotazione tra 0 e
compie periodicamente tutta
la rotazione tra 0 e 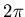 .
.
Domande: Perché non è possibile che
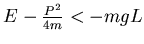 ?
Scrivi il periodo nei casi b) e d). (*) Calcola il periodo delle piccole
oscillazioni intorno alla posizione di equilibrio stabile
?
Scrivi il periodo nei casi b) e d). (*) Calcola il periodo delle piccole
oscillazioni intorno alla posizione di equilibrio stabile 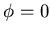 e
confrontalo con in periodo delle piccole oscillazioni che avresti
nel caso che l'altro estremo dell'asta fosse fisso (risposta:
è
e
confrontalo con in periodo delle piccole oscillazioni che avresti
nel caso che l'altro estremo dell'asta fosse fisso (risposta:
è 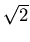 volte più grande).
volte più grande).
Osservazione: Ai fini dell'analisi qualitativa, limitata
alla variabile  , potevo sostituire
, potevo sostituire
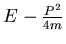 con
con 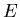 ,
infatti
,
infatti
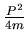 è costante. L'ho lasciato com era per
non perdere traccia dell'energia meccanica del sistema nelle
due variabili.
è costante. L'ho lasciato com era per
non perdere traccia dell'energia meccanica del sistema nelle
due variabili.
Una volta noto, attreverso la formula di quadratura
6.11, il moto nella variabile  ,
l'equazione 6.9 mi dice come è il moto nella variabile
,
l'equazione 6.9 mi dice come è il moto nella variabile 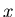 .
Infatti, integrando rispetto al tempo:
.
Infatti, integrando rispetto al tempo:
A questo punto si può rispondere anche ad altre eventuali domande:
a) Per quali valori iniziali il moto è limitato?
b) Trova almeno un moto periodico.
c) È possibile che l'asta rimanga verticale per tutti i tempi? In
tal caso il sistema si può muovere? E che moto fà?
Risposte:
a) Se e solo se 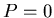 .
.
b) Il moto è periodico se 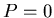 e
e
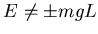 .
.
c) Si, si, rettilineo uniforme.
Nelle equazioni di Hamilton che ho già scritto,
c'è già la riduzione del grado di libertà.
Infatti le equazioni per 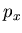 e
e 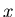 mi dicono che
mi dicono che
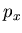 si conserva (
si conserva (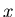 è ciclica)
e che la derivata rispetto al tempo di
è ciclica)
e che la derivata rispetto al tempo di 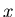 dipende solo
dalla costante
dipende solo
dalla costante 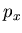 e dal moto nella variabile
e dal moto nella variabile  .
Le equazioni per
.
Le equazioni per  dipendono solo dalla costante
dipendono solo dalla costante 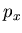 .
Ma allora posso pensare direttamente ad
.
Ma allora posso pensare direttamente ad
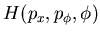 come ad una Hamiltoniana ad un grado di libertà (
come ad una Hamiltoniana ad un grado di libertà ( ),
con
),
con 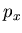 parametro.
parametro.
Potrei a questo punto fare la trasformazione inversa
nelle sole variabili 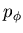 ,
, 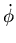 per riottenere
la lagrangiana unidimensionale. In realtà
si può procedere all'analisi qualitativa del moto in
per riottenere
la lagrangiana unidimensionale. In realtà
si può procedere all'analisi qualitativa del moto in
 e ottenere la formula di quadratura, direttamente
nel formalismo Hamiltoniano.
Infatti la stessa
e ottenere la formula di quadratura, direttamente
nel formalismo Hamiltoniano.
Infatti la stessa 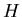 è un integrale primo del moto (si conserva
perché non dipende dal tempo, e infatti coincide con l'energia
meccanica scritta in variabili hamiltoniane).
Ma allora dall'espressione di
è un integrale primo del moto (si conserva
perché non dipende dal tempo, e infatti coincide con l'energia
meccanica scritta in variabili hamiltoniane).
Ma allora dall'espressione di 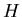 posso ricavare
posso ricavare 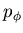 in
termini di
in
termini di  , e sostituendo tale espressione nell'
equazione per
, e sostituendo tale espressione nell'
equazione per  ottenere finalmente
ottenere finalmente  in funzione degli integrali primi e della sola coordinata
in funzione degli integrali primi e della sola coordinata  .
Per esercizio verifica che ottieni gli stessi risultati della
sezione precedente.
.
Per esercizio verifica che ottieni gli stessi risultati della
sezione precedente.



Next: 6.2 Problema
Up: 6 Alcuni esercizi svolti
Previous: 6 Alcuni esercizi svolti
Indice
root
2001-04-02
![]() è sufficiente il valore
della sua ascissa, che chiamerò
è sufficiente il valore
della sua ascissa, che chiamerò ![]() , rispetto ad una origine
fissata arbitrariamente.
In tal caso, detto
, rispetto ad una origine
fissata arbitrariamente.
In tal caso, detto ![]() l'asse verticale,
le coordinate di
l'asse verticale,
le coordinate di ![]() saranno
saranno ![]() .
Per specificare la posizione di
.
Per specificare la posizione di ![]() è sufficiente
conoscere, ad esempio, l'angolo che l'asta forma con la verticale
discendente passante per
è sufficiente
conoscere, ad esempio, l'angolo che l'asta forma con la verticale
discendente passante per ![]() , che chiamerò
, che chiamerò ![]() .
Quindi le coordinate di
.
Quindi le coordinate di ![]() saranno
saranno
![]() .
Il problema ha dunque due gradi di libertà.
.
Il problema ha dunque due gradi di libertà.
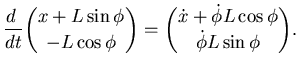
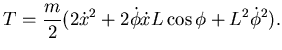
![]() , che è
vincolato ad una retta orizzontale.
Dunque l'unico contributo all'energia potenziale
è quello gravitazione sul punto
, che è
vincolato ad una retta orizzontale.
Dunque l'unico contributo all'energia potenziale
è quello gravitazione sul punto ![]() .
L'energia potenziale gravitazionale è data dalla massa per la
quota per l'accelerazione di gravità.
.
L'energia potenziale gravitazionale è data dalla massa per la
quota per l'accelerazione di gravità.
![]() .
.
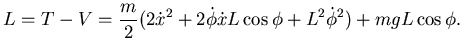
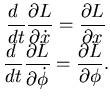
![]() e
e ![]() in termini delle nuove variabili.
Per fare questo si deve risolvere il sisitema di equazioni lineare
6.4 rispetto alle variabili
in termini delle nuove variabili.
Per fare questo si deve risolvere il sisitema di equazioni lineare
6.4 rispetto alle variabili
![]() e
e ![]() .
Si ottiene:
.
Si ottiene:
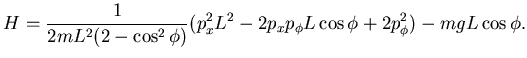
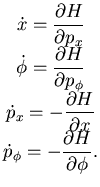
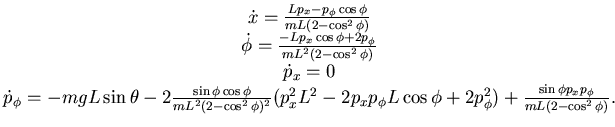
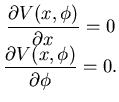
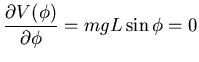 ,
che ha come soluzioni
,
che ha come soluzioni
![]() ,
essendo l'asta verticale ma con l'estremo
,
essendo l'asta verticale ma con l'estremo ![]() in alto rispetto a
in alto rispetto a ![]() ,
la posizione è instabile.
Infatti l'energia potenziale
,
la posizione è instabile.
Infatti l'energia potenziale
![]() ha
un massimo nella variabile
ha
un massimo nella variabile ![]() quando
quando
![]() .
.
![]() non dipende da
non dipende da ![]() , ma questo implica solo che il massimo di
, ma questo implica solo che il massimo di ![]() come funzione di due variabili ha un massimo non stretto, nel senso
che è raggiunto qualunque sia
come funzione di due variabili ha un massimo non stretto, nel senso
che è raggiunto qualunque sia ![]() .
.
![]() corrispondono
al minimo di
corrispondono
al minimo di ![]() nella variabile
nella variabile ![]() . In questo caso però il
minimo non è stretto, infatti qualunque sia
. In questo caso però il
minimo non è stretto, infatti qualunque sia ![]() ,
l'energia potenziale assume il valore di minimo.
Questo suggerisce che la posizione sia instabile.
Infatti consideriamo un dato iniziale aribitrariamente vicino,
per esempio
,
l'energia potenziale assume il valore di minimo.
Questo suggerisce che la posizione sia instabile.
Infatti consideriamo un dato iniziale aribitrariamente vicino,
per esempio
![]() .
La prima equazione di Lagrange mi dice che l'impulso di
conserva (
.
La prima equazione di Lagrange mi dice che l'impulso di
conserva ( ![]() è ciclica).
Dunque, per tutti i tempi:
è ciclica).
Dunque, per tutti i tempi:
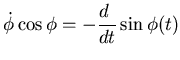 ,
ottengo
,
ottengo
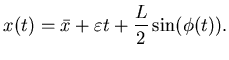
![]() , afferma che
, afferma che
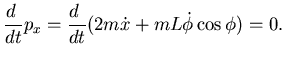
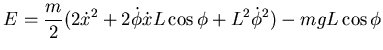
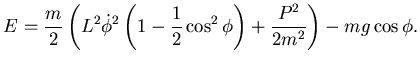
![]() sono tali che
sono tali che
![]() :
: ![]() (equilibrio STABILE
per il moto nella sola variabile
(equilibrio STABILE
per il moto nella sola variabile ![]() )
)
![]() : il moto in
: il moto in ![]() è periodico.
è periodico.
![]() : o
: o
![]() (equilibrio INSTABILE),
oppure
(equilibrio INSTABILE),
oppure ![]() compie un moto a meta asintotica.
compie un moto a meta asintotica.
![]() :
: ![]() compie periodicamente tutta
la rotazione tra 0 e
compie periodicamente tutta
la rotazione tra 0 e ![]() .
.
![]() ?
Scrivi il periodo nei casi b) e d). (*) Calcola il periodo delle piccole
oscillazioni intorno alla posizione di equilibrio stabile
?
Scrivi il periodo nei casi b) e d). (*) Calcola il periodo delle piccole
oscillazioni intorno alla posizione di equilibrio stabile ![]() e
confrontalo con in periodo delle piccole oscillazioni che avresti
nel caso che l'altro estremo dell'asta fosse fisso (risposta:
è
e
confrontalo con in periodo delle piccole oscillazioni che avresti
nel caso che l'altro estremo dell'asta fosse fisso (risposta:
è ![]() volte più grande).
volte più grande).
![]() , potevo sostituire
, potevo sostituire
![]() con
con ![]() ,
infatti
,
infatti
![]() è costante. L'ho lasciato com era per
non perdere traccia dell'energia meccanica del sistema nelle
due variabili.
è costante. L'ho lasciato com era per
non perdere traccia dell'energia meccanica del sistema nelle
due variabili.
![]() ,
l'equazione 6.9 mi dice come è il moto nella variabile
,
l'equazione 6.9 mi dice come è il moto nella variabile ![]() .
Infatti, integrando rispetto al tempo:
.
Infatti, integrando rispetto al tempo:
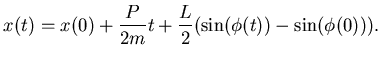
![]() .
.
![]() e
e
![]() .
.
![]() ,
, ![]() per riottenere
la lagrangiana unidimensionale. In realtà
si può procedere all'analisi qualitativa del moto in
per riottenere
la lagrangiana unidimensionale. In realtà
si può procedere all'analisi qualitativa del moto in
![]() e ottenere la formula di quadratura, direttamente
nel formalismo Hamiltoniano.
Infatti la stessa
e ottenere la formula di quadratura, direttamente
nel formalismo Hamiltoniano.
Infatti la stessa ![]() è un integrale primo del moto (si conserva
perché non dipende dal tempo, e infatti coincide con l'energia
meccanica scritta in variabili hamiltoniane).
Ma allora dall'espressione di
è un integrale primo del moto (si conserva
perché non dipende dal tempo, e infatti coincide con l'energia
meccanica scritta in variabili hamiltoniane).
Ma allora dall'espressione di ![]() posso ricavare
posso ricavare ![]() in
termini di
in
termini di ![]() , e sostituendo tale espressione nell'
equazione per
, e sostituendo tale espressione nell'
equazione per ![]() ottenere finalmente
ottenere finalmente ![]() in funzione degli integrali primi e della sola coordinata
in funzione degli integrali primi e della sola coordinata ![]() .
Per esercizio verifica che ottieni gli stessi risultati della
sezione precedente.
.
Per esercizio verifica che ottieni gli stessi risultati della
sezione precedente.