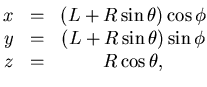6.5 Problema

Un punto materiale di massa $m$ è vincolato a muoversi sulla superficie di un toro, di equazione parametrica

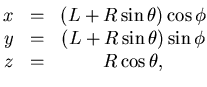$$\begin{matrix}x& = & (L+R\sin \theta) \cos \phi y& = & (L+R\sin \theta) \sin \phi z& = & R\cos \theta, \end{matrix}$$ (6.52)

con $R<L$. La superficie assegnata è un toro in $\mathbb{R}^3$.

Caso 1 La forza di gravità agisce lungo l'asse delle $z$ nella direzione discendente.

Caso 2 La forza di gravità agisce lungo l'asse delle $x$ nella direzione decrescente.

Caso 3 La forza di gravità è trascurabile.

Per tutti e tre i casi:

a) Scrivi le equazioni del moto.

b) Determina eventuali integrali primi.

c) Determina le soluzioni di equilibrio e discutine la stabilità.

d) Riduci i gradi di libertà se possibile e analizza qualitativamenteil moto.

e) Nei casi 1) e 3) si considerino i moti di momento della quantità di moto non nullo. Si provi che tra essi, in entrambi i casi, esistono due moti periodici distinti. Si trovi inoltre almeno un'altra famiglia di dati iniziali per cui il moto è periodico.

f) Nel caso 1) si consideri il moto periodico di momento assegnato e si calcoli la reazione del vincolo durante il moto.