Next: 6.3 Problema
Up: 6 Alcuni esercizi svolti
Previous: 6.1 Problema
Indice
Subsections
6.2 Problema
Un punto materiale di massa 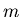 , indicato con
, indicato con 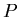 , si muove senza
attrito su una retta orizzontale. Un asta priva di massa e lunga
, si muove senza
attrito su una retta orizzontale. Un asta priva di massa e lunga 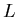 ha un
estremo in
ha un
estremo in 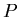 . All'altro estremo è fissato un punto materiale
di massa
. All'altro estremo è fissato un punto materiale
di massa 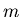 , indicato con Q. Sul sistema agisce la forza di
gravità, nella direzione verticale discendente; inoltre una molla
di costante elastica
, indicato con Q. Sul sistema agisce la forza di
gravità, nella direzione verticale discendente; inoltre una molla
di costante elastica 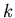 lega il punto materiale
lega il punto materiale 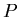 ad un punto fisso
ad un punto fisso 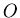 della retta.
della retta.
Evidentemente questo problema differisce dal precedente solo per
la presenza della molla.
Dunque per la Lagrangiana e l'Hamiltoniana devo solo
aggiungere il contributo dell'energia potenziale della
molla, che è
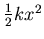 .
.
Quindi:
La presenza di questo ulteriore termine ha come conseguenza
che il problema non è più invariante per traslazioni ( e infatti
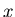 in questo caso non è ciclica).
in questo caso non è ciclica).
Il gradiente dell'energia è
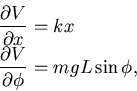 |
(6.12) |
che è nullo se e solo se
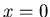 e
e
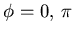 .
Le posizioni di equilibrio sono dunque
.
Le posizioni di equilibrio sono dunque
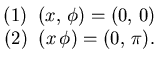 |
(6.13) |
Dal fatto che 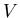 sia la somma di due funzioni una dipendente
solo da
sia la somma di due funzioni una dipendente
solo da 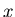 e l'altra dipendente solo da
e l'altra dipendente solo da 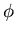 , risulta
evidente che (1) è il minimo assoluto dell'energia potenziale
e (2) è un punto di sella.
Dunque (1) è stabile e (2) è instabile.
In ogni caso, procedo al calcolo della matrice Hessiana, che in questo caso
chiamo
, risulta
evidente che (1) è il minimo assoluto dell'energia potenziale
e (2) è un punto di sella.
Dunque (1) è stabile e (2) è instabile.
In ogni caso, procedo al calcolo della matrice Hessiana, che in questo caso
chiamo 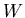 :
:
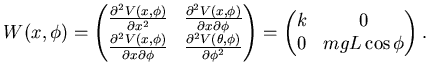 |
(6.14) |
A questo punto la calcolo nelle posizioni di equilibrio e ne
determino gli autovalori.
Nel caso (1)
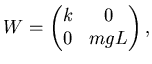 |
(6.15) |
con autovalori 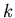 e
e 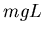 , entrambi positivi, dunque il
punto è di minimo e quindi l'equilibro è stabile.
Nel caso (2)
, entrambi positivi, dunque il
punto è di minimo e quindi l'equilibro è stabile.
Nel caso (2)
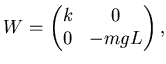 |
(6.16) |
con autovalori 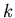 e
e 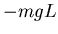 , uno positivo e uno negativo, dunque il
punto è di sella e quindi l'equilibro è instabile.
, uno positivo e uno negativo, dunque il
punto è di sella e quindi l'equilibro è instabile.
(1) è la sola posizione di equilibrio stabile.
Per procedere nel calcolo della frequenza delle piccole
oscillazioni e dei modi normali
devo considerare l'approssimazione quadratica dell'energia cinetica
e dell'energia potenziale
(vedi sezione 7).
Per l'energia cinetica è sufficiente calcolare
la matrice cinetica,
nella posizione di equilibrio 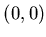 .
Chi è la matrice cinetica?
È la matrice attraverso la quale esprimi
l'energia cinetica. Puoi riscrivere l'energia cinetica come
.
Chi è la matrice cinetica?
È la matrice attraverso la quale esprimi
l'energia cinetica. Puoi riscrivere l'energia cinetica come
La matrice cinetica che chiamo 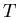 ( da non confondere con
il
( da non confondere con
il 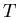 con cui precedentemente ho espresso il valore dell'energia
cinetica), calcolata nella posizione di equilibrio è
Per l'energia potenziale è sufficiente calcolare
la matrice Hessiana
con cui precedentemente ho espresso il valore dell'energia
cinetica), calcolata nella posizione di equilibrio è
Per l'energia potenziale è sufficiente calcolare
la matrice Hessiana 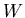 nella posizione di equilibrio.
Ho già svolto questo conto.
nella posizione di equilibrio.
Ho già svolto questo conto.
Il problema agli autovalori risolto dalle
frequenze delle piccole oscillazioni è
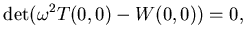 |
(6.17) |
ovvero
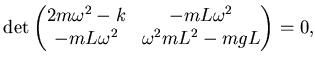 |
(6.18) |
che è l'equazione:
che ha soluzioni:
Entrambi i valori sono positivi, come deve essere.
Quindi ho trovato le frequenze.
Verifica che 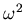 ha le dimensioni fisiche del quadrato
di una frequenza, cioè del quadrato dell'inverso del tempo.
Per il calcolo dei corrispondenti autovettori,
devo considerare i due sistemi:
ha le dimensioni fisiche del quadrato
di una frequenza, cioè del quadrato dell'inverso del tempo.
Per il calcolo dei corrispondenti autovettori,
devo considerare i due sistemi:
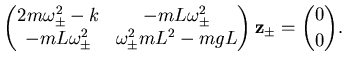 |
(6.19) |
uno per ogni scelta di 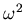 .
Il determinante della matrice è 0,
quindi i vettori
.
Il determinante della matrice è 0,
quindi i vettori 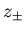 che verificano il sistema
sono della forma:
Osservo che per la scelta
che verificano il sistema
sono della forma:
Osservo che per la scelta 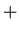 entrambi i valori sono positivi,
quindi l'oscillazione di questo modo normale, che è quello a frequenza
più alta, prevede che
entrambi i valori sono positivi,
quindi l'oscillazione di questo modo normale, che è quello a frequenza
più alta, prevede che 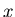 e
e 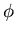 abbiano lo stesso segno.
Pee la scelta
abbiano lo stesso segno.
Pee la scelta 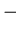 , il termine
, il termine
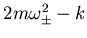 è negativo.
Dunque per questo modo normale di oscillazione, quando
è negativo.
Dunque per questo modo normale di oscillazione, quando 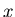 è
positivo
è
positivo 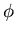 è negativo e viceversa.
è negativo e viceversa.
Calcolare la reazione dei vincoli si 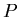 e su
e su 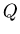 nella configurazione
nella configurazione 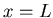 ,
,
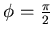 ,
,
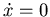 e
e
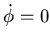 .
.
La teoria generale dei moti vincolati afferma che lungo il moto
la massa per l'accelerazione ( in coordinate cartesiane ) di un punto
uguaglia le forze attive più le reazioni vincolari.
Nel nostro caso:
dove
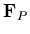 è la risultante delle forze attive
su
è la risultante delle forze attive
su 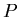 ,
,
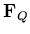 è la risultante delle forze attive
su
è la risultante delle forze attive
su 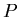 , e
, e 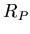 e
e 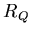 sono le reazioni che i vincoli
esercitano rispettivamente su
sono le reazioni che i vincoli
esercitano rispettivamente su 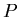 e su
e su 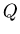 .
Per trovare le espressioni di
.
Per trovare le espressioni di 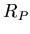 e
e 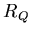 ho bisogno
delle espressioni delle risultanti delle forze attive
e delle accelerazioni in termini
delle coordinate lagrangiane.
ho bisogno
delle espressioni delle risultanti delle forze attive
e delle accelerazioni in termini
delle coordinate lagrangiane.
Procedo con il calcolo delle forze attive.
Sul punto 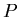 agiscono due forze:
la forza di gravità che è
agiscono due forze:
la forza di gravità che è
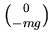 e la
forza di richiamo della molla, che è
e la
forza di richiamo della molla, che è
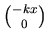 .
Dunque
.
Dunque
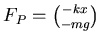 .
Analogamente per
.
Analogamente per 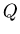 :
:
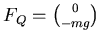 .
Per il calcolo delle accelerazioni devo solo derivare
rispetto al tempo le espressioni per le velocità che
ho già trovato quando ho calcolato l'energia cinetica.
Allora:
.
Per il calcolo delle accelerazioni devo solo derivare
rispetto al tempo le espressioni per le velocità che
ho già trovato quando ho calcolato l'energia cinetica.
Allora:
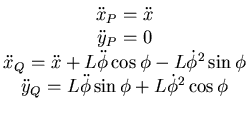 |
(6.20) |
A questo punto sostituisco a 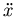 e
e
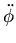 le
loro espressioni in termini di
le
loro espressioni in termini di
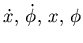 ,
che ottengo dalle equazioni del moto, che sono
,
che ottengo dalle equazioni del moto, che sono
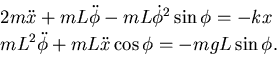 |
(6.21) |
Risolvendo questo sistema in 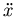 e
e
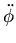 ottieni:
ottieni:
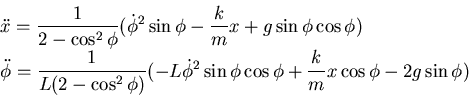 |
(6.22) |
A questo punto puoi ottenere le espressioni per le reazioni vincolari.
Faccio notare che le reazioni vincolari sono forze che dipendono dalla
velocità.
Nel caso paricolare assegnato, essendo
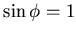 ,
,
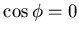 e
e
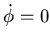 , le espressioni precedenti sono particolarmente
semplici:
, le espressioni precedenti sono particolarmente
semplici:
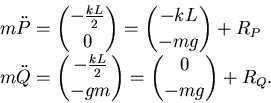 |
(6.23) |
Dunque la reazione vincolare su 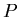 è
è 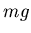 sull'asse verticale
e
sull'asse verticale
e
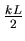 su quello orizzontale;
la reazione su
su quello orizzontale;
la reazione su 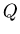 è
è
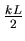 sull'asse orizzontale e nulla
sull'asse verticale.
Dai l'interpretazione fisica di questo fatto.
sull'asse orizzontale e nulla
sull'asse verticale.
Dai l'interpretazione fisica di questo fatto.




Next: 6.3 Problema
Up: 6 Alcuni esercizi svolti
Previous: 6.1 Problema
Indice
root
2001-04-02
![]() .
.
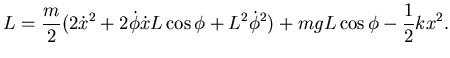
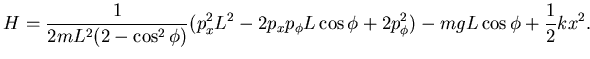
![]() in questo caso non è ciclica).
in questo caso non è ciclica).
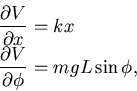
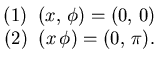
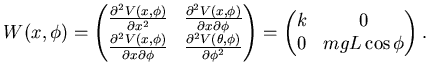
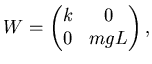
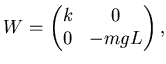
![]() .
Chi è la matrice cinetica?
È la matrice attraverso la quale esprimi
l'energia cinetica. Puoi riscrivere l'energia cinetica come
.
Chi è la matrice cinetica?
È la matrice attraverso la quale esprimi
l'energia cinetica. Puoi riscrivere l'energia cinetica come
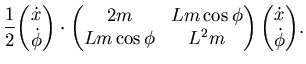
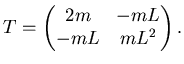
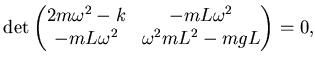
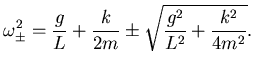
![]() ha le dimensioni fisiche del quadrato
di una frequenza, cioè del quadrato dell'inverso del tempo.
Per il calcolo dei corrispondenti autovettori,
devo considerare i due sistemi:
ha le dimensioni fisiche del quadrato
di una frequenza, cioè del quadrato dell'inverso del tempo.
Per il calcolo dei corrispondenti autovettori,
devo considerare i due sistemi:
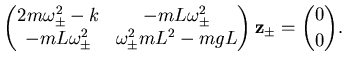
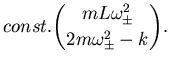
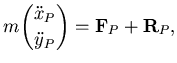
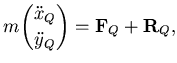
![]() agiscono due forze:
la forza di gravità che è
agiscono due forze:
la forza di gravità che è
![]() e la
forza di richiamo della molla, che è
e la
forza di richiamo della molla, che è
![]() .
Dunque
.
Dunque
![]() .
Analogamente per
.
Analogamente per ![]() :
:
![]() .
Per il calcolo delle accelerazioni devo solo derivare
rispetto al tempo le espressioni per le velocità che
ho già trovato quando ho calcolato l'energia cinetica.
Allora:
.
Per il calcolo delle accelerazioni devo solo derivare
rispetto al tempo le espressioni per le velocità che
ho già trovato quando ho calcolato l'energia cinetica.
Allora:
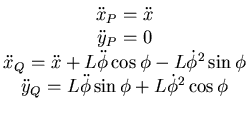
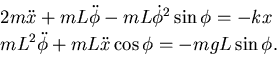
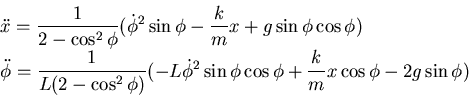
![]() ,
,
![]() e
e
![]() , le espressioni precedenti sono particolarmente
semplici:
, le espressioni precedenti sono particolarmente
semplici: