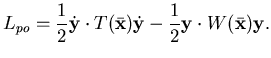Next: 8 Bignamino di Formalismo
Up: Esercitazioni di Meccanica Razionale
Previous: 6.5 Problema
Indice
7 Le Lagrangiane e le Hamiltoniane ``tipiche''
Una Lagrangiana che si ottiene da un sistema fisico
conservativo in un sistema
di riferimento inerziale, con forze puramente posizionali e vincoli
perfetti bilateri è sempre del tipo
dove
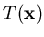 è una matrice simmetrica e definita positiva, e
è una matrice simmetrica e definita positiva, e
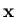 ,
,
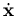 sono in
sono in
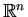 .
Le equazioni del moto si possono sinteticamente scrivere come
.
Le equazioni del moto si possono sinteticamente scrivere come
Esercizio 7.1
Sia
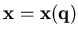
una funzione regolare
da
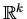
in
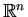
, con
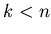
.
Sto pensando che
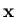
sono le coordinate cartesiane e che
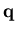
siano le coordiante lagrangiane necessarie per
descrivere i vincoli che deve soddisfare
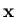
.
Assumo inoltre che le
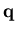
siano delle buone coordinate,
cioè la matrice
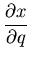
abbia sempre rango massimo
(in questo caso
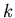
).
Prova che
a)
(ovviamente è un prodotto righe per colonne).
b)
dove la matrice cinetica è data da
(
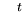
indica la matrice trasposta).
c)
La matrice 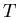 è simmetrica e definita positiva.
è simmetrica e definita positiva.
Il pasaggio all'Hamiltoniana è semplice. Infatti
il vettore degli impulsi coniugati è dato da:
ed essendo 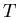 definita positiva, in particolare è invertibile.
Dunque
Ma allora l'Hamiltoniana è data da:
Quindi per il calcolo dell'Hamiltoniana è sufficiente
calcolare l'inversa della matrice
definita positiva, in particolare è invertibile.
Dunque
Ma allora l'Hamiltoniana è data da:
Quindi per il calcolo dell'Hamiltoniana è sufficiente
calcolare l'inversa della matrice 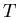 .
.
Esercizio 7.3
Verifica che data una Hamiltoniana
dove
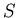
è una matrice simmetrica
e definita positiva, la corrispondente lagrangiana è data da
Esercizio 7.4
Verifica che data una Hamiltoniana
dove
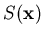
è una matrice simmetrica
e definita positiva, e
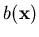
è un vettore,
la corrispondente lagrangiana è data da
Le equazioni del moto delle piccole oscillazioni intorno
da una posizione di equilibrio stabile, si trovano
linearizzando le equazioni del moto.
Questo corrisponde a considerare l'approssimazione quadratica
della lagrangiana intorno alla posizione di equilibrio.
Per Lagrangiane naturali del tipo
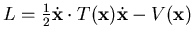 è molto semplice.
Supponiamo che
è molto semplice.
Supponiamo che
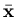 sia la posizione di equilibrio.
Per prima cosa scrivo l'approssimazione quadratica dell'energia
potenziale. La formula di Taylor in più variabili mi dice che
sia la posizione di equilibrio.
Per prima cosa scrivo l'approssimazione quadratica dell'energia
potenziale. La formula di Taylor in più variabili mi dice che
Ora
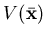 è un valore costante,
dunque posso non scriverlo nella lagrangiana delle piccole oscillazioni.
Il termine al primo ordine è nullo. Infatti
è un valore costante,
dunque posso non scriverlo nella lagrangiana delle piccole oscillazioni.
Il termine al primo ordine è nullo. Infatti
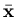 è
una posizione di equilibrio, dunque il gradiente dell'energia potenziale
è nullo.
Il primo termine significativo è
il termine quadratico
è
una posizione di equilibrio, dunque il gradiente dell'energia potenziale
è nullo.
Il primo termine significativo è
il termine quadratico
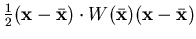 ,
dove con
,
dove con
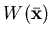 ho indicato la matrice hessiana di
ho indicato la matrice hessiana di 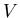 calcolata nel punto di equilibrio
calcolata nel punto di equilibrio
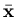 .
I termini successivi sono di ordine superiore, quindi li trascuro.
.
I termini successivi sono di ordine superiore, quindi li trascuro.
La variabile che compirà in questo caso è
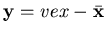 ,
che infatti descrive la posizione rispetto all'equilibrio.
In termini di
,
che infatti descrive la posizione rispetto all'equilibrio.
In termini di
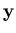 l'approssimazione quadratica dell'energia potenziale
è
l'approssimazione quadratica dell'energia potenziale
è
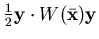 .
L'energia cinetica nella variabile
.
L'energia cinetica nella variabile
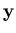 è
è
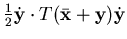 ,
infatti
,
infatti
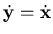 .
Sviluppando
.
Sviluppando 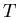 in
in
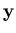 :
:
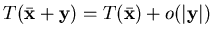 . Ma allora
mi interessa solo l'ordine zero, infatti devo moltiplicare
. Ma allora
mi interessa solo l'ordine zero, infatti devo moltiplicare 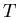 per
per
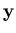 due volte, quindi il termine è già almeno del secondo ordine.
due volte, quindi il termine è già almeno del secondo ordine.
In definitiva:
Esercizio 7.5
Calcola l'Hamiltoniana delle piccole oscillazioni.




Next: 8 Bignamino di Formalismo
Up: Esercitazioni di Meccanica Razionale
Previous: 6.5 Problema
Indice
root
2001-04-02
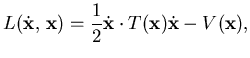
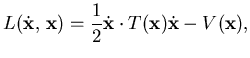
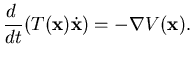
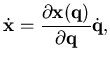
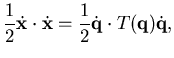
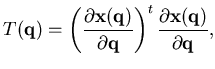
![]() è simmetrica e definita positiva.
è simmetrica e definita positiva.
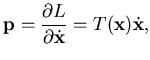
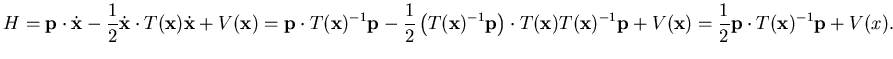
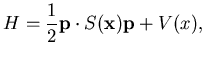
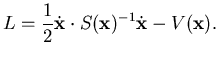
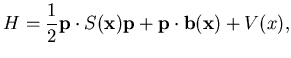
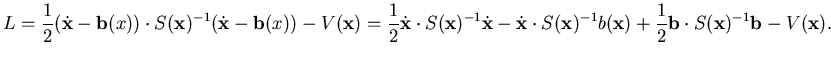
![]() è molto semplice.
Supponiamo che
è molto semplice.
Supponiamo che
![]() sia la posizione di equilibrio.
Per prima cosa scrivo l'approssimazione quadratica dell'energia
potenziale. La formula di Taylor in più variabili mi dice che
sia la posizione di equilibrio.
Per prima cosa scrivo l'approssimazione quadratica dell'energia
potenziale. La formula di Taylor in più variabili mi dice che
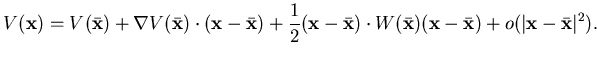
![]() ,
che infatti descrive la posizione rispetto all'equilibrio.
In termini di
,
che infatti descrive la posizione rispetto all'equilibrio.
In termini di
![]() l'approssimazione quadratica dell'energia potenziale
è
l'approssimazione quadratica dell'energia potenziale
è
![]() .
L'energia cinetica nella variabile
.
L'energia cinetica nella variabile
![]() è
è
![]() ,
infatti
,
infatti
![]() .
Sviluppando
.
Sviluppando ![]() in
in
![]() :
:
![]() . Ma allora
mi interessa solo l'ordine zero, infatti devo moltiplicare
. Ma allora
mi interessa solo l'ordine zero, infatti devo moltiplicare ![]() per
per
![]() due volte, quindi il termine è già almeno del secondo ordine.
due volte, quindi il termine è già almeno del secondo ordine.