Considera la successione formata dalle prima cifra dell'espressione
decimale di ![]() :
:
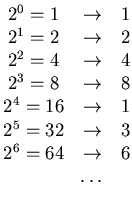
Compare il ![]() nella successione?
nella successione?
Compare più frequentemente il ![]() o l'
o l' ![]() ?
?
Più in generale ![]() può iniziare con una sequenza
arbitraria di cifre?
può iniziare con una sequenza
arbitraria di cifre?
Come si muove un punto materiale soggetto ad una forza di
energia potenziale
![]() con
con ![]() costante?
costante?
Come si muove un punto materiale in presenza
di una parete infinitamente rigida che si muove
con velocità costante ![]() ?
?
Un punto materiale di massa ![]() si muove
tra due pareti infinitamente rigide, la prima fissa
in
si muove
tra due pareti infinitamente rigide, la prima fissa
in ![]() e la seconda in
e la seconda in
![]() , con
, con
![]() .
All'istante iniziale il punto è in
.
All'istante iniziale il punto è in ![]() con velocità
con velocità ![]() . Determina, nel
. Determina, nel
![]() , il
modulo della
velocità del punto nell'istante in cui la barriera mobile
è arrivata in
, il
modulo della
velocità del punto nell'istante in cui la barriera mobile
è arrivata in
![]() .
.
Prova più in generale
che
![]() .
.
Suggerimento: supponi che al tempo ![]() la barriera mobile
sia in
la barriera mobile
sia in ![]() e la particella sia in 0 con velocità
e la particella sia in 0 con velocità ![]() .
Calcola il tempo
.
Calcola il tempo ![]() di ritorno della particella in 0,
la velocità che ha la particella e la posizione della
barriera mobile.
Nota che il prodotto della velocità per la posizione della
barriera al tempo
di ritorno della particella in 0,
la velocità che ha la particella e la posizione della
barriera mobile.
Nota che il prodotto della velocità per la posizione della
barriera al tempo ![]() è identico al prodotto al tempo
è identico al prodotto al tempo ![]() .
Estendi ricorsivamente per i ritorni successivi, e determina
la successione dei tempi di urto con la parete fissa...
.
Estendi ricorsivamente per i ritorni successivi, e determina
la successione dei tempi di urto con la parete fissa...
Osservazione
Fisicamente
![]() ha le dimensioni di una energia per il tempo
(ha le dimensioni dell'azione). Per
ha le dimensioni di una energia per il tempo
(ha le dimensioni dell'azione). Per ![]() costante, l'azione
è proporzionale all'area racchiusa dall'orbita nello spazio
delle fasi (che in questo caso è un rettangolo!).
costante, l'azione
è proporzionale all'area racchiusa dall'orbita nello spazio
delle fasi (che in questo caso è un rettangolo!).
È ovvio che
![]() ,
infatti per
,
infatti per
![]() la barriera è ferma. Questo limite
non è uniforme in
la barriera è ferma. Questo limite
non è uniforme in ![]() .
Dall'esercizio puoi notare che ad un tempo dell'ordine di
.
Dall'esercizio puoi notare che ad un tempo dell'ordine di
![]() la variazione di
la variazione di
![]() rispetto a
rispetto a
![]() è di ordine
è di ordine
![]() .
.
Cioè l'azione è praticamente invariante, rispetto a variazioni lente (adiabatiche) dei parametri fisici che governano il moto.
Per maggiori dettagli vedi l'Arnold [1] e il Landau [9].
L'esercizio precedente ha una interpretazione termodinamica.
È facile identificare l'energia interna:
![]() . È anche facile identificare il `volume':
sarà
. È anche facile identificare il `volume':
sarà ![]() . La pressione è fisicamente la forza esercitata
sull'unità di superficie che racchiude il mezzo.
D'altra parte in questo caso la superficie è un punto
(
. La pressione è fisicamente la forza esercitata
sull'unità di superficie che racchiude il mezzo.
D'altra parte in questo caso la superficie è un punto
(![]() oppure
oppure ![]() ). Se un punto materiale subisce in un certo tempo
). Se un punto materiale subisce in un certo tempo
![]() una variazione di impulso
una variazione di impulso
![]() , la forza
che è stata esercitata su di esso è
, la forza
che è stata esercitata su di esso è
![]() .
Per un urto n
.
Per un urto n ![]() la variazione di impulso è
la variazione di impulso è ![]() .
Nel nostro caso non c'è variazione di impulso
se non quando la massa tocca
.
Nel nostro caso non c'è variazione di impulso
se non quando la massa tocca ![]() .
Per dare senso alla pressione, si può pensare
di considerare l'impulso scambiato con la parete per un tempo
sufficientemente lungo affinché avvengano molti urti,
ma sufficientemente piccolo affinché la variazione dovuta al moto
della barriera mobile non sia significativa (assunzione
possibile se
.
Per dare senso alla pressione, si può pensare
di considerare l'impulso scambiato con la parete per un tempo
sufficientemente lungo affinché avvengano molti urti,
ma sufficientemente piccolo affinché la variazione dovuta al moto
della barriera mobile non sia significativa (assunzione
possibile se
![]() è molto piccolo).
In altre parole:
è molto piccolo).
In altre parole:
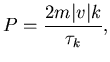
In definitiva, l'interpretazione termodinamica
del moto di una particella tra due pareti perfettamente rigide
a distanza ![]() dà:
dà:
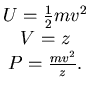
Prova che se ![]() varia molto lentamente,
varia molto lentamente,
Osservazione
Fare la termodinamica di una sola particella è abbastanza privo di senso. Si possono considerare, più correttamente, moltissime particelle tra le pareti, che non urtano tra di loro. Questa situazione può far pensare ad un gas perfetto, per cui la termodinamica ha senso, e la pressione è cinematicamente definita attraverso l'impulso scambiato con le pareti. Tenete presente, però, che un insieme di particelle che non urtano tra loro NON sono un gas perfetto. Infatti manca il meccanismo di termalizzazione tipico, ad esempio, dell'equazione di Boltzmann.
Supponi di avere un moto unidimensionale in cui l'energia totale,
oltre che dipendere dalla posizione e dalla velocità,
dipenda da un parametro ![]() ,
cioè
,
cioè
![]() .
Come esempio puoi pensare a
.
Come esempio puoi pensare a
![]() , dove la massa stessa
è il parametro
, dove la massa stessa
è il parametro ![]() ,
oppure
,
oppure
![]() ,
dove
,
dove ![]() ha le dimensioni di una lunghezza.
ha le dimensioni di una lunghezza.
Supponi, inoltre, che il moto assegnato sia in generle
periodico, ed indica con ![]() la misura dell'area,
nello spazio delle fasi,
della regione racchiusa dall'orbita di energia
la misura dell'area,
nello spazio delle fasi,
della regione racchiusa dall'orbita di energia ![]() .
.
Considera ora il moto con energia totale dipendente
dal tempo attraverso ![]() :
:
![]() , con
, con
![]() piccolo.
piccolo.
Il teorema adiabatico afferma che
In altre parole, per variare l'azione di
![]() devo
aspettare un tempo di ordine
devo
aspettare un tempo di ordine
![]() .
.
In questo enunciato mancano delle ipotesi importanti. Per l'enunciato preciso e per la dimostrazione vedi, tra gli altri, l'Arnold [1]
Considera un pendolo la cui massa diminuisce lentamente con il tempo. Di quanto varia l'ampiezza delle oscillazioni se la massa si dimezza?
Una massa è appesa ad un filo ed oscilla. Se dimezzo lentamente la lunghezza del filo, come cambia l'ampiezza delle oscillazioni?
Considera il moto unidimensionale di energia totale
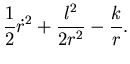
(**) Un satellite in orbita intorno alla Terra descrive un'orbita poco eccentrica. Come cambia l'orbita se il momento della quantità di moto del satellite raddoppia molto lentamente?