



Next: 3 Soluzioni degli esercizi
Up: 2 Moti unidimensionali
Previous: 2.4 Alcuni esercizi chiave
Indice
Subsections
Sia
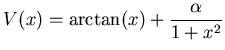 l'energia potenziale
di un moto unidimensionale.
Al variare di
l'energia potenziale
di un moto unidimensionale.
Al variare di
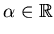 ,
disegnare qualitativamente le orbite nello spazio delle fasi. In particolare
,
disegnare qualitativamente le orbite nello spazio delle fasi. In particolare
- determinare le soluzioni di equilibrio e discuterne la stabilità
- dato
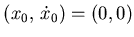 , dato iniziale,
determinare
, dato iniziale,
determinare
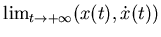
Considerare ora il moto
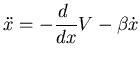 , con
, con 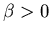 .
Determinare le posizioni di equilibrio e discuterne la stabilità.
.
Determinare le posizioni di equilibrio e discuterne la stabilità.
Per 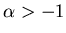 e
e 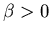 determinare
determinare
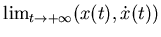 se
se
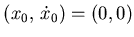 .
.
(*) Risolvere, qualitativamente, il punto precedente nel caso
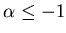 .
.
(*) Sempre nel caso 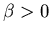 , esiste
, esiste 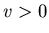 tale che per
il moto di dato iniziale
tale che per
il moto di dato iniziale 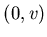 vale
vale
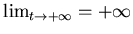 ?
?
Sia
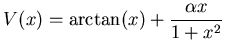 l'energia potenziale
di un moto unidimensionale.
Al variare di
l'energia potenziale
di un moto unidimensionale.
Al variare di
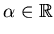 ,
disegnare qualitativamente le orbite nello spazio delle fasi. In particolare
,
disegnare qualitativamente le orbite nello spazio delle fasi. In particolare
- determinare le soluzioni di equilibrio e discuterne la stabilità
- dato
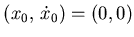 , dato iniziale,
determinare
, dato iniziale,
determinare
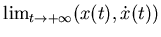
- se
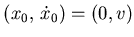 , per quali valori di
, per quali valori di
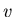 , in funzione di
, in funzione di 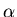 ,
,
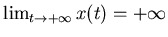 ?
?
Sia
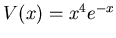 .
l'energia potenziale
di un moto unidimensionale.
Disegnare qualitativamente le orbite nello spazio delle fasi.
In particolare
.
l'energia potenziale
di un moto unidimensionale.
Disegnare qualitativamente le orbite nello spazio delle fasi.
In particolare
- determinare le soluzioni di equilibrio e discuterne la stabilità
- determinare la frequenza delle piccole oscilazioni intorno
alle posizioni di equilibrio stabili
- se
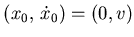 , per quali valori di
, per quali valori di
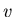 vale
vale
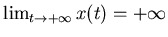 ?
In tal caso;
?
In tal caso;
- quant'è
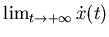 ?
?
- con che velocità, in funzione di
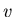 , il punto passa per
, il punto passa per 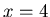 ?
?
- dare l'espressione del tempo che il punto materiale impiega per
arrivare in
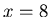 , in funzione di
, in funzione di 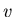 .
.
Sia
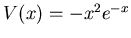 .
l'energia potenziale
di un moto unidimensionale.
Disegnare qualitativamente le orbite nello spazio delle fasi.
In particolare,
.
l'energia potenziale
di un moto unidimensionale.
Disegnare qualitativamente le orbite nello spazio delle fasi.
In particolare,
- calcolare la frequenza delle piccole oscillazioni
intorno alle posizioni di equilibrio stabili
- se
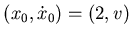 , per quali valori di
, per quali valori di
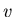 il moto tende a
il moto tende a 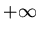 ? E per quali tende a
? E per quali tende a
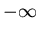 ? In tal caso calcolare in quanto tempo
il punto materiale raggiunge
? In tal caso calcolare in quanto tempo
il punto materiale raggiunge 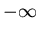 .
.
Sia
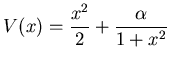 .
l'energia potenziale
di un moto unidimensionale.
Disegnare qualitativamente le orbite nello spazio delle fasi,
al variare di
.
l'energia potenziale
di un moto unidimensionale.
Disegnare qualitativamente le orbite nello spazio delle fasi,
al variare di
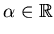 .
In particolare,
.
In particolare,
- determinare le posizioni di equilibrio e discuterne la
stabilità
- per
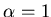 determinare la frequenza delle
piccole oscillazioni intorno alle posizioni di equilibrio stabili
determinare la frequenza delle
piccole oscillazioni intorno alle posizioni di equilibrio stabili
- per
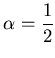 determinare la frequenza delle
piccole oscillazioni intorno alle posizioni di equilibrio stabili
determinare la frequenza delle
piccole oscillazioni intorno alle posizioni di equilibrio stabili
- per
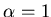 e per il dato iniziale
e per il dato iniziale
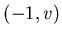 , determinare i valori di
, determinare i valori di 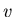 per quali il moto
passa per
per quali il moto
passa per 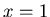 . Dare l'espressione del tempo impiegato,
in funzione di
. Dare l'espressione del tempo impiegato,
in funzione di 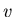 .
.
- con i dati del caso precedente, con che velocità il
punto materiale passa per
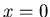 ?
?
- (*) determinare
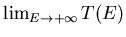 ,
dove
,
dove 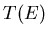 è il periodo del moto di energia
è il periodo del moto di energia 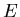 .
.
- (*) sempre per
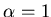 , discutere i valori di
, discutere i valori di 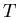 per
i quali esiste un moto periodico di periodo
per
i quali esiste un moto periodico di periodo 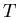 .
.
Sia
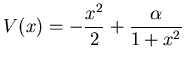 .
l'energia potenziale
di un moto unidimensionale.
Disegnare qualitativamente le orbite nello spazio delle fasi,
al variare di
.
l'energia potenziale
di un moto unidimensionale.
Disegnare qualitativamente le orbite nello spazio delle fasi,
al variare di
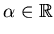 .
In particolare,
.
In particolare,
- determinare le posizioni di equilibrio e discuterne la
stabilità
- per
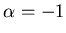 , determinare la frequenza delle piccole
oscillazioni intorno alle posizioni di equilibrio stabili
, determinare la frequenza delle piccole
oscillazioni intorno alle posizioni di equilibrio stabili
- per
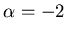 e
e 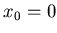 , determinare i valori
della velocità iniziale
, determinare i valori
della velocità iniziale 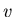 per i quali il moto
è illimitato
per i quali il moto
è illimitato
- nel caso dei dati del punto precedente, se il moto
è illimitato, determinare
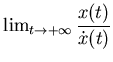 , al variare di
, al variare di 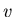
Sia
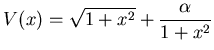 .
l'energia potenziale
di un moto unidimensionale.
Disegnare qualitativamente le orbite nello spazio delle fasi,
al variare di
.
l'energia potenziale
di un moto unidimensionale.
Disegnare qualitativamente le orbite nello spazio delle fasi,
al variare di
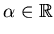 .
In particolare,
.
In particolare,
- determinare le posizioni di equilibrio e discuterne la
stabilità
- determinare la frequenza delle piccole
oscillazioni intorno alle posizioni di equilibrio stabili
- se
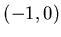 è il dato iniziale, per quali valori di
è il dato iniziale, per quali valori di
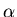 il moto è periodico?
il moto è periodico?
- (*) determinare
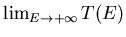 ,
dove
,
dove 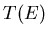 è il periodo del moto di energia
è il periodo del moto di energia 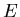 .
.
Sia
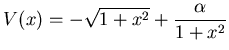 .
l'energia potenziale
di un moto unidimensionale.
Disegnare qualitativamente le orbite nello spazio delle fasi,
al variare di
.
l'energia potenziale
di un moto unidimensionale.
Disegnare qualitativamente le orbite nello spazio delle fasi,
al variare di
 .
In particolare,
.
In particolare,
- determinare le posizioni di equilibrio e discuterne la
stabilità
- determinare la frequenza delle piccole
oscillazioni intorno alle posizioni di equilibrio stabili
- se
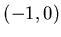 è il dato iniziale, per quali valori di
è il dato iniziale, per quali valori di
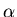 il moto è periodico?
il moto è periodico?
- sia
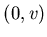 il dato iniziale;
per quali valori di
il dato iniziale;
per quali valori di 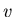 il moto è illimitato?
il moto è illimitato?
- (*) nel caso dei moti illimitati del punto precedente,
determinare
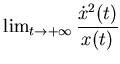 ,
al variare di
,
al variare di 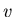 .
.
Sia
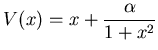 .
l'energia potenziale
di un moto unidimensionale.
Disegnare qualitativamente le orbite nello spazio delle fasi,
al variare di
.
l'energia potenziale
di un moto unidimensionale.
Disegnare qualitativamente le orbite nello spazio delle fasi,
al variare di
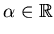 .
In particolare,
.
In particolare,
- determinare le posizioni di equilibrio e discuterne la
stabilità
- determinare la frequenza delle piccole
oscillazioni intorno alle posizioni di equilibrio stabili




Next: 3 Soluzioni degli esercizi
Up: 2 Moti unidimensionali
Previous: 2.4 Alcuni esercizi chiave
Indice
root
2001-04-02
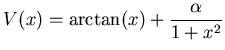 l'energia potenziale
di un moto unidimensionale.
Al variare di
l'energia potenziale
di un moto unidimensionale.
Al variare di
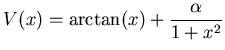 l'energia potenziale
di un moto unidimensionale.
Al variare di
l'energia potenziale
di un moto unidimensionale.
Al variare di
![]() ,
disegnare qualitativamente le orbite nello spazio delle fasi. In particolare
,
disegnare qualitativamente le orbite nello spazio delle fasi. In particolare
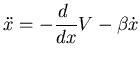 , con
, con ![]() e
e ![]() determinare
determinare
![]() se
se
![]() .
.
![]() .
.
![]() , esiste
, esiste ![]() tale che per
il moto di dato iniziale
tale che per
il moto di dato iniziale ![]() vale
vale
![]() ?
?
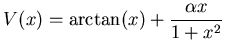 l'energia potenziale
di un moto unidimensionale.
Al variare di
l'energia potenziale
di un moto unidimensionale.
Al variare di
![]() ,
disegnare qualitativamente le orbite nello spazio delle fasi. In particolare
,
disegnare qualitativamente le orbite nello spazio delle fasi. In particolare
![]() .
l'energia potenziale
di un moto unidimensionale.
Disegnare qualitativamente le orbite nello spazio delle fasi.
In particolare
.
l'energia potenziale
di un moto unidimensionale.
Disegnare qualitativamente le orbite nello spazio delle fasi.
In particolare
![]() .
l'energia potenziale
di un moto unidimensionale.
Disegnare qualitativamente le orbite nello spazio delle fasi.
In particolare,
.
l'energia potenziale
di un moto unidimensionale.
Disegnare qualitativamente le orbite nello spazio delle fasi.
In particolare,
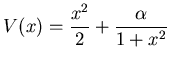 .
l'energia potenziale
di un moto unidimensionale.
Disegnare qualitativamente le orbite nello spazio delle fasi,
al variare di
.
l'energia potenziale
di un moto unidimensionale.
Disegnare qualitativamente le orbite nello spazio delle fasi,
al variare di
![]() .
In particolare,
.
In particolare,
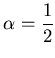 determinare la frequenza delle
piccole oscillazioni intorno alle posizioni di equilibrio stabili
determinare la frequenza delle
piccole oscillazioni intorno alle posizioni di equilibrio stabili
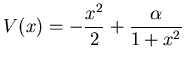 .
l'energia potenziale
di un moto unidimensionale.
Disegnare qualitativamente le orbite nello spazio delle fasi,
al variare di
.
l'energia potenziale
di un moto unidimensionale.
Disegnare qualitativamente le orbite nello spazio delle fasi,
al variare di
![]() .
In particolare,
.
In particolare,
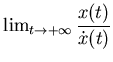 , al variare di
, al variare di 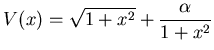 .
l'energia potenziale
di un moto unidimensionale.
Disegnare qualitativamente le orbite nello spazio delle fasi,
al variare di
.
l'energia potenziale
di un moto unidimensionale.
Disegnare qualitativamente le orbite nello spazio delle fasi,
al variare di
![]() .
In particolare,
.
In particolare,
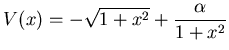 .
l'energia potenziale
di un moto unidimensionale.
Disegnare qualitativamente le orbite nello spazio delle fasi,
al variare di
.
l'energia potenziale
di un moto unidimensionale.
Disegnare qualitativamente le orbite nello spazio delle fasi,
al variare di
![]() .
In particolare,
.
In particolare,
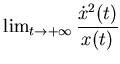 ,
al variare di
,
al variare di 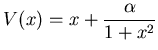 .
l'energia potenziale
di un moto unidimensionale.
Disegnare qualitativamente le orbite nello spazio delle fasi,
al variare di
.
l'energia potenziale
di un moto unidimensionale.
Disegnare qualitativamente le orbite nello spazio delle fasi,
al variare di
![]() .
In particolare,
.
In particolare,