



Next: 2.4 Alcuni esercizi chiave
Up: 2 Moti unidimensionali
Previous: 2.2 Equazioni lineari
Indice
Subsections
2.3 Moti forzati e smorzati
Per le oscillazioni forzate e smorzate mi vengono in mente due testi:
il Landau [9] e il Gallavotti [6].
2.3.1
Risolvi il moto
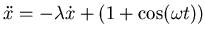 .
Esistono soluzioni stazionarie? Esistono moti periodici?
Esiste
.
Esistono soluzioni stazionarie? Esistono moti periodici?
Esiste
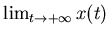 ?
?
2.3.2
Risolvi
con dato iniziale 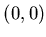 , per
, per
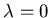 e
e
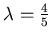 .
.
2.3.3 *
Sia 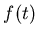 una funzione periodica di periodo
una funzione periodica di periodo
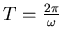 .
Assumi che sia almeno di classe
.
Assumi che sia almeno di classe
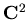 (derivabile due volte
con derivata seconda continua e limitata).
(derivabile due volte
con derivata seconda continua e limitata).
La funzione 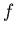 può essere sviluppata in serie di Fourier:
può essere sviluppata in serie di Fourier:
dove
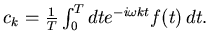 Ricorda che
Ricorda che
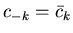 , per la realtà di
, per la realtà di 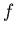 , e
, e
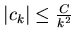 per
per 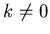 (per l'ipotesi
(per l'ipotesi
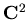 ).
).
Trova per serie una soluzione particolare di
per
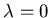 e
e
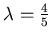 , al variare di
, al variare di
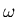 .
Che condizioni devi imporre su
.
Che condizioni devi imporre su 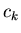 e
e 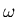 affinché il moto
sia limitato?
affinché il moto
sia limitato?
2.3.4 *
Considera l'oscillatore armonico forzato
Per quali valori di 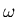 esistono moti periodici?
esistono moti periodici?
Prova che tutti i moti sono periodici se e solo
se
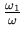 è razionale e diverso da
è razionale e diverso da 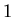 .
.
Prova che se
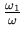 è irrazionale,
il moto nello spazio delle fasi riempie densamente
una regione. Che regione è? (Suggerimento:
vedi l'esercizio 2.4.2)
è irrazionale,
il moto nello spazio delle fasi riempie densamente
una regione. Che regione è? (Suggerimento:
vedi l'esercizio 2.4.2)
2.3.5 *
Considera il moto
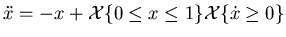 .
.
L'energia meccanica si conserva?
Considera il dato iniziale
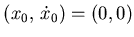 . Risolvi esplicitamente il moto
fino al primo tempo di ritorno del punto materiale in
. Risolvi esplicitamente il moto
fino al primo tempo di ritorno del punto materiale in 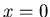 con velocità positiva.
con velocità positiva.
Come avviene il moto fino al secondo ritorno?
E dopo?
Sia 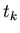 il tempo in cui il punto materiale ritorna in
il tempo in cui il punto materiale ritorna in 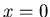 con velocità positiva.
Trova
con velocità positiva.
Trova
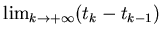 .
.
(Vedi la parte sullo ``scappamento ad ancora'' sul
Gallavotti [6] )




Next: 2.4 Alcuni esercizi chiave
Up: 2 Moti unidimensionali
Previous: 2.2 Equazioni lineari
Indice
root
2001-04-02
![]() può essere sviluppata in serie di Fourier:
può essere sviluppata in serie di Fourier:
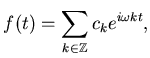
![]() esistono moti periodici?
esistono moti periodici?
![]() è razionale e diverso da
è razionale e diverso da ![]() .
.
![]() è irrazionale,
il moto nello spazio delle fasi riempie densamente
una regione. Che regione è? (Suggerimento:
vedi l'esercizio 2.4.2)
è irrazionale,
il moto nello spazio delle fasi riempie densamente
una regione. Che regione è? (Suggerimento:
vedi l'esercizio 2.4.2)
![]() . Risolvi esplicitamente il moto
fino al primo tempo di ritorno del punto materiale in
. Risolvi esplicitamente il moto
fino al primo tempo di ritorno del punto materiale in ![]() con velocità positiva.
con velocità positiva.
![]() il tempo in cui il punto materiale ritorna in
il tempo in cui il punto materiale ritorna in ![]() con velocità positiva.
Trova
con velocità positiva.
Trova
![]() .
.