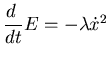 .
Quindi anche in presenza di attrito
.
Quindi anche in presenza di attrito
a)
L'energia è un integrale primo del moto per il sistema
senza attrito.
In presenza di attrito
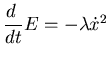 .
Quindi anche in presenza di attrito
.
Quindi anche in presenza di attrito ![]() è una funzione
di Lyapunov per i punti di minimo dell'energia potenziale
è una funzione
di Lyapunov per i punti di minimo dell'energia potenziale
![]() e
e ![]() .
Dunque senz'altro queste due posizioni sono stabili.
Il teorema di Lyapunov, pur decrescendo l'energia, non
permette di concludere immediatamente che
.
Dunque senz'altro queste due posizioni sono stabili.
Il teorema di Lyapunov, pur decrescendo l'energia, non
permette di concludere immediatamente che ![]() e
e ![]() sono
asintoticamente stabili. Infatti
sono
asintoticamente stabili. Infatti
![]() è 0 non solo nella posizione
di equilibrio ma anche in tutti i punti dello spazio delle fasi
in cui
è 0 non solo nella posizione
di equilibrio ma anche in tutti i punti dello spazio delle fasi
in cui
![]() .
Procedo dunque con l'analisi del linearizzato1.
Riscrivo l'equazione del moto come un sistema (non lineare )
del primo ordine.
.
Procedo dunque con l'analisi del linearizzato1.
Riscrivo l'equazione del moto come un sistema (non lineare )
del primo ordine.
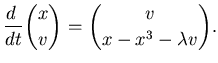
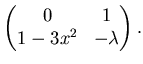
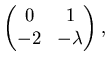
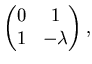
b)
L'energia meccanica non è conservata e decresce nel tempo.
Dunque esiste
![]() (
(![]() è limitata dal basso da
è limitata dal basso da ![]() ).
Dunque il moto, nel limite
).
Dunque il moto, nel limite ![]() che va a infinito,
tende ad avere energia costante. L'idea intuitiva è che
il moto deve tendere ad una soluzione di equilibrio,
se no l'energia continuerebbe a decrescere invece che tendere
al valore
che va a infinito,
tende ad avere energia costante. L'idea intuitiva è che
il moto deve tendere ad una soluzione di equilibrio,
se no l'energia continuerebbe a decrescere invece che tendere
al valore ![]() .
.
L'analisi rigorosa di questo fatto è un po' astratta:
So che l'energia in funzione del tempo ha limite ![]() ,
in particolare
,
in particolare ![]() è limitata.
Ne segue che il moto, nello spazio delle fasi, è limitato.
è limitata.
Ne segue che il moto, nello spazio delle fasi, è limitato.
Sia
![]() un punto di accumulazione per la
traiettoria, cioè esista una sequenza crescente di tempi
un punto di accumulazione per la
traiettoria, cioè esista una sequenza crescente di tempi ![]() ,
con
,
con
![]() per
per
![]() , tale che
, tale che
![]() 2.
Considero adesso, per
2.
Considero adesso, per ![]() assegnato, la successione di
punti dell'orbita
assegnato, la successione di
punti dell'orbita
![]() .
.
L'osservazione importante, a questo punto,
è che la mappa che dà la soluzione al tempo ![]() del
sistema differenziale autonomo che stiamo considerando è
continua nel dato iniziale.
del
sistema differenziale autonomo che stiamo considerando è
continua nel dato iniziale.
In altre parole:
Una dimostrazione più costruttiva è possibile ed istruttiva, anche se più complessa.
Il primo fatto importante è che se ad un certo istante di tempo
![]() il punto è in
il punto è in ![]() con velocità
con velocità ![]() allora
la funzione
allora
la funzione ![]() è invertibile in un intorno di
è invertibile in un intorno di ![]() ,
essendo
,
essendo
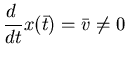 .
Cioè posso pensare il tempo come funzione della posizione,
quindi posso pensare l'energia come funzione della posizione:
.
Cioè posso pensare il tempo come funzione della posizione,
quindi posso pensare l'energia come funzione della posizione:
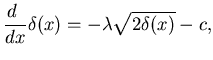
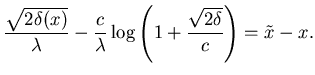
Cosa accade dopo il tempo ![]() ?
Sul punto la forza non è nulla, dunque si muoverà verso
sinistra e di nuovo l'equazione 3.2 descrive
?
Sul punto la forza non è nulla, dunque si muoverà verso
sinistra e di nuovo l'equazione 3.2 descrive ![]() in
funzione di
in
funzione di ![]() . Ripetendo il ragionamento, è evidente che
il punto di ferma solo quando
. Ripetendo il ragionamento, è evidente che
il punto di ferma solo quando ![]() uguaglia
uguaglia ![]() in un punto in cui la
forza è 0, cioè solo se il punto tende ad una posizione di
equilibrio.
in un punto in cui la
forza è 0, cioè solo se il punto tende ad una posizione di
equilibrio.
c)
Nel punto a) ho provato che la soluzione stazionaria ![]() è instabile.
Nonostante ciò esistono traiettorie che tendono a
è instabile.
Nonostante ciò esistono traiettorie che tendono a ![]() .
Un modo per convincersi che è così è quello di
considerare un caso più semplice, cioè il linearizzato intorno
a
.
Un modo per convincersi che è così è quello di
considerare un caso più semplice, cioè il linearizzato intorno
a ![]() .
L'equazione del moto diventa
.
L'equazione del moto diventa
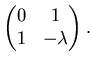
La dimostrazione rigorosa dell'esistenza della varietà stabile nei casi
non lineari è complicata (vedi Dell'Antonio [4]),
comunque qui mi limito a far notare che
si può provare a trovare la soluzione di
3.4 ( che equivale all'equazione 3.2) per
serie.
Nel caso
![]() (esercizio) si ha:
(esercizio) si ha:
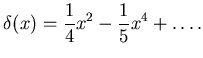
d)
Assunta per buona la figura 2 è facile
capire quali sono i dati iniziali che vengono attratti dalla
posizione ![]() e quali quelli attratti dalla posizione
e quali quelli attratti dalla posizione ![]() .
Infatti la varietà stabile divide il piano delle fasi in due
regioni distinte, una che contiene il punto
.
Infatti la varietà stabile divide il piano delle fasi in due
regioni distinte, una che contiene il punto ![]() , l'altra
che contiene il punto
, l'altra
che contiene il punto ![]() .
.
La figura 2 si giustifica facilmente considerando
che l'energia sulla varietà stabile cresce per
![]() .
Quindi man mano (con il tempo invertito) essa interseca curve
di livello di energia sempre più alta.
Inoltre ognuno dei due rami della varietà stabile incontra
una curva di livello una ed una sola volta, trasversalmente
se
.
Quindi man mano (con il tempo invertito) essa interseca curve
di livello di energia sempre più alta.
Inoltre ognuno dei due rami della varietà stabile incontra
una curva di livello una ed una sola volta, trasversalmente
se
![]() , tangente se
, tangente se ![]() .
.
Una ulteriore domanda che ci si può porre,
è di quanto aumenta l'energia ogni volta che il
punto passa per la posizione ![]() , mandando il tempo a
, mandando il tempo a ![]() .
Tornando alla figura 1, e indicando con
.
Tornando alla figura 1, e indicando con ![]() il valore
dell'energia nel punto
il valore
dell'energia nel punto ![]() dove il moto inverte la
velocità:
dove il moto inverte la
velocità:
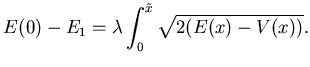
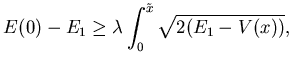
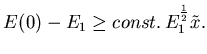
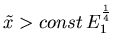 .
In definitiva
.
In definitiva
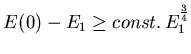 .
Il che significa che man mano che mi allontano da
.
Il che significa che man mano che mi allontano da
Nella figura 3.4.1 ho disegnato la curva ![]() per
il ramo della varietà stabile che arriva nell'origine con velocità
negativa.
A quale posizione di equilibrio tende il moto
che parte con velocità positiva, energia
per
il ramo della varietà stabile che arriva nell'origine con velocità
negativa.
A quale posizione di equilibrio tende il moto
che parte con velocità positiva, energia ![]() e posizione
iniziale nulla?
e posizione
iniziale nulla?