



Next: 2.2 Equazioni lineari
Up: 2 Moti unidimensionali
Previous: 2 Moti unidimensionali
Indice
Subsections
2.1 Esercizi sui moti unidimensionali
Sono trattati in tutti i libri di meccanica. Un'esposizione molto chiara
è sull'Olivieri [10].
2.1.1
Calcola il periodo delle oscillazioni del moto unidimensionale di
energia potenziale
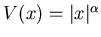 , per
, per
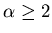 , in
funzione dell'energia (vedi Landau [9]).
, in
funzione dell'energia (vedi Landau [9]).
Soluzione
2.1.2
Considera il moto unidimensionale
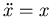 . Trova il moto
con dato iniziale
. Trova il moto
con dato iniziale
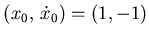 . In quanto tempo
la traiettoria arriva in
. In quanto tempo
la traiettoria arriva in 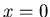 ?
?
Trova tutti i dati iniziali tali che
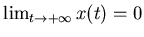 .
.
Trova tutti i dati iniziali tali che
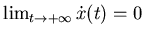 .
.
Soluzione
2.1.3 La doppia buca di potenziale
Considera il moto di un punto materiale di
massa 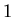 nella ``doppia buca di potenziale''
nella ``doppia buca di potenziale''
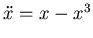 .
.
Disegna le orbite nello spazio delle fasi.
Discuti la stabilità delle posizioni di equilibrio.
Determina il numero delle orbite ad energia 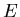 , al variare di
, al variare di 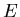 .
.
Considera il dato iniziale
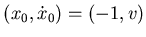 ;
per quali valori di
;
per quali valori di
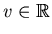 il punto materiale raggiunge la posizione
il punto materiale raggiunge la posizione
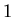 ?
?
Con che velocità ci arriva?
Per 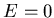 il moto avviene sulla ``separatrice''. Con che angolo
la separatrice interseca gli assi?
il moto avviene sulla ``separatrice''. Con che angolo
la separatrice interseca gli assi?
Soluzione
2.1.4 La doppia buca parte II
Considera il moto di un punto materiale di
massa 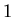 di energia potenziale
di energia potenziale
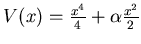 ,
con
,
con
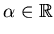 .
.
Discuti qualitativamente il moto al variare di 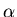
In paricolare determina le posizioni di equilibrio
e la loro stabilità al variare di 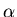 .
.
Disegna il grafico delle posizioni di equilibrio
al variare di 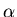 .
.
Soluzione
2.1.5
Considera il moto di un punto materiale di massa 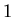 di energia potenziale
di energia potenziale
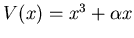 ,
con
,
con
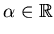 .
.
Discuti qualitativamente il moto al variare di 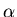
In paricolare determina le posizioni di equilibrio
e la loro stabilità al variare di 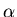 .
.
Disegna il grafico delle posizioni di equilibrio
al variare di 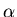 .
.
Soluzione
2.1.6 Variante della doppia buca
Considera il moto di un punto materiale di massa 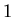 , soggetto ad una
forza
di energia potenziale
, soggetto ad una
forza
di energia potenziale
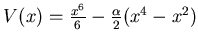 ,
con
,
con
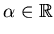 .
.
Discuti qualitativamente il moto al variare di 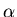
In paricolare determina le posizioni di equilibrio
e la loro stabilità al variare di 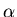 .
.
Disegna il grafico delle posizioni di equilibrio
al variare di 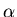 .
.
Soluzione
2.1.7 Il pendolo su un piano ruotante
Considera il moto
dove 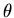 è un angolo,
è un angolo, 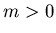 la massa,
la massa, 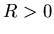 una lunghezza,
una lunghezza,
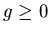 un'accelerazione e
un'accelerazione e
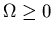 una frequenza.
Questa equazione descrive un pendolo, cioè un punto
materiale di massa
una frequenza.
Questa equazione descrive un pendolo, cioè un punto
materiale di massa
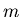 su un estremo di un'asta di lunghezza
su un estremo di un'asta di lunghezza 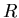 con l'altro estremo fissato, soggetta alla forza
di gravità, su di un piano
verticale che ruota con velocità costante di frequenza
con l'altro estremo fissato, soggetta alla forza
di gravità, su di un piano
verticale che ruota con velocità costante di frequenza 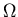 .
L'angolo
.
L'angolo 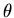 è misurato dala verticale. Quando
è misurato dala verticale. Quando 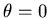 il punto materiale si trova nella posizione di minima altezza.
il punto materiale si trova nella posizione di minima altezza.
Discuti qualitativamente il moto.
In particolare studia l'esistenza e la stabilità delle
posizioni di equilibrio
al variare del parametro
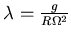 .
Che dimensioni fisiche ha
.
Che dimensioni fisiche ha 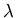 ?
Disegna il grafico delle posizioni di equilibrio al
variare di
?
Disegna il grafico delle posizioni di equilibrio al
variare di 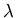 .
(Vedi Dell'Antonio [5]).
.
(Vedi Dell'Antonio [5]).
Considera il dato iniziale
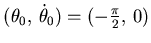 .
.
Prova che il moto è periodico e scrivi il periodo dell'orbita.
In quanto tempo il pendolo arriva in
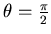 ?
?
Con che
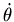 ci arriva?
ci arriva?
Quanto vale
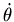 quando il pendolo passa per
quando il pendolo passa per 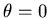 ?
?
Quant'è il valore massimo che
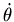 assume?
assume?
Per quali istanti di tempo
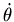 raggiunge il massimo?
raggiunge il massimo?
Quanto vale 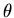 quando
quando
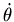 è massimo?
è massimo?
Considera il dato iniziale
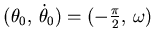 ,
con
,
con 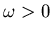 .
.
Per quali valori di 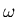 il pendolo ha un moto periodico?
il pendolo ha un moto periodico?
Esprimi per tali valori il periodo del moto.
Determina l'andamento asintotico del periodo per
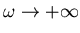 .
.
La componente verticale della reazione vincolare è:
Reazione
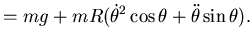
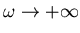 ,
quando il pendolo è in
,
quando il pendolo è in
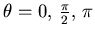 .
.
Soluzione
2.1.8
Considera il moto di un punto materiale di massa 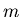 ,
di energia potenziale
dove
,
di energia potenziale
dove
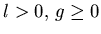 hanno, rispettivamente,
le dimensioni di una lunghezza e di una accelerazione, e
hanno, rispettivamente,
le dimensioni di una lunghezza e di una accelerazione, e
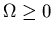 ha le dimensioni di una frequenza.
Nota che gli aspetti qualitativi del moto
dipendono dai parametri fisici
ha le dimensioni di una frequenza.
Nota che gli aspetti qualitativi del moto
dipendono dai parametri fisici
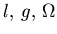 attraverso
un unico parametro adimensionale.
Discuti qualitativamente il moto, in particolare
l'esistenza delle posizioni di equilibrio e la loro stabilità.
attraverso
un unico parametro adimensionale.
Discuti qualitativamente il moto, in particolare
l'esistenza delle posizioni di equilibrio e la loro stabilità.
Soluzione
2.1.9
Considera il moto di un punto materiale di massa 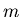 ,
di energia potenziale
dove
,
di energia potenziale
dove
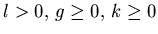 , hanno, rispettivamente,
le dimensioni di una lunghezza, di una accelerazione e di
una costante di elasticità.
Nota che gli aspetti qualitativi del moto
dipendono dai parametri fisici
, hanno, rispettivamente,
le dimensioni di una lunghezza, di una accelerazione e di
una costante di elasticità.
Nota che gli aspetti qualitativi del moto
dipendono dai parametri fisici
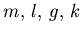 attraverso
un unico parametro adimensionale.
Discuti qualitativamente il moto, in particolare
l'esistenza delle posizioni di equilibrio e la loro stabilità.
attraverso
un unico parametro adimensionale.
Discuti qualitativamente il moto, in particolare
l'esistenza delle posizioni di equilibrio e la loro stabilità.
Soluzione
2.1.10
Un punto materiale di massa 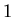 si muove su una retta sotto l'azione
di una forza di energia potenziale
si muove su una retta sotto l'azione
di una forza di energia potenziale
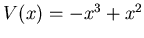 .
Considera i dati iniziali di energia totale
.
Considera i dati iniziali di energia totale
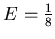 , e sia
, e sia
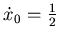 . Determina i valori di
. Determina i valori di 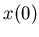 per i quali il moto è
periodico e dai un'espressione del periodo.
Soluzione
per i quali il moto è
periodico e dai un'espressione del periodo.
Soluzione
2.1.11
Un punto materiale di massa 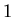 si muove su una retta sotto l'azione
di una forza di energia potenziale
si muove su una retta sotto l'azione
di una forza di energia potenziale
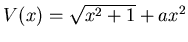 ,
con
,
con
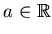 .
.
Per quali valori di 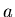 tutte le orbite sono limitate?
tutte le orbite sono limitate?
Per quali valori di 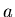 l'origine è stabile?
l'origine è stabile?
Risposta
2.1.12 *
Un punto materiale di massa 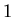 , su una retta, inizialmente
in
, su una retta, inizialmente
in 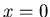 con velocità
con velocità
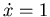 ,
si muove sotto l'azione
di una forza di energia potenziale
,
si muove sotto l'azione
di una forza di energia potenziale
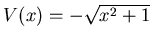 .
.
Prova che il moto è illimitato.
Prova che esiste un'accelerazione asintotica
(cioè
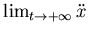 è finito)
è finito)
Prova che asintoticamente nel tempo il moto tende
ad un moto uniformemente accelerato.
In altri termini esistono 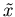 ,
, 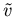 , e
, e 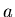 tali che
tali che
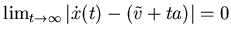 e
e
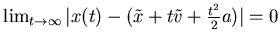 .
.
Soluzione
2.1.13
Un punto materiale di massa 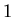 si muove sulla semiretta
si muove sulla semiretta 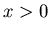 soggetto ad una forza di energia potenziale
soggetto ad una forza di energia potenziale
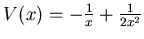 .
.
Per quali dati iniziali il moto è periodico?
Per quali dati iniziali il moto non è periodico?
Per quali dati iniziali il moto è illimitato?
Quali solo le soluzioni stazionarie?
Sia
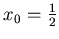 e
e
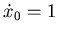 . Determina
. Determina
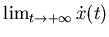 .
.
Sia
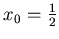 e
e
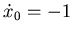 .
Qual è il massimo della velocità che il punto raggiuge?
E qual è il minima?
.
Qual è il massimo della velocità che il punto raggiuge?
E qual è il minima?
Risposta
2.1.14 *
Sia
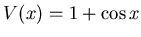 per
per
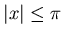 , e
, e 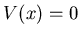 per
per
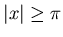 .
.
Discuti qualitativamente il moto.
Discuti qualitativamente il moto per il potenziale
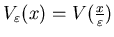 con
con
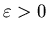 ; cosa accade nel limite
; cosa accade nel limite
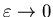 ?
?
Discuti qualitativamente il moto per il potenziale
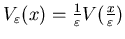 con
con
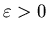 ; cosa accade nel limite
; cosa accade nel limite
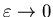 ?
?
Qual è il moto di una particella che rimbalza
contro un ``muro infinitamente rigido''?
Soluzione
2.1.15 *
Sia
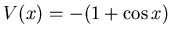 per
per
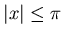 , e
, e 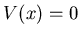 per
per
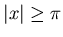 .
.
Discuti qualitativamente il moto.
Discuti qualitativamente il moto per il potenziale
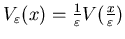 con
con
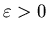 , per dati iniziali di
energia totale positiva. Cosa accade nel limite
, per dati iniziali di
energia totale positiva. Cosa accade nel limite
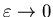 ?
?
Soluzione
2.1.16
Sia 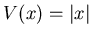 .
Discuti qualitativamente il moto.
Quant'è la forza in
.
Discuti qualitativamente il moto.
Quant'è la forza in 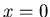 ?
Sia
?
Sia 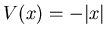 . Trova il moto di dato iniziale
. Trova il moto di dato iniziale
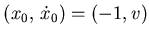 al variare di
al variare di 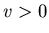 .
Considera ora
.
Considera ora
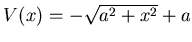 , con
, con 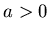 .
Determina il moto di dato iniziale
.
Determina il moto di dato iniziale
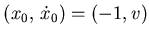 al variare di
al variare di 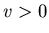 , e il limite di tale moto per
, e il limite di tale moto per 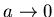 .
.
Soluzione
2.1.17 *
Sia
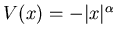 con
con 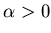 . Considera
il dato iniziale
. Considera
il dato iniziale
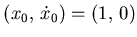 .
In quanto tempo il punto materiale raggiunge
.
In quanto tempo il punto materiale raggiunge 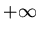 ?
Per quanto tempo il moto esiste?
?
Per quanto tempo il moto esiste?
Sia 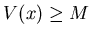 per ogni
per ogni 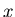 reale. Prova che
reale. Prova che
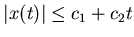 , per
, per
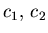 costanti opportune
che dipendono dal dato iniziale.
Prova che il moto esiste per tutti i tempi.
costanti opportune
che dipendono dal dato iniziale.
Prova che il moto esiste per tutti i tempi.
Soluzione
2.1.18
Sia
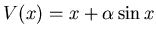 , con
, con
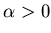 .
Discuti qualitativamente il moto al variare di
.
Discuti qualitativamente il moto al variare di 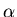 .
In particolare trova gli
.
In particolare trova gli 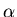 per cui esistono
soluzioni stazionarie e discutine la stabilità.
Determina per quali
per cui esistono
soluzioni stazionarie e discutine la stabilità.
Determina per quali 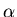 esistono orbite
periodiche.
esistono orbite
periodiche.
Soluzione
2.1.19 *
Sia
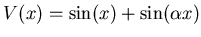 , con
, con
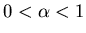 , e
, e
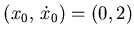 .
Determina
.
Determina
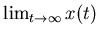 al variare di
al variare di 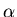 .
(Suggerimento:
vedi l'esercizio sul ritorno)
.
(Suggerimento:
vedi l'esercizio sul ritorno)
Soluzione
2.1.20
Sia
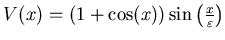 , e
, e
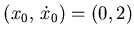 .
Per quali valori di
.
Per quali valori di
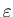 il moto è illimitato?
Soluzione
il moto è illimitato?
Soluzione
2.1.21 **
Sia
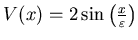 ,
, 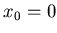 e
e
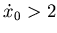 .
Determina il tempo necessario per raggiungere
.
Determina il tempo necessario per raggiungere 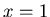 , nel limite
, nel limite
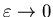 .
Soluzione
.
Soluzione
2.1.22 ***
Sia
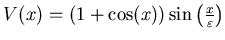 , e
, e
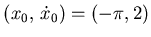 .
Indica con
.
Indica con
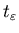 il tempo necessario per raggiungere
il tempo necessario per raggiungere
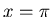 .
Prova che
.
Prova che
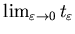 è finito.
Sia
è finito.
Sia
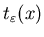 il tempo necessario per raggiungere
il tempo necessario per raggiungere
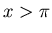 .
Prova che
.
Prova che
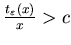 per ogni
per ogni
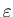 ed ogni
ed ogni 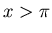
Soluzione
2.1.23 Domande brevi
- a)
- In generale un'orbita periodica è descritta da
un'ellisse nello spazio delle fasi?
- b)
- Sia
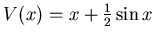 . Quant'è
. Quant'è
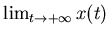 ?
Il moto è uniformemente accelerato?
?
Il moto è uniformemente accelerato?
- c)
- Come è la parte reale degli autovalori
di un sistema conservativo linearizzato intorno ad una posizione di equilibrio
stabile?
- d)
- Discuti la stabilità dell'origine per le
seguenti equazioni differenziali:
- 1.
-
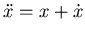
- 2.
-
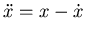
- 3.
-
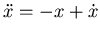
- 4.
-
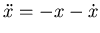
Quale di esse descrive
un oscillatore armonico con attrito a tempo invertito?
E quale il linearizzato di un pendolo capovolto
con attrito?
- e)
- Per quali dei seguenti moti unidimensionali
l'energia meccanica è conservata?
- 1.
-
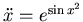
- 2.
-
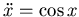
- 3.
-
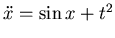
- 4.
-
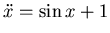
- 5.
-
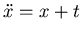
- 6.
-
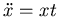
- 7.
-
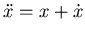
- 8.
-
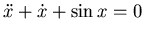
- 9.
-
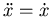
- 10.
-
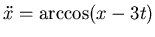
In due degli esempi precedenti, anche se l'energia meccanica
non si conserva, c'è un integrale primo del moto,
dipendente dal tempo, che ne permette
l'analisi qualitativa. Quali sono? Qual è l'interpretazione
fisica di tali integrali primi? (vedi l'inizio dell'esercizio
2.4.5).
Soluzione




Next: 2.2 Equazioni lineari
Up: 2 Moti unidimensionali
Previous: 2 Moti unidimensionali
Indice
root
2001-04-02
![]() .
.
![]() .
.
![]() , al variare di
, al variare di ![]() .
.
![]() ;
per quali valori di
;
per quali valori di
![]() il punto materiale raggiunge la posizione
il punto materiale raggiunge la posizione
![]() ?
?
![]() il moto avviene sulla ``separatrice''. Con che angolo
la separatrice interseca gli assi?
il moto avviene sulla ``separatrice''. Con che angolo
la separatrice interseca gli assi?
![]()
![]() .
.
![]() .
.
![]()
![]() .
.
![]() .
.
![]()
![]() .
.
![]() .
.
![]() .
Che dimensioni fisiche ha
.
Che dimensioni fisiche ha ![]() ?
Disegna il grafico delle posizioni di equilibrio al
variare di
?
Disegna il grafico delle posizioni di equilibrio al
variare di ![]() .
(Vedi Dell'Antonio [5]).
.
(Vedi Dell'Antonio [5]).
![]() .
.
![]() ?
?
![]() ci arriva?
ci arriva?
![]() quando il pendolo passa per
quando il pendolo passa per ![]() ?
?
![]() assume?
assume?
![]() raggiunge il massimo?
raggiunge il massimo?
![]() quando
quando
![]() è massimo?
è massimo?
![]() ,
con
,
con ![]() .
.
![]() il pendolo ha un moto periodico?
il pendolo ha un moto periodico?
![]() .
.
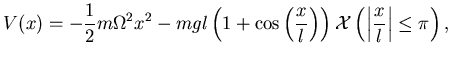
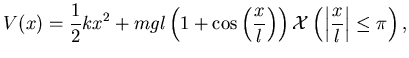
![]() tutte le orbite sono limitate?
tutte le orbite sono limitate?
![]() l'origine è stabile?
l'origine è stabile?
![]() è finito)
è finito)
![]() ,
, ![]() , e
, e ![]() tali che
tali che
![]() e
e
![]() .
.
![]() e
e
![]() . Determina
. Determina
![]() .
.
![]() e
e
![]() .
Qual è il massimo della velocità che il punto raggiuge?
E qual è il minima?
.
Qual è il massimo della velocità che il punto raggiuge?
E qual è il minima?
![]() con
con
![]() ; cosa accade nel limite
; cosa accade nel limite
![]() ?
?
![]() con
con
![]() ; cosa accade nel limite
; cosa accade nel limite
![]() ?
?
![]() con
con
![]() , per dati iniziali di
energia totale positiva. Cosa accade nel limite
, per dati iniziali di
energia totale positiva. Cosa accade nel limite
![]() ?
?
![]() con
con ![]() . Considera
il dato iniziale
. Considera
il dato iniziale
![]() .
In quanto tempo il punto materiale raggiunge
.
In quanto tempo il punto materiale raggiunge ![]() ?
Per quanto tempo il moto esiste?
?
Per quanto tempo il moto esiste?
![]() per ogni
per ogni ![]() reale. Prova che
reale. Prova che
![]() , per
, per
![]() costanti opportune
che dipendono dal dato iniziale.
Prova che il moto esiste per tutti i tempi.
costanti opportune
che dipendono dal dato iniziale.
Prova che il moto esiste per tutti i tempi.