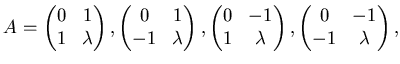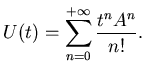Next: 2.3 Moti forzati e
Up: 2 Moti unidimensionali
Previous: 2.1 Esercizi sui moti
Indice
Subsections
2.2 Equazioni lineari
Nei testi di analisi matematica l'aspetto qualitativo
è tipicamente sottorappresentato.
Vedi invece i testi di Arnold
[1,2] e in generale i libri di Meccanica.
2.2.1
Linearizza l'equazione del pendolo
intorno a tutte le posizioni di equilibrio.
2.2.2
Descrivi le traiettorie nello spazio delle fasi di
per
al variare di
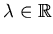 (anche negativo).
(anche negativo).
2.2.3
Che relazione devono verificare la matrice 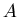 e il vettore
e il vettore
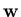 affinché
il sistema
ammetta una soluzione periodica di periodo
affinché
il sistema
ammetta una soluzione periodica di periodo 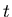 ?
(Suggerimento: cerca soluzioni del tipo
?
(Suggerimento: cerca soluzioni del tipo
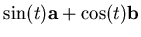 ).
).
2.2.4 *
Considera il sistema lineare
con dato iniziale
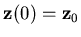 .
Prova che la soluzione è lineare nel dato iniziale.
Questo implica che esiste una matrice
.
Prova che la soluzione è lineare nel dato iniziale.
Questo implica che esiste una matrice 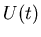 tale che
tale che
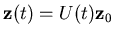 .
Prova che la matrice
.
Prova che la matrice 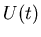 può essere ottenuta
come somma della serie di matrici:
Per questo motivo
può essere ottenuta
come somma della serie di matrici:
Per questo motivo 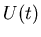 si indica spesso con
si indica spesso con 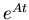 .
(Suggerimento: lo spazio delle matrici con la norma
.
(Suggerimento: lo spazio delle matrici con la norma
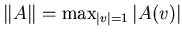 è completo e vale
è completo e vale
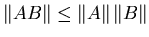 . La serie è una serie di potenze
in
. La serie è una serie di potenze
in 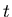 quindi ha un raggio di convergenza, determinalo e deriva
termine a termine).
quindi ha un raggio di convergenza, determinalo e deriva
termine a termine).




Next: 2.3 Moti forzati e
Up: 2 Moti unidimensionali
Previous: 2.1 Esercizi sui moti
Indice
root
2001-04-02