L'energia potenziale è una funzione simmetrica rispetto all'asse
delle ![]() . Dunque
. Dunque
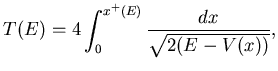 |
(3.1) |
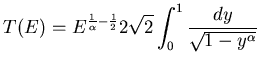
Dal ritratto di fase si deduce facilmente che la traiettoria
di dato iniziale
![]() passa per
passa per ![]() se e solo se
l'energia totale è maggiore di 0, che è il valore
del massimo locale di
se e solo se
l'energia totale è maggiore di 0, che è il valore
del massimo locale di ![]() .
Dunque
.
Dunque
![]() ,
cioè
,
cioè
![]() .
Il valore di
.
Il valore di ![]() in
in ![]() e
e ![]() è identico;
dunque per la conservazione dell'energia, anche il valore
di
è identico;
dunque per la conservazione dell'energia, anche il valore
di ![]() è identico.
Quindi,
al primo passaggio per
è identico.
Quindi,
al primo passaggio per ![]() , la velocità è
, la velocità è
![]() .
.
Nel ritratto dell'orbita nello spazio delle fasi,
la curva di energia ![]() è descritta da
è descritta da
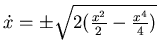 .
La tangente dell'angolo richiesto è
.
La tangente dell'angolo richiesto è
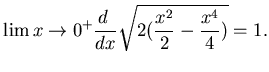
Per
![]() , il moto è qualitativamente uguale al caso
, il moto è qualitativamente uguale al caso
![]() ,
descritto nell'esercizio precedente.
,
descritto nell'esercizio precedente.
Per
![]() , l'energia potenziale è strettamente convessa;
l'unica posizione di equilibrio è
, l'energia potenziale è strettamente convessa;
l'unica posizione di equilibrio è ![]() , ed è stabile.
In particolare per
, ed è stabile.
In particolare per
![]() esiste la frequenza delle
piccole oscillazioni, per
esiste la frequenza delle
piccole oscillazioni, per
![]() non esiste
(vedi esercizio 2.1.1).
non esiste
(vedi esercizio 2.1.1).
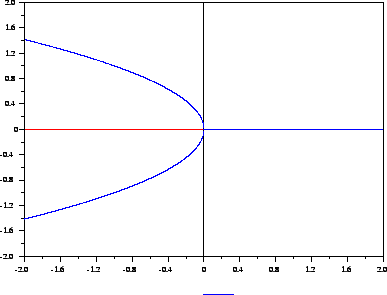
Nella figura, in ascissa cè i valore di ![]() ,
le curve rosse e blu sono le ascisse delle posizioni di equilibrio,
in rosso se l'equilibrio è instabile, in blu se è stabile.
La poszione
,
le curve rosse e blu sono le ascisse delle posizioni di equilibrio,
in rosso se l'equilibrio è instabile, in blu se è stabile.
La poszione ![]() è stabile per
è stabile per
![]() ,
instabile per
,
instabile per ![]() .
Le altre posizioni di equilibrio esistono solo per
.
Le altre posizioni di equilibrio esistono solo per ![]() e
sono stabili.
e
sono stabili.
Per
![]() l'energia potenziale è monotona strettamente crescente.
Non esistono posizioni di equilibrio, le orbite sono tutte illimitate,
Per tutti i dati iniziali
l'energia potenziale è monotona strettamente crescente.
Non esistono posizioni di equilibrio, le orbite sono tutte illimitate,
Per tutti i dati iniziali ![]() tende a
tende a ![]() .
Il tempo che impiega la particella per raggiungere
.
Il tempo che impiega la particella per raggiungere
![]() è finito,
infatti
è finito,
infatti
![]() .
.
Per
![]() cè la posizione di equilibrio
cè la posizione di equilibrio ![]() .
Tutte le altre orbite sono illimitate come nel caso
precedente. La posizione di equilibrio è instabile,
essendo un punto di flesso.
.
Tutte le altre orbite sono illimitate come nel caso
precedente. La posizione di equilibrio è instabile,
essendo un punto di flesso.
Per
![]() ci sono due posizioni di equilibrio:
ci sono due posizioni di equilibrio:
![]() . La posiozione
. La posiozione ![]() è instabile
(massimo locale di
è instabile
(massimo locale di ![]() ),
la posizione
),
la posizione ![]() è stabile (minino locale di
è stabile (minino locale di ![]() ).
Il valore di
).
Il valore di ![]() nei punti di equilibrio è
nei punti di equilibrio è
![]() .
Per
.
Per ![]() cè solo un' orbita illimitata.
Per
cè solo un' orbita illimitata.
Per ![]() un'orbita illimita e
un'orbita illimita e ![]() equilibrio stabile.
Per
equilibrio stabile.
Per
![]() un'orbita illimitata e una periodica.
Per
un'orbita illimitata e una periodica.
Per ![]() la posizione di equilibrio instabile
la posizione di equilibrio instabile ![]() ,
un'orbita limitata a meta asintotica nella regione
,
un'orbita limitata a meta asintotica nella regione
![]() , un'orbita illimitata a meta asintotica nel passato
nella regione
, un'orbita illimitata a meta asintotica nel passato
nella regione ![]() ,
,
![]() ,
un'orbita illimitata a meta asintotica nel futuro
nella regione
,
un'orbita illimitata a meta asintotica nel futuro
nella regione ![]() ,
,
![]() .
.

La derivata è
![]() .
Dunque
.
Dunque ![]() è soluzione di equilibrio per tutti i valori di
è soluzione di equilibrio per tutti i valori di
![]() .
Le altre eventuali posizioni di equilibrio verificano
.
Le altre eventuali posizioni di equilibrio verificano
![]() .
Condizione necessaria affinché esistano è che
.
Condizione necessaria affinché esistano è che
![]() cioè
cioè
![]() o
o
![]() .
Per
.
Per
![]() ,
,
![]() ,
dunque
esistono quattro posizioni di equilibrio:
,
dunque
esistono quattro posizioni di equilibrio:
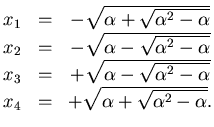
In sintesi:
![]() : due posizioni di equilibrio stabili
: due posizioni di equilibrio stabili ![]() e
e ![]() ,
ed una instabile
,
ed una instabile ![]() ;
;
![]() : una sola posizione di equilibrio
: una sola posizione di equilibrio ![]() stabile.
stabile.
![]() : tre posizioni di equilibrio stabili
: tre posizioni di equilibrio stabili ![]() ,
, ![]() e
e ![]() ,
e due instabili
,
e due instabili ![]() e
e ![]() .
.
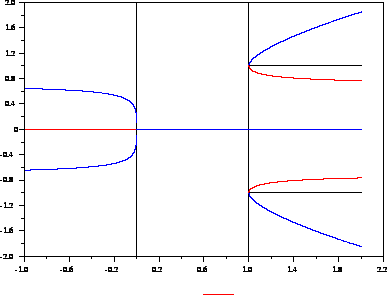
Il dato iniziale
![]() ha energia totale 0.
I livelli critici dell'energia sono:
ha energia totale 0.
I livelli critici dell'energia sono:
per
![]() :
:
![]() (livello di minimo,
(livello di minimo, ![]() ) e
) e
![]() (livello di massimo,
(livello di massimo,
![]() ).
).
per
![]() :
: ![]() diventa un livello di massimo locale,
il livello di minimo è
diventa un livello di massimo locale,
il livello di minimo è
![]() , che
corrisponde alle due soluzioni stazionarie
, che
corrisponde alle due soluzioni stazionarie
![]() .
.
Dunqye ![]() è un livello critico solo se coincide con
è un livello critico solo se coincide con ![]() ,
il che accade se
,
il che accade se
![]() ; in tal caso, essendo
; in tal caso, essendo
![]() , l'orbita è periodica.
Il periodo è:
, l'orbita è periodica.
Il periodo è:
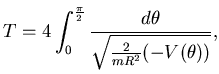
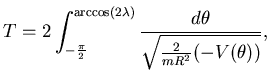
La posizione
![]() è raggiunta solo se
è raggiunta solo se
![]() ;
il tempoè:
;
il tempoè:
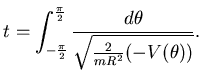
Sempre per la conservazione dell'energia,
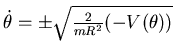 ,
dunque quando
,
dunque quando
![]() ,
,
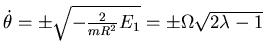 .
.
Il valore del massimo
![]() è raggiunto quando, lungo
l'orbita,
è raggiunto quando, lungo
l'orbita, ![]() è minimo.
Se
è minimo.
Se
![]() il minimo è raggiunto in
il minimo è raggiunto in
![]() ;
se
;
se
![]() , il minimo è raggiunto in
, il minimo è raggiunto in
![]() .
.
Il dato iniziale
![]() ha energia totale
ha energia totale
![]() ;
per
;
per ![]() grande, l'orbita è periodica perché
la variabile è un angolo. Il moto è la rotazione completa.
Il periodo è
grande, l'orbita è periodica perché
la variabile è un angolo. Il moto è la rotazione completa.
Il periodo è
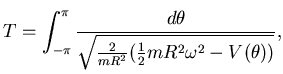
Nelle posizioni di equilibrio
![]() e
e
![]() ,
l'accelerazione è nulla
,
l'accelerazione è nulla
![]() ,
dunque per
,
dunque per ![]() grande la va come
grande la va come ![]() in
in
![]() e
e
![]() in
in
![]() .
.
Per
![]() , il coseno è nullo, e
dall'equazione del moto ricavo
, il coseno è nullo, e
dall'equazione del moto ricavo
![]() , cioè
, cioè
![]() .
Ne segue che la componente verticale della reazione è nulla.
.
Ne segue che la componente verticale della reazione è nulla.
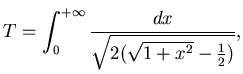
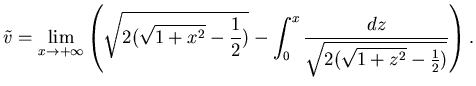
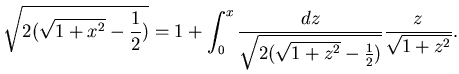
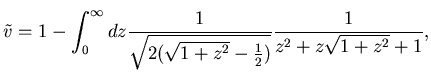
Per
![]() e
e
![]() l'energia vale
l'energia vale ![]() .
che è positiva. Dunque
.
che è positiva. Dunque
![]() .
Il valore asintotico della velocità è
.
Il valore asintotico della velocità è
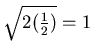 .
.
Per
![]() e
e
![]() , il punto si muove verso sinistra
diminuendo il valore assoluto della sua velocità. Successivamente
inverte la velocità.
Dunque il minimo della velocità è
, il punto si muove verso sinistra
diminuendo il valore assoluto della sua velocità. Successivamente
inverte la velocità.
Dunque il minimo della velocità è ![]() , quella del dato iniziale.
Il massimo è raggiunto in
, quella del dato iniziale.
Il massimo è raggiunto in ![]() (che è il minimo dell'energia potenziale), e vale
(che è il minimo dell'energia potenziale), e vale
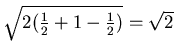 .
.
a) No, solo se il potenziale è armonico.
b) Il limite è ![]() , e il moto NON è uniformemente accelerato.
, e il moto NON è uniformemente accelerato.
c) nulla
d) Solo nel caso 4 l'origine è stabile. Il pendolo capovolto linearizzato con attrito è il caso 2. Il caso 3 è un oscillatore armonico con attrito a tempo invertito.
e) 1, 2. I casi 5 e 10 possono considerarsi come moti unidimensionale visti in un sistema di riferimento mobile, di velocità costante. L'energia nel sistema solidale si conserva.