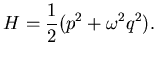
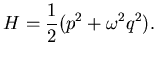
La variabile d'azione è:
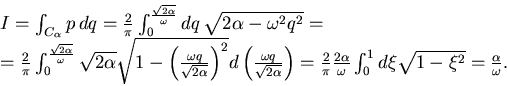 |
(8.41) |
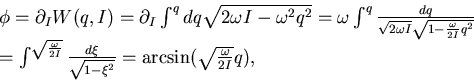 |
(8.42) |
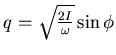 .
Sostituendo nell'hamiltoniana:
.
Sostituendo nell'hamiltoniana:
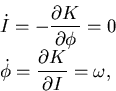 |
(8.43) |
Considera l'hamiltoniana:
![]()
a) Risolvi l'equazione di H.J. per separazione di varibili,
e riduci il moto alle quadrature,
cercando
![]() (
(
![]() saranno i nuovi impulsi)
saranno i nuovi impulsi)
b) Determina la regione dello spazio delle fasi un cui il moto si può descrivere in variabili azione-angolo.
c) In questa regione trova le frequenze dei moti quasi periodici.
Soluzione
a) Cerca:
![]() (
(
![]() saranno i nuovi impulsi).
L'equazione da risolvere è:
saranno i nuovi impulsi).
L'equazione da risolvere è:
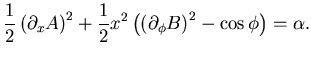 |
(8.44) |
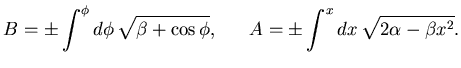 |
(8.45) |
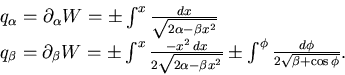 |
(8.46) |
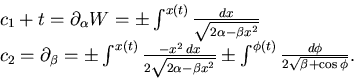 |
(8.47) |
b)
Hai due integrali primi
![]() . Questo ti permette di
capire come è fatto il moto (analisi qualitativa).
Procedi cosí. Controlla per prima cosa quali sono i valori possibili
per i due integrali primi:
. Questo ti permette di
capire come è fatto il moto (analisi qualitativa).
Procedi cosí. Controlla per prima cosa quali sono i valori possibili
per i due integrali primi:
![]() , dunque
, dunque
![]() . La proiezione dell'orbita
sul piano coordinato
. La proiezione dell'orbita
sul piano coordinato
![]() , è costituita dai punti
, è costituita dai punti
![]() per
per ![]() ;
da due curve chiuse per
;
da due curve chiuse per
![]() ; due separatrici (omocline per la
periodicità di
; due separatrici (omocline per la
periodicità di ![]() ) ed un punto fisso
per
) ed un punto fisso
per ![]() ; due curve periodiche per
; due curve periodiche per ![]() .
.
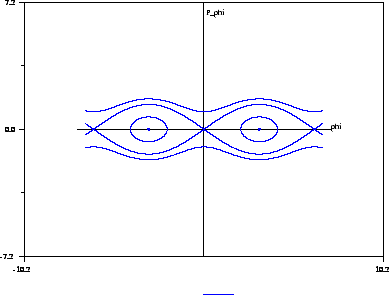
La proiezione dell'orbita sul piano ![]() è fatta cosí:
se
è fatta cosí:
se ![]() deve essere
deve essere
![]() , quindi
la proiezione è una curva chiusa simmetrica rispetto agli assi,
che interseca l'asse delle
, quindi
la proiezione è una curva chiusa simmetrica rispetto agli assi,
che interseca l'asse delle ![]() nei punti
nei punti
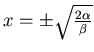 ;
se
;
se ![]() , e
, e ![]() , la proiezione consiste in due curve aperte che
intersecano l'asse delle
, la proiezione consiste in due curve aperte che
intersecano l'asse delle ![]() in
in
![]() ; se
; se
![]() due curve aperte che intersecano l'asse delle
due curve aperte che intersecano l'asse delle ![]() in
in
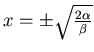 .
.
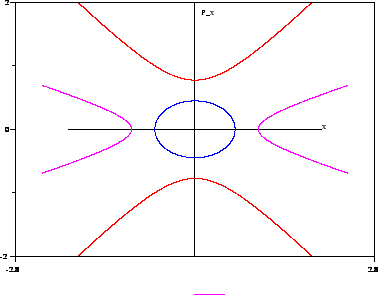
Dunque, se ![]() e
e ![]() , l'orbita vive sul prodotto diretto
delle due curve chiuse proiezioni sui due piani coordinati;
chiama
, l'orbita vive sul prodotto diretto
delle due curve chiuse proiezioni sui due piani coordinati;
chiama
![]() queste due curve
rispettivamente. L'orbita vive dunque
su una varietà in
queste due curve
rispettivamente. L'orbita vive dunque
su una varietà in
![]() diffeomorfa ad un toro bidimensionale.
In questo caso ha senso tentare di scrivere le variabili azione-angolo,
cioé di tentare di descrivere il moto attraverso delle variabili angolari
che esprimano la rotazione sul toro. Ci riesci scegliendo come
nuovi impulsi non
diffeomorfa ad un toro bidimensionale.
In questo caso ha senso tentare di scrivere le variabili azione-angolo,
cioé di tentare di descrivere il moto attraverso delle variabili angolari
che esprimano la rotazione sul toro. Ci riesci scegliendo come
nuovi impulsi non
![]() , ma delle loro opportune funzioni (variabili
d'azione) che determini nel modo seguente: saranno gli integrali
della forma
, ma delle loro opportune funzioni (variabili
d'azione) che determini nel modo seguente: saranno gli integrali
della forma ![]() , divisi per
, divisi per
![]() , sulle curve che hai ottenuto proiettando il moto sui piani coordinati;
tali integrali dipendono evidentemente da
, sulle curve che hai ottenuto proiettando il moto sui piani coordinati;
tali integrali dipendono evidentemente da
![]() :
:
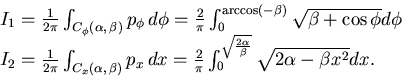 |
(8.48) |
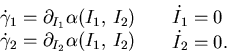 |
(8.49) |
c)
Le frequenze
![]() sono costanti,
in quanto dipendono
da
sono costanti,
in quanto dipendono
da
![]() che sono delle costanti del moto; essendo
che sono delle costanti del moto; essendo ![]() degli angoli,
in effetti
degli angoli,
in effetti ![]() sono le frequenze delle rotazioni. Il moto nelle singole
variabili angolari è dunque una rotazione con velocità angolare costante;
globalmente è un moto quasi-periodico su un toro.
sono le frequenze delle rotazioni. Il moto nelle singole
variabili angolari è dunque una rotazione con velocità angolare costante;
globalmente è un moto quasi-periodico su un toro.
Come calcoli le frequenze ![]() ? Devi calcolare le derivate di
? Devi calcolare le derivate di ![]() rispetto alle variabili d'azione, peró hai a disposizione solo
l'espressione delle variabili d'azione in funzione di
rispetto alle variabili d'azione, peró hai a disposizione solo
l'espressione delle variabili d'azione in funzione di
![]() .
Dunque procedi cosí:
.
Dunque procedi cosí:
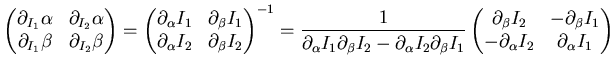 |
(8.50) |
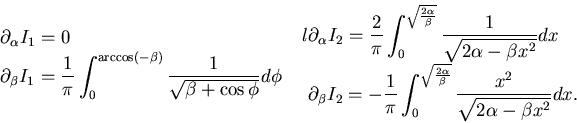 |
(8.51) |
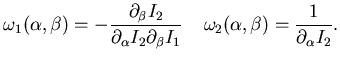 |
(8.52) |
Considera l'Hamiltoniana:
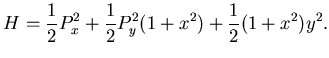 |
(8.53) |
a) Risolvi, per
separazione di variabili, l'equazione di Hamilton Jacobi per ![]() .
.
b) Determina la regione dello spazio delle fasi in cui il moto può essere descritto in variabili azione-angolo.
c) Calcola esplicitamente l'espressione dell'Hamiltoniana in termini delle variabili d'azione, e le frequenze dei moti multiperiodici.
d) Considera il moto di dato iniziale
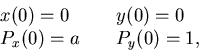 |
(8.54) |
e) Trova il periodo del moto per ![]() .
.
f) Discuti la stabilità della soluzione stazionaria
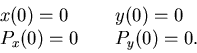 |
(8.55) |
Soluzione
a) Cerca una soluzione dell'equazione caratteristica di Hamilton-Jacobi del tipo:
| (8.56) |
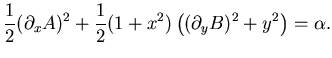 |
(8.57) |
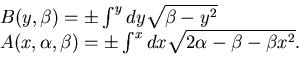 |
(8.58) |
b) La regione dello spazio delle fasi in cui il moto
é multiperiodico è data da ![]() ,
,
![]() .
.
c) Devi calcolare:
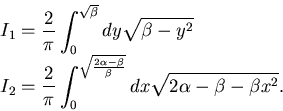 |
(8.59) |
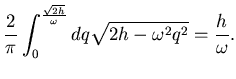 |
(8.60) |
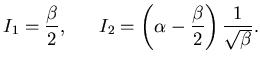 |
(8.61) |
| (8.62) |
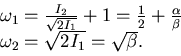 |
(8.63) |
d) Sostituendo il valore del dato iniziale in ![]() ,
, ![]() ottieni:
ottieni:
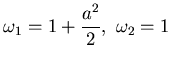 |
(8.64) |
e) per ![]() ,
,
![]() , dunque
, dunque
![]() .
.
![]() , dunque
, dunque ![]() .
.
f) Le equazioni di Hamilton sono
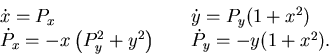 |
(8.65) |
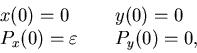 |
(8.66) |
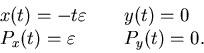 |
(8.67) |