


Next: 8.5 Costruzione delle variabili
Up: 8 Bignamino di Formalismo
Previous: 8.3 Funzioni generatrici e
Indice
Subsections
Come si è visto una trasformazione canonica
può rendere banalmente integrabile le equazioni di Hamilton.
Peró, chi ti dice come trovare la trasformazione?
Tentiamo allora di cercare una funzione generatrice 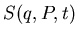 tale che la nuova hamiltoniana
tale che la nuova hamiltoniana 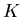 sia esattamente 0.
In tal caso, infatti, le equazioni nelle nuove varibili
sia esattamente 0.
In tal caso, infatti, le equazioni nelle nuove varibili 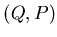 sono banali:
sono banali:
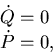 |
(8.32) |
dunque nota la trasfomazione si può risalire al moto nelle
variabili 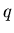 ,
, 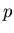 .
Come deve essere fatta una tale
.
Come deve essere fatta una tale 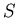 ?
Deve valere:
?
Deve valere:
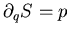 e
e 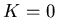 , cioè:
, cioè:
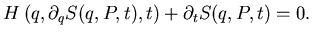 |
(8.33) |
Per Hamiltoniane indipendenti dal tempo, si può cercare una soluzione
del tipo
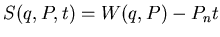 , dove
, dove 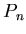 è l'ultimo impulso:
l'equazione di H.J. diventa (equazione caratteristica di H.J.):
è l'ultimo impulso:
l'equazione di H.J. diventa (equazione caratteristica di H.J.):
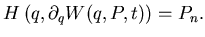 |
(8.34) |
In realtà, invece di cercare 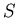 dipendente dal tempo che renda
nulla l'Hamiltoniana, puoi pensare che basta trovare
dipendente dal tempo che renda
nulla l'Hamiltoniana, puoi pensare che basta trovare 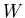 che rende
costante l'Hamiltoniana.
Infatti
puoi pensare che la funzione generatrice
che rende
costante l'Hamiltoniana.
Infatti
puoi pensare che la funzione generatrice
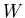 rende l'hamiltoniana uguale ad uno dei nuovi impulsi; anche cosí
le equazioni di Hamilton sono banali:
rende l'hamiltoniana uguale ad uno dei nuovi impulsi; anche cosí
le equazioni di Hamilton sono banali:
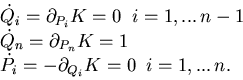 |
(8.35) |
Come si procede in pratica? Sempre e solo per separazione di variabili;
in alcuni rari casi ci si riesce (sistemi integrabili) in generale no.
Separazione di variabili significa che cerchi la soluzione come somma
di 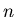 funzioni
ognuna delle quali dipende solo da una delle vecchie coordinate.
Il fatto che si riesca a trovare la soluzione dipende dal fatto che dentro
funzioni
ognuna delle quali dipende solo da una delle vecchie coordinate.
Il fatto che si riesca a trovare la soluzione dipende dal fatto che dentro
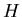 la dipendenza delle variabili è separtata.
la dipendenza delle variabili è separtata.
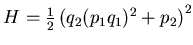 .
Cerco la funzione
.
Cerco la funzione
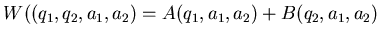 . I parametri
. I parametri
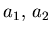 saranno i nuovi
impulsi. La separazione di variabili in questo caso consiste nel cercare
la funzione
saranno i nuovi
impulsi. La separazione di variabili in questo caso consiste nel cercare
la funzione  come la somma di una funzione che dipende solo da
come la somma di una funzione che dipende solo da 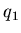 e
di una funzione che dipende solo da
e
di una funzione che dipende solo da 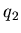 .
.
L'equazione da risolvere è:
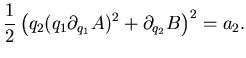 |
(8.36) |
Stai cercando 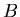 in modo che non dipenda da
in modo che non dipenda da 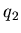 , ma solo da
, ma solo da 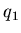 .
Dall'equazione puoi ricavare:
.
Dall'equazione puoi ricavare:
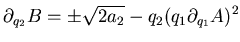 |
(8.37) |
peró in questa espressione
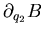 dipendende da
dipendende da 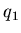 e da
e da 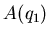 ;
l'unica possibilità che ho è dunque che la combinazione
;
l'unica possibilità che ho è dunque che la combinazione
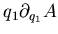 non dipenda da
non dipenda da 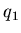 , cioè:
, cioè:
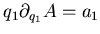 , ovvero
, ovvero
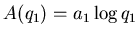 .
A questo punto posso risolvere anche l'equazione in
.
A questo punto posso risolvere anche l'equazione in 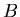 infatti
infatti
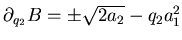 è una funzione
della sola
è una funzione
della sola 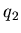 e dei nuovi impulsi.
Riassumendo, ottieni:
e dei nuovi impulsi.
Riassumendo, ottieni:
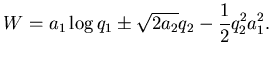 |
(8.38) |
La trasformazione generata da 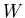 è:
è:
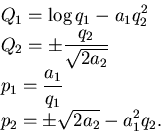 |
(8.39) |
Usando la soluzione delle equazioni del moto per l'hamiltoniana 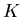 e tornando
indietro con la trasformazione, ottieni:
e tornando
indietro con la trasformazione, ottieni:
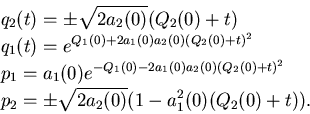 |
(8.40) |
Il segno 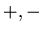 lo determini a seconda del segno di
lo determini a seconda del segno di
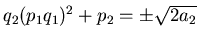 .
Nella soluzione compaiono i termini
.
Nella soluzione compaiono i termini
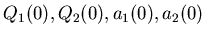 , che trovi
imponendo i dati iniziali.
, che trovi
imponendo i dati iniziali.
OSSERVAZIONE 1.
La separazione di variabili funziona perché
la dipendenza da 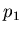 ,
, 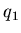 dell'hamiltoniana è isolata nel termine
dell'hamiltoniana è isolata nel termine
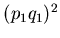 , cioè abbiamo potuto risolvere
separatamente l'equazione per
, cioè abbiamo potuto risolvere
separatamente l'equazione per 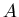 nella variabile
nella variabile 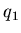 senza
coinvolgere l'altra variabile.
senza
coinvolgere l'altra variabile.
OSSERVAZIONE 2.
In effetti, ci sei riuscito perché oltre all'energia c'è un altro
integrale primo, esattamente 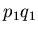 , infatti
, infatti 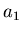 si conserva.
L'esistenza di questo integrale primo ti ha permesso di portare
il moto alle quadrature, così
come accade nei problemi lagrangiani.
In generale, peró, il tipico integrale primo che ti capita di trovare
risolvendo l'equazione di H.J. non è un momento
che proviene da una simmetria della
lagrangiana.
Considera ad esempio le Hamiltoniane:
si conserva.
L'esistenza di questo integrale primo ti ha permesso di portare
il moto alle quadrature, così
come accade nei problemi lagrangiani.
In generale, peró, il tipico integrale primo che ti capita di trovare
risolvendo l'equazione di H.J. non è un momento
che proviene da una simmetria della
lagrangiana.
Considera ad esempio le Hamiltoniane:
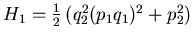 e
e
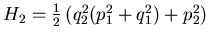 .
Per
.
Per 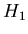 si conserva
si conserva 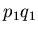 e la lagrangiana è
e la lagrangiana è
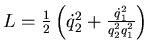 , che
ha il gruppo ad un parametro di simmetrie
, che
ha il gruppo ad un parametro di simmetrie
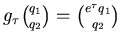 .
Per
.
Per 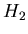 si conserva
si conserva
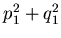 , la lagrangiana è
, la lagrangiana è
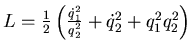 che non ha evidenti simmetrie.
che non ha evidenti simmetrie.
OSSERVAZIONE 3.
I nuovi impulsi li scegli tu, mentre risolvi l'equazione di H.J..
Infatti potevi, ad esempio, decidere che
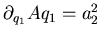 , oppure
, oppure 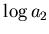 , o
, o
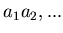 , o potevi
decidere che
, o potevi
decidere che 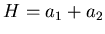 . Avresti ottenuto una soluzione di H.J. con una
diversa dipendenza dai nuovi impulsi, che comunque risolveva il problema.
In sostanza, scegli come impulsi una qualche combinazione delle costanti
da cui la soluzione di H.J. dipende. Inoltre la soluzione di H.J.
deve dipendere da un numero di costanti pari ai gradi di libertà
in modo non triviale (c'è comunque una costante additiva che si può
aggiungere a
. Avresti ottenuto una soluzione di H.J. con una
diversa dipendenza dai nuovi impulsi, che comunque risolveva il problema.
In sostanza, scegli come impulsi una qualche combinazione delle costanti
da cui la soluzione di H.J. dipende. Inoltre la soluzione di H.J.
deve dipendere da un numero di costanti pari ai gradi di libertà
in modo non triviale (c'è comunque una costante additiva che si può
aggiungere a 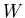 ).
).



Next: 8.5 Costruzione delle variabili
Up: 8 Bignamino di Formalismo
Previous: 8.3 Funzioni generatrici e
Indice
root
2001-04-02
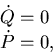
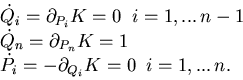
![]() funzioni
ognuna delle quali dipende solo da una delle vecchie coordinate.
Il fatto che si riesca a trovare la soluzione dipende dal fatto che dentro
funzioni
ognuna delle quali dipende solo da una delle vecchie coordinate.
Il fatto che si riesca a trovare la soluzione dipende dal fatto che dentro
![]() la dipendenza delle variabili è separtata.
la dipendenza delle variabili è separtata.
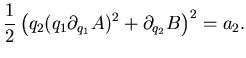
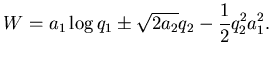
![]() ,
, ![]() dell'hamiltoniana è isolata nel termine
dell'hamiltoniana è isolata nel termine
![]() , cioè abbiamo potuto risolvere
separatamente l'equazione per
, cioè abbiamo potuto risolvere
separatamente l'equazione per ![]() nella variabile
nella variabile ![]() senza
coinvolgere l'altra variabile.
senza
coinvolgere l'altra variabile.
![]() , infatti
, infatti ![]() si conserva.
L'esistenza di questo integrale primo ti ha permesso di portare
il moto alle quadrature, così
come accade nei problemi lagrangiani.
In generale, peró, il tipico integrale primo che ti capita di trovare
risolvendo l'equazione di H.J. non è un momento
che proviene da una simmetria della
lagrangiana.
Considera ad esempio le Hamiltoniane:
si conserva.
L'esistenza di questo integrale primo ti ha permesso di portare
il moto alle quadrature, così
come accade nei problemi lagrangiani.
In generale, peró, il tipico integrale primo che ti capita di trovare
risolvendo l'equazione di H.J. non è un momento
che proviene da una simmetria della
lagrangiana.
Considera ad esempio le Hamiltoniane:
![]() e
e
![]() .
Per
.
Per ![]() si conserva
si conserva ![]() e la lagrangiana è
e la lagrangiana è
 , che
ha il gruppo ad un parametro di simmetrie
, che
ha il gruppo ad un parametro di simmetrie
![]() .
Per
.
Per ![]() si conserva
si conserva
![]() , la lagrangiana è
, la lagrangiana è
 che non ha evidenti simmetrie.
che non ha evidenti simmetrie.
![]() , oppure
, oppure ![]() , o
, o
![]() , o potevi
decidere che
, o potevi
decidere che ![]() . Avresti ottenuto una soluzione di H.J. con una
diversa dipendenza dai nuovi impulsi, che comunque risolveva il problema.
In sostanza, scegli come impulsi una qualche combinazione delle costanti
da cui la soluzione di H.J. dipende. Inoltre la soluzione di H.J.
deve dipendere da un numero di costanti pari ai gradi di libertà
in modo non triviale (c'è comunque una costante additiva che si può
aggiungere a
. Avresti ottenuto una soluzione di H.J. con una
diversa dipendenza dai nuovi impulsi, che comunque risolveva il problema.
In sostanza, scegli come impulsi una qualche combinazione delle costanti
da cui la soluzione di H.J. dipende. Inoltre la soluzione di H.J.
deve dipendere da un numero di costanti pari ai gradi di libertà
in modo non triviale (c'è comunque una costante additiva che si può
aggiungere a ![]() ).
).