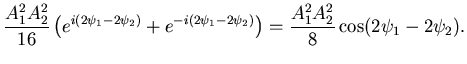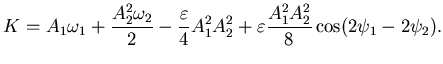


Next: 9 Altri Esercizi in
Up: 8 Bignamino di Formalismo
Previous: 8.5 Costruzione delle variabili
Indice
Subsections
Supponi di avere
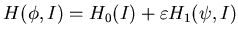 , dove le variabili
, dove le variabili
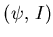 sono variabili azione-angolo per l'hamiltoniana
cosiddetta imperturbata
sono variabili azione-angolo per l'hamiltoniana
cosiddetta imperturbata 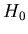 .
.
Stai cioè pensando di perturbare con
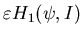 un'hamiltoniana integrabile
un'hamiltoniana integrabile 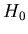 , pensando che
, pensando che
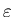 sia un parametro reale piccolo. Per l'hamiltoniana
sia un parametro reale piccolo. Per l'hamiltoniana 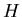 l variabili d'azione
non sono piú costanti del moto (infatti
l variabili d'azione
non sono piú costanti del moto (infatti 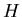 dipende anche dalle
dipende anche dalle 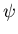 ),
e il nuovo sistema non sarà in generale integrabile; peró a
tempi fissati ti aspetti di compiere un errore di oridine
),
e il nuovo sistema non sarà in generale integrabile; peró a
tempi fissati ti aspetti di compiere un errore di oridine
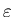 considerando
la soluzione della hamoltoniana imperturbata (scrivi le equazioni del moto:
troverai
considerando
la soluzione della hamoltoniana imperturbata (scrivi le equazioni del moto:
troverai
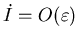 ). Un modo per migliorare questa approssimazione è
quello di cercare una trasformazione canonica che porti l'hamiltoniana data in una
in cui
all'ordine zero non ci sia dipendenza
dalle variabili angolari, e la dipendenza da
). Un modo per migliorare questa approssimazione è
quello di cercare una trasformazione canonica che porti l'hamiltoniana data in una
in cui
all'ordine zero non ci sia dipendenza
dalle variabili angolari, e la dipendenza da
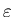 sia al secondo ordine,
cioè
sia al secondo ordine,
cioè
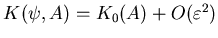 .
.
Come si fa?
Conviene cercare una funzione generatrice vicina alla funzione
generatrice dell'identità, infatti all'ordine 0 in
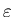 la trasformazione
che stiamo cercando non deve operare, perché l'hamiltoniana all'odine 0
è già in variabili azione-angolo, cioè integrabile.
Dunque cerchiamo
la trasformazione
che stiamo cercando non deve operare, perché l'hamiltoniana all'odine 0
è già in variabili azione-angolo, cioè integrabile.
Dunque cerchiamo
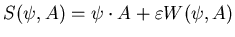 .
La trasfomazione indotta da
.
La trasfomazione indotta da 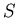 è data implicitamente da:
è data implicitamente da:
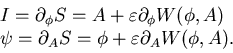 |
(8.68) |
Non è esplicita, peró
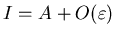 ,
,
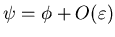 . Ma allora
possiamo esplicitarla in
. Ma allora
possiamo esplicitarla in
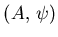 almeno fino all'ordine
almeno fino all'ordine
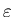 che è quello
che ci interessa:
che è quello
che ci interessa:
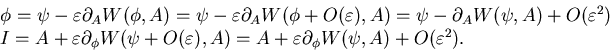 |
(8.69) |
La nuova Hamiltoniana sarà:
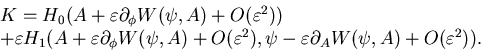 |
(8.70) |
Sviluppando fino all'ordine
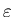 :
:
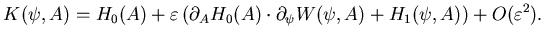 |
(8.71) |
Il problema è risolto se riusci a trovare 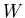 tale che l'ordine
tale che l'ordine
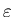 sia nullo,
cioè:
sia nullo,
cioè:
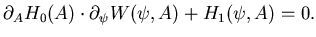 |
(8.72) |
Conviene lavorare in serie di Fourier, infatti le variabili 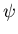 sono
variabili angolari. Ti ricordo che stiamo lavorando in dimensione maggiore
di uno, dunque nelle formule precedenti e seguenti, se
sono
variabili angolari. Ti ricordo che stiamo lavorando in dimensione maggiore
di uno, dunque nelle formule precedenti e seguenti, se 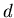 è la dimensione,
è la dimensione,
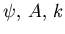 sono vettori di dimensione
sono vettori di dimensione 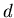 .
La serie di Fourier è definita da:
.
La serie di Fourier è definita da:
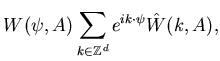 |
(8.73) |
dove
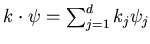 ,
e i coefficienti di Fourier sono dati da:
,
e i coefficienti di Fourier sono dati da:
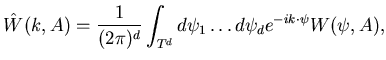 |
(8.74) |
dove 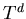 è il toro d-dimensionale su cui vivono le variabili
angolari
è il toro d-dimensionale su cui vivono le variabili
angolari
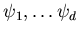 .
.
Per trovare 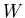 ti basta dunque trovarne i coefficienti di Fourier;
l'equazione
per i coefficienti è:
ti basta dunque trovarne i coefficienti di Fourier;
l'equazione
per i coefficienti è:
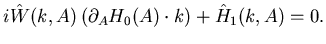 |
(8.75) |
Quando puoi risolvere questa equazione lineare per
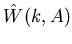 ?
Evidentemente ci riesci a meno che
?
Evidentemente ci riesci a meno che
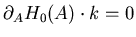 e
e
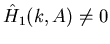 e riesci a risommare la serie che definisce
e riesci a risommare la serie che definisce
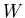 . Se
. Se 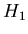 ha solo un numero finito di coefficienti di Fourier possono
accadere
sostanzialmente tre cose.
ha solo un numero finito di coefficienti di Fourier possono
accadere
sostanzialmente tre cose.
a) I valori di 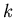 per cui
per cui
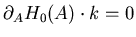 annullano anche
annullano anche
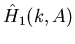 ;
dunque
;
dunque
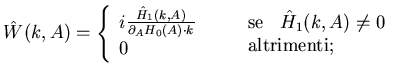 |
(8.76) |
quindi 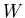 l'hai trovata e dunque
sei riuscito a portare la
perturbazione al secondo ordine; la nuova hamiltoniana
all'ordine 0 è
l'hai trovata e dunque
sei riuscito a portare la
perturbazione al secondo ordine; la nuova hamiltoniana
all'ordine 0 è
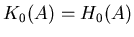 , (cioè
sono
uguali, ma la variabile
, (cioè
sono
uguali, ma la variabile 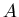 non è
non è
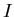 ...).
...).
b) Termine di media non nullo:
come sopra tranne che
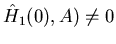 (qui
(qui 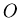 dentro
dentro 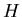 è il vettore nullo in
è il vettore nullo in
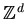 ; palesemente non puoi definire
; palesemente non puoi definire
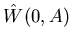 perché nell'equazione ha coefficiente 0 davanti;
peró
perché nell'equazione ha coefficiente 0 davanti;
peró
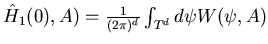 è il valor medio sul toro di
è il valor medio sul toro di 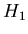 , dunque non
dipende dalle variabili angolari, puoi cioè incorporarlo dentro
, dunque non
dipende dalle variabili angolari, puoi cioè incorporarlo dentro 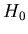 :
:
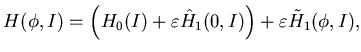 |
(8.77) |
dove
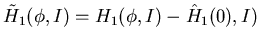 ha ora media nulla,
cioè
ha ora media nulla,
cioè
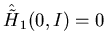 ; ti riduci cioè al caso precedente, peró
la nuova hamiltoniana all'ordine 0 nella nupva variabile
; ti riduci cioè al caso precedente, peró
la nuova hamiltoniana all'ordine 0 nella nupva variabile 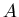 è
è
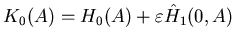 ;
;
c) risonanza: per qualche 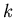 diverso del vettore nullo,
diverso del vettore nullo,
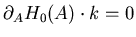 mentre
mentre
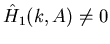 ; in tal caso non puoi rimuovere la
perturbazione di ordine
; in tal caso non puoi rimuovere la
perturbazione di ordine
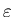 per quel particolare valore di
per quel particolare valore di 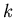 .
.
Considera l'hamiltoniana
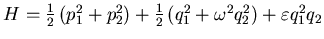 , con
, con
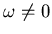 .
Per
.
Per
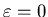 è intergabile, infatti è la
somma delle hamiltoniane di due oscillatori
armonici disaccoppiati:
è intergabile, infatti è la
somma delle hamiltoniane di due oscillatori
armonici disaccoppiati:
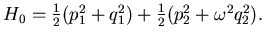 Passa dunque alle variabili azione-angolo separatamente nella coppia di
variabili coniugate. Ottieni
Passa dunque alle variabili azione-angolo separatamente nella coppia di
variabili coniugate. Ottieni
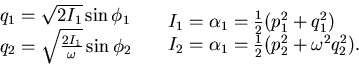 |
(8.78) |
In variabili azione angolo per l'hamiltoniana con
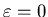 , tutta l'hamiltoniana assegnata, diventa:
, tutta l'hamiltoniana assegnata, diventa:
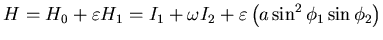 , dove
, dove
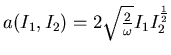 .
Tenta di rimuovere il primo ordine della perturbazione, cerca cioè una
funzione
.
Tenta di rimuovere il primo ordine della perturbazione, cerca cioè una
funzione
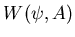 tale che valga in trasformata di Fourier:
tale che valga in trasformata di Fourier:
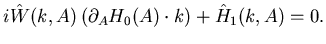 |
(8.79) |
Ti serve trovare la trasformata di 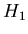 . La dipendenza angolare è
. La dipendenza angolare è
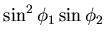 . Ora
. Ora
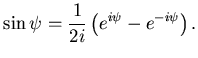 |
(8.80) |
Dunque, svolgendo il quadrato e i prodotti:
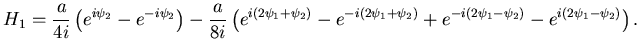 |
(8.81) |
Dunque i valori di 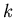 per cui la trasformata di Fourier di
per cui la trasformata di Fourier di 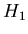 non è
nulla, sono
non è
nulla, sono
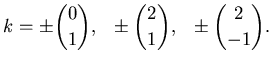 |
(8.82) |
Per controllare se ti trovi nel caso a) o nel caso c) (il caso b) è escluso
perché 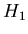 è a
media nulla, cioè la trasformata per
è a
media nulla, cioè la trasformata per 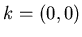 è zero),
devi determinare
è zero),
devi determinare
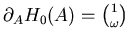 .
Controlla se
.
Controlla se
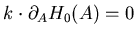 .
Vale
.
Vale
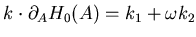 , ma allora
per poter rimuovere il primo ordine ti basta che
, ma allora
per poter rimuovere il primo ordine ti basta che
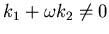 per i valori di
per i valori di 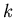 che hai determinato sopra. Sostituendo:
che hai determinato sopra. Sostituendo:
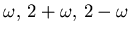 devono essere diversi da zero,
cioè
devono essere diversi da zero,
cioè
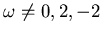 .
In tal caso puoi procedere e ottieni:
.
In tal caso puoi procedere e ottieni:
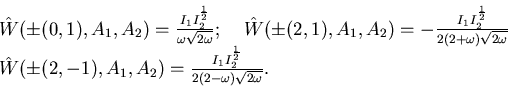 |
(8.83) |
Chi è la nuova hamiltoniana all'ordine 0?
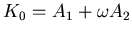 .
.
Esercizio 8.13
Considera
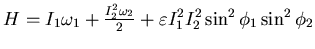
.
Rimuovi la perturbazioe al primo ordine.
Soluzione
Usando l'espressione esponenziale del seno, si ottiene:
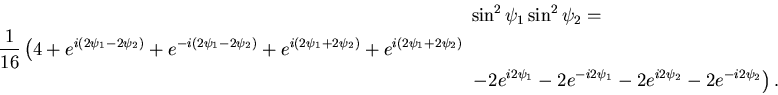 |
(8.84) |
Dunque:
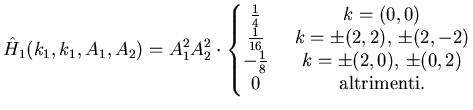 |
(8.85) |
La media è nulla, dunque devi portare il termine di media
in 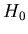 , cioè l'hamiltoniana imperturbata che devi considerare è
, cioè l'hamiltoniana imperturbata che devi considerare è
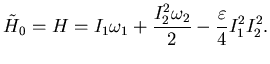 |
(8.86) |
Sotto quali condizioni riesci a rimuovere
la perturbazione al primo ordine?
Calcola le frequenze
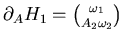 .
Allora deve essere:
.
Allora deve essere:
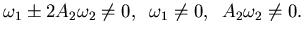 |
(8.87) |
In tal caso:
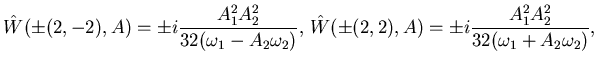 |
(8.88) |
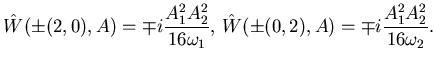 |
(8.89) |
La nuova hamiltonianana
all'ordine 0 (che in realtà dipende
da
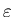 , ma non dalle variabili angolari)
è
, ma non dalle variabili angolari)
è
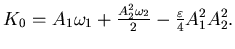
Che succede nelle risonanze, cioè, ad esempio, se ti interessa il moto
nella regione intorno a
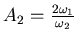 ?
Non puoi rimuovere tutto il primo ordine; in pratica sopravvive
un termine di ordine
?
Non puoi rimuovere tutto il primo ordine; in pratica sopravvive
un termine di ordine
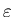 che dipende dalle
che dipende dalle 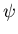 . Operando come sopra,
non puoi risolvere l'equazione per i coefficienti di
. Operando come sopra,
non puoi risolvere l'equazione per i coefficienti di 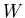 con
con
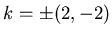 ; i corripondenti
termini di
; i corripondenti
termini di 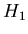 sopravvivono , e sono:
sopravvivono , e sono:
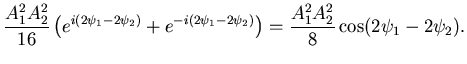 |
(8.90) |
L'hamiltoniana che ottieni è:
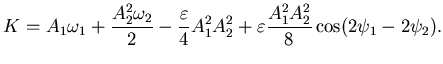 |
(8.91) |



Next: 9 Altri Esercizi in
Up: 8 Bignamino di Formalismo
Previous: 8.5 Costruzione delle variabili
Indice
root
2001-04-02
![]() un'hamiltoniana integrabile
un'hamiltoniana integrabile ![]() , pensando che
, pensando che
![]() sia un parametro reale piccolo. Per l'hamiltoniana
sia un parametro reale piccolo. Per l'hamiltoniana ![]() l variabili d'azione
non sono piú costanti del moto (infatti
l variabili d'azione
non sono piú costanti del moto (infatti ![]() dipende anche dalle
dipende anche dalle ![]() ),
e il nuovo sistema non sarà in generale integrabile; peró a
tempi fissati ti aspetti di compiere un errore di oridine
),
e il nuovo sistema non sarà in generale integrabile; peró a
tempi fissati ti aspetti di compiere un errore di oridine
![]() considerando
la soluzione della hamoltoniana imperturbata (scrivi le equazioni del moto:
troverai
considerando
la soluzione della hamoltoniana imperturbata (scrivi le equazioni del moto:
troverai
![]() ). Un modo per migliorare questa approssimazione è
quello di cercare una trasformazione canonica che porti l'hamiltoniana data in una
in cui
all'ordine zero non ci sia dipendenza
dalle variabili angolari, e la dipendenza da
). Un modo per migliorare questa approssimazione è
quello di cercare una trasformazione canonica che porti l'hamiltoniana data in una
in cui
all'ordine zero non ci sia dipendenza
dalle variabili angolari, e la dipendenza da
![]() sia al secondo ordine,
cioè
sia al secondo ordine,
cioè
![]() .
.
![]() la trasformazione
che stiamo cercando non deve operare, perché l'hamiltoniana all'odine 0
è già in variabili azione-angolo, cioè integrabile.
Dunque cerchiamo
la trasformazione
che stiamo cercando non deve operare, perché l'hamiltoniana all'odine 0
è già in variabili azione-angolo, cioè integrabile.
Dunque cerchiamo
![]() .
La trasfomazione indotta da
.
La trasfomazione indotta da ![]() è data implicitamente da:
è data implicitamente da:
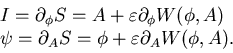
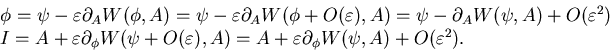
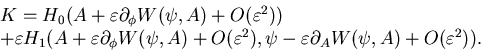
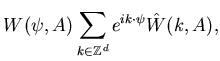
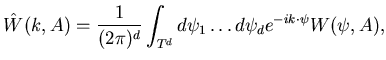
![]() ti basta dunque trovarne i coefficienti di Fourier;
l'equazione
per i coefficienti è:
ti basta dunque trovarne i coefficienti di Fourier;
l'equazione
per i coefficienti è:
![]() per cui
per cui
![]() annullano anche
annullano anche
![]() ;
dunque
;
dunque
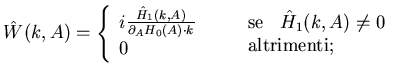
![]() (qui
(qui ![]() dentro
dentro ![]() è il vettore nullo in
è il vettore nullo in
![]() ; palesemente non puoi definire
; palesemente non puoi definire
![]() perché nell'equazione ha coefficiente 0 davanti;
peró
perché nell'equazione ha coefficiente 0 davanti;
peró
![]() è il valor medio sul toro di
è il valor medio sul toro di ![]() , dunque non
dipende dalle variabili angolari, puoi cioè incorporarlo dentro
, dunque non
dipende dalle variabili angolari, puoi cioè incorporarlo dentro ![]() :
:
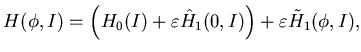
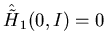 ; ti riduci cioè al caso precedente, peró
la nuova hamiltoniana all'ordine 0 nella nupva variabile
; ti riduci cioè al caso precedente, peró
la nuova hamiltoniana all'ordine 0 nella nupva variabile ![]() diverso del vettore nullo,
diverso del vettore nullo,
![]() mentre
mentre
![]() ; in tal caso non puoi rimuovere la
perturbazione di ordine
; in tal caso non puoi rimuovere la
perturbazione di ordine
![]() per quel particolare valore di
per quel particolare valore di ![]() .
.
![]() , con
, con
![]() .
Per
.
Per
![]() è intergabile, infatti è la
somma delle hamiltoniane di due oscillatori
armonici disaccoppiati:
è intergabile, infatti è la
somma delle hamiltoniane di due oscillatori
armonici disaccoppiati:
![]() Passa dunque alle variabili azione-angolo separatamente nella coppia di
variabili coniugate. Ottieni
Passa dunque alle variabili azione-angolo separatamente nella coppia di
variabili coniugate. Ottieni
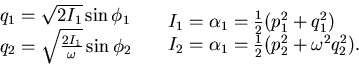
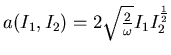 .
Tenta di rimuovere il primo ordine della perturbazione, cerca cioè una
funzione
.
Tenta di rimuovere il primo ordine della perturbazione, cerca cioè una
funzione
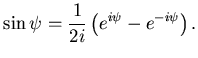
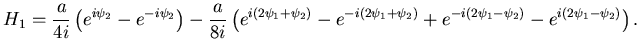
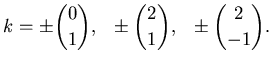
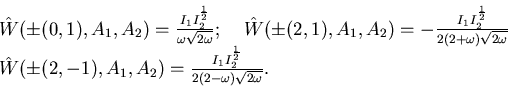
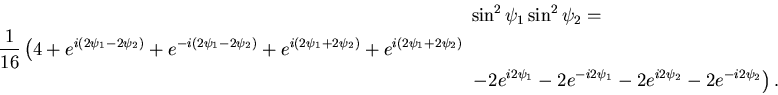
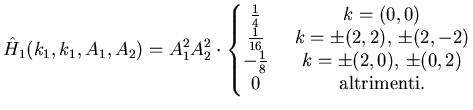
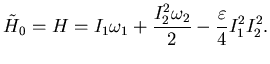
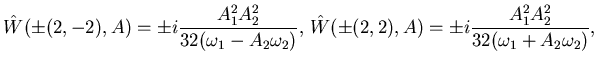
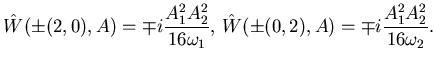
![]() ?
Non puoi rimuovere tutto il primo ordine; in pratica sopravvive
un termine di ordine
?
Non puoi rimuovere tutto il primo ordine; in pratica sopravvive
un termine di ordine
![]() che dipende dalle
che dipende dalle ![]() . Operando come sopra,
non puoi risolvere l'equazione per i coefficienti di
. Operando come sopra,
non puoi risolvere l'equazione per i coefficienti di ![]() con
con
![]() ; i corripondenti
termini di
; i corripondenti
termini di ![]() sopravvivono , e sono:
sopravvivono , e sono: