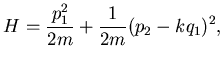Next: 8.4 Equazione di Hamilton
Up: 8 Bignamino di Formalismo
Previous: 8.2 Trasformazioni simplettiche indipendenti
Indice
Subsections
La condizione di simpletticità 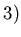 ,
può essere riformulata nel modo seguente:
,
può essere riformulata nel modo seguente:
esiste 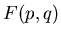 tale che
tale che
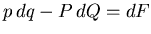 .
.
Un modo di usare questo fatto è pensare che la trasformazione
assegnata permetta di
considerare le 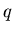 e le
e le 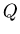 come variabili indipendenti.
In tal caso anche nelle variabili
come variabili indipendenti.
In tal caso anche nelle variabili 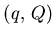 deve valere
deve valere
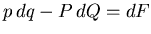 , dove al posto di
, dove al posto di 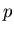 e
e 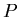 avremo scritto
la loro espressione in termini di
avremo scritto
la loro espressione in termini di 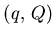 .
Ma allora la trasformazione deve verificare: esiste
.
Ma allora la trasformazione deve verificare: esiste
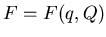 tale che:
tale che:
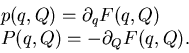 |
(8.22) |
L'utilità di questo ragionamento è che per avere
una trasformazione canonica è sufficiente dare una funzione
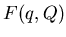 , di definire le funzioni
, di definire le funzioni 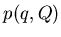 e
e
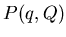 attraverso le definizioni 8.22 e poi invertire la
prima rispetto a
attraverso le definizioni 8.22 e poi invertire la
prima rispetto a 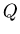 , in modo da ottenere
, in modo da ottenere 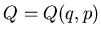 e
e 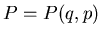 .
Ovviamente per fare ciò deve valere almeno la condizione di
invertibilità locale
.
Ovviamente per fare ciò deve valere almeno la condizione di
invertibilità locale
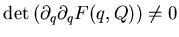 .
.
Esercizio 8.6
Trovare i valori dei
parametri per cui la trasformazione seguente è canonica,
costruendo la funzione generatrice di tipo
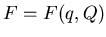
:
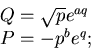 |
(8.23) |
La condizione di canonicità espressa tramite la funzione
generatrice è particolarmente utile nel caso di
trasformazioni dipendenti dal tempo.
Infatti, una trasformazione
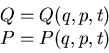 |
(8.24) |
è canonica se è simplettica per ogni 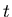 .
Questo è equivalente al fatto che, detta
.
Questo è equivalente al fatto che, detta 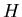 la vecchia hamiltoniana
(anche dipendente dal tempo)
e detta
la vecchia hamiltoniana
(anche dipendente dal tempo)
e detta 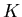 la nuova, esista una funzione
la nuova, esista una funzione 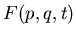 tale che:
tale che:
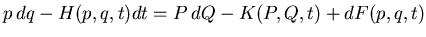 .
.
Anche in questo caso, se si possono considerare
le 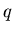 e le
e le 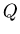 come variabili indipendenti si ottiene
come variabili indipendenti si ottiene
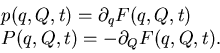 |
(8.25) |
E non solo, ottenuta la trasformazione,
si ottiene anche la nuova hamiltoniana:
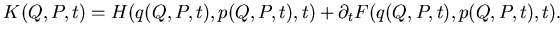 |
(8.26) |
Esercizio 8.7
Risolvere le equazioni di Hamilton per l'hamiltoniana
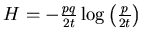
, utilizzando la
trasformazione canonica generata da
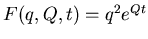
.
può essere conveniente pensare l'espressione
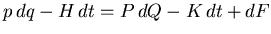 |
(8.27) |
in termini di altre coppie di variabili. Considera ad esempio
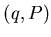 : è utile scivere
: è utile scivere
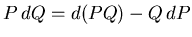 e definire
e definire
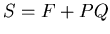 ; ottieni:
; ottieni:
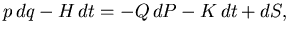 |
(8.28) |
dove
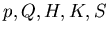 le stai pensando come funzioni di
le stai pensando come funzioni di 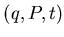 .
In tal caso la condizione di canonicità (e quindi
la trasformazione in forma implicita, assegnata la funzione
.
In tal caso la condizione di canonicità (e quindi
la trasformazione in forma implicita, assegnata la funzione
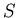 ) diventa:
) diventa:
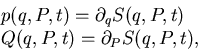 |
(8.29) |
e la relazione tra le hamiltoniane e 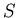 :
:
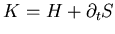 .
.
Esercizio 8.8
(teorico)
Trovare
tutte le relazioni che definiscono una trasfomazione
canonica, assegnata una funzione di qualunque combinazione delle
variabili; quante sono per un sistema a
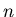
gradi di libertà?
Ad esmpio, usa come variabili indipendenti
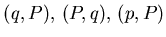
, e, a due gradi di libertà
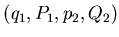
.
Esercizio 8.9
(teorico)
Data
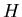
e la trasformazione delle sole coordinate
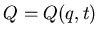
,
puoi ottenere una
trasformazione canonica nel seguente modo:
scrivi la lagrangiana in
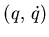
, cambia il sistema di
coordinate e scrivi la nuova hamiltoniana;
hai dunque trovato una legge di trasformazione degli impulsi.
Prova che la trasformazione che hai ottenuto
è generata da
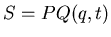
.
Esercizio 8.10
Determinare una trasformazione canonica tra quelle generate da
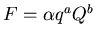
, che trasformi l'hamiltoniana
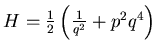
nell'hamiltoniana
di un oscillatore armonico.
Esercizio 8.11
Studiare il moto del sistema di Hamiltoniana
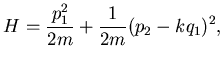 |
(8.30) |
mediante la trasformazione canonica generata da
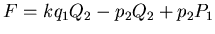
.
Esercizio 8.12
Determinare il moto del sistema di
Lagrangiana
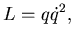 |
(8.31) |
passando all'hamiltoniana e utilizzando la trasformazione canonica
generata da
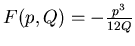
.




Next: 8.4 Equazione di Hamilton
Up: 8 Bignamino di Formalismo
Previous: 8.2 Trasformazioni simplettiche indipendenti
Indice
root
2001-04-02
tale che
.
![]() e le
e le ![]() come variabili indipendenti.
In tal caso anche nelle variabili
come variabili indipendenti.
In tal caso anche nelle variabili ![]() deve valere
deve valere
![]() , dove al posto di
, dove al posto di ![]() e
e ![]() avremo scritto
la loro espressione in termini di
avremo scritto
la loro espressione in termini di ![]() .
Ma allora la trasformazione deve verificare: esiste
.
Ma allora la trasformazione deve verificare: esiste
![]() tale che:
tale che:
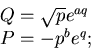
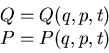
.
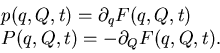
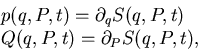
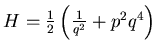 nell'hamiltoniana
di un oscillatore armonico.
nell'hamiltoniana
di un oscillatore armonico.