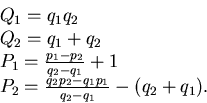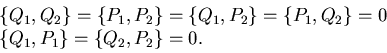Next: 8.3 Funzioni generatrici e
Up: 8 Bignamino di Formalismo
Previous: 8.1 Le trasformazioni canoniche
Indice
Condizioni equivalenti di simpletticità sono:
- 1)
- lo jacobiano è una matrice simplettica;
- 2)
-
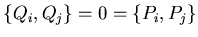 ,
,
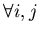 ,
,
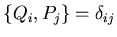 (le parentesi di Poisson
sono definite da
(le parentesi di Poisson
sono definite da
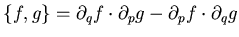 ,
e sono un prodotto antisimmetrico per le funzioni regolari di
,
e sono un prodotto antisimmetrico per le funzioni regolari di
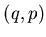 );
);
- 3)
- la forma differenziale
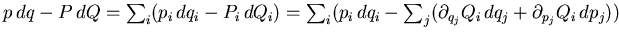 è chiusa (localmente esatta).
è chiusa (localmente esatta).
- 4)
- ne esistono altre ( vedi ``parentesi di lagrange'' sui testi
di meccanica analitica).
Esercizio 8.2
(teorico) Verifica che le condizioni
1,2,3 sono equivalenti e che implicano la
canonicità della trasformazione.
Esercizio 8.3
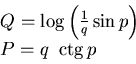 |
(8.10) |
Dove è definita? Qual è l'inversa? È canonica?
Soluzione
Perché la traformazione abbia senso deve essere
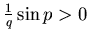 , dunque
, dunque 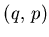 devono essere
nelle regioni
devono essere
nelle regioni 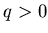 e
e
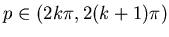 , con
, con
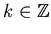 ,
o nelle regioni
,
o nelle regioni
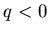 e
e
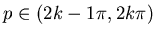 , con
, con
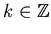 .
In entrambi i casio anche la seconda equazione ha senso, infatti essa
ha singolarità solo per
.
In entrambi i casio anche la seconda equazione ha senso, infatti essa
ha singolarità solo per
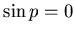 .
Quindi la trasformazione è definita nelle regioni descritte sopra.
.
Quindi la trasformazione è definita nelle regioni descritte sopra.
Per calcolare l'inversa bisogna esprimere 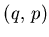 in funzione di
in funzione di
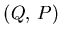 . Comincio con l'invertire il logaritmo:
. Comincio con l'invertire il logaritmo:
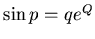 . Dalla seconda
. Dalla seconda
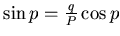 .
Ma allora
.
Ma allora
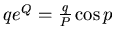 . Dunque
. Dunque
Inserendo questa relazione nella prima equazione ottengo
I segni si determinano a seconda della regione in cui
si inverte la trasformazione.
Per verificare la canonicità è sufficiente calcolare
verificare se
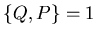 .
Calcolo quindi lo Jacobiano della trasformazione.
.
Calcolo quindi lo Jacobiano della trasformazione.
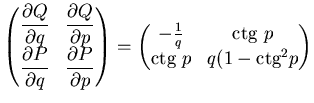 |
(8.11) |
Ma allora
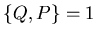 .
.
Esercizio 8.4
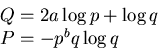 |
(8.12) |
Trovare per quali valori di
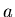
e
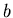
è canonica.
Considera l'hamiltoniana
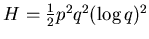
, e il
dato iniziale
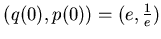
.
Trova la soluzione delle equazioni del moto utilizzando la trasformazione
canonica trovata.
Soluzione
Calcolo lo Jacobiano
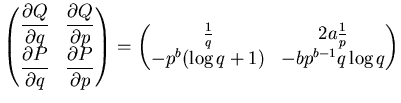 |
(8.13) |
Impongo
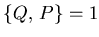 :
cioè:
Se deve fare
:
cioè:
Se deve fare 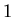 , in particolare non deve dipendere da
, in particolare non deve dipendere da 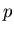 .
Dunque
.
Dunque 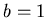 . Ottengo
Ma non deve dipendere nemmeno da
. Ottengo
Ma non deve dipendere nemmeno da 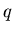 , dunque
, dunque 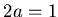 .
Quindi per
.
Quindi per 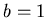 e
e
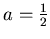 la trasformazione è canonica.
la trasformazione è canonica.
La trasformazione cercata è
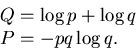 |
(8.14) |
La nuova Hamiltoniana è
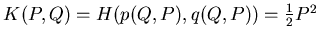 .
Ma allora le equazioni del moto sono
.
Ma allora le equazioni del moto sono
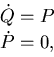 |
(8.15) |
che hanno soluzioni
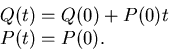 |
(8.16) |
Impongo il dato iniziale
e ottengo 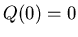 e
e 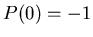 .
Quindi:
.
Quindi:
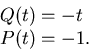 |
(8.17) |
Ma allora posso cercare di esprimere la soluzione nelle vecchie
variabili attraverso la trasformazione inversa.
Dopo un pò di algebra si ottiene
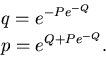 |
(8.18) |
Dunque
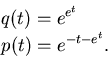 |
(8.19) |
Come visto negli esercizi precedenti,
la simpletticità si controlla sia
calcolando l'esattezza della forma differenziale
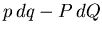 ,
sia calcolando le parentesi di Poisson. Nel caso di un sistema
ad un grado di libertà, questi conti sono particolarmente semplici.
Infatti, per
antisimmetria,
,
sia calcolando le parentesi di Poisson. Nel caso di un sistema
ad un grado di libertà, questi conti sono particolarmente semplici.
Infatti, per
antisimmetria,
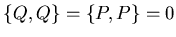 qualunque siano le funzioni
qualunque siano le funzioni 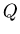 e
e 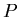 .
Dunque la condizione di simpletticità è semplicemente
.
Dunque la condizione di simpletticità è semplicemente
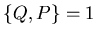 .
.
In più dimensioni il calcolo si complica.
Ad esempio considera l'esercizio
Esercizio 8.5
Verificare la canonicità di:
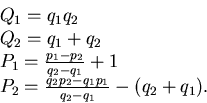 |
(8.20) |
In questo caso
le relazioni per le parentesi di Poisson da verificare sono:
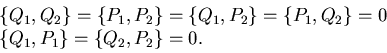 |
(8.21) |




Next: 8.3 Funzioni generatrici e
Up: 8 Bignamino di Formalismo
Previous: 8.1 Le trasformazioni canoniche
Indice
root
2001-04-02
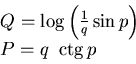
![]() , dunque
, dunque ![]() devono essere
nelle regioni
devono essere
nelle regioni ![]() e
e
![]() , con
, con
![]() ,
o nelle regioni
,
o nelle regioni
![]() e
e
![]() , con
, con
![]() .
In entrambi i casio anche la seconda equazione ha senso, infatti essa
ha singolarità solo per
.
In entrambi i casio anche la seconda equazione ha senso, infatti essa
ha singolarità solo per
![]() .
Quindi la trasformazione è definita nelle regioni descritte sopra.
.
Quindi la trasformazione è definita nelle regioni descritte sopra.
![]() in funzione di
in funzione di
![]() . Comincio con l'invertire il logaritmo:
. Comincio con l'invertire il logaritmo:
![]() . Dalla seconda
. Dalla seconda
![]() .
Ma allora
.
Ma allora
![]() . Dunque
. Dunque
![]() .
Calcolo quindi lo Jacobiano della trasformazione.
.
Calcolo quindi lo Jacobiano della trasformazione.
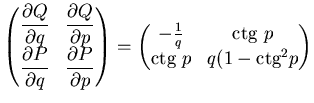
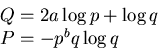
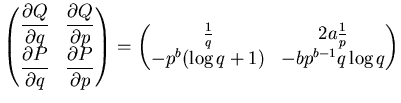
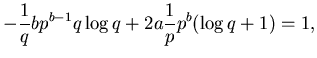
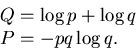
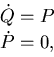
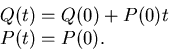
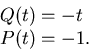
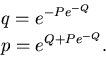
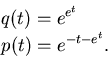
![]() ,
sia calcolando le parentesi di Poisson. Nel caso di un sistema
ad un grado di libertà, questi conti sono particolarmente semplici.
Infatti, per
antisimmetria,
,
sia calcolando le parentesi di Poisson. Nel caso di un sistema
ad un grado di libertà, questi conti sono particolarmente semplici.
Infatti, per
antisimmetria,
![]() qualunque siano le funzioni
qualunque siano le funzioni ![]() e
e ![]() .
Dunque la condizione di simpletticità è semplicemente
.
Dunque la condizione di simpletticità è semplicemente
![]() .
.