Next: 8.2 Trasformazioni simplettiche indipendenti
Up: 8 Bignamino di Formalismo
Previous: 8 Bignamino di Formalismo
Indice
Subsections
Considera un Hamiltoninana 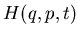 , e una trasformazione regolare
di coordinate
, e una trasformazione regolare
di coordinate
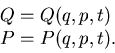 |
(8.1) |
Esiste
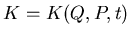 tale che
tale che
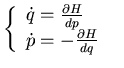 se e solo se se e solo se 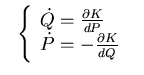 ? ? |
(8.2) |
In altre parole, il sistema di equazioni differenziali nelle variabili 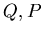 è hamiltoniano? E se lo è, qual è l'Hamiltoniana?
è hamiltoniano? E se lo è, qual è l'Hamiltoniana?
Risolvere questo problema è utile perché in alcuni casi il sistema
nelle nuove variabili è piú facilmente risolubile di quello nelle vecchie.
Sia
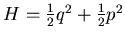 e sia data la trasformazione:
e sia data la trasformazione:
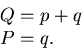 |
(8.3) |
La trasformazione inversa è
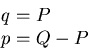 |
(8.4) |
Le equazioni del moto, nelle vecchie variabili sono:
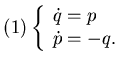 |
(8.5) |
Nelle nuove variabili le equazioni si
ottengono utilizzando le equazioni 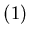 e
le trasformazioni di coordinate. Si ottiene:
e
le trasformazioni di coordinate. Si ottiene:
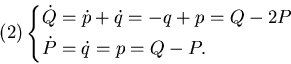 |
(8.6) |
Un sistema differenziale è
Hamiltoniano se esiste l'hamiltoniana, cioè se esiste una funzione 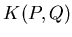 tale che
tale che
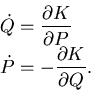 |
(8.7) |
Nel nostro caso,
questo accade se una delle seguenti condizioni equivalenti è soddisfatta:
- i)
- la forma differenziale
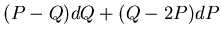 è chiusa
è chiusa
- ii)
-
div
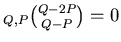
Ed in effetti
div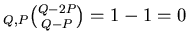 .
Per la determinare la Hamiltoniana
.
Per la determinare la Hamiltoniana 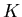 bisogna trovare la primitiva
della forma differenziale
bisogna trovare la primitiva
della forma differenziale
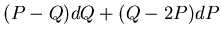 .
Integrando nella variabile
.
Integrando nella variabile 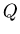 si ottiene:
si ottiene:
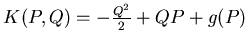 , dove
, dove 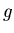 si determina imponendo
si determina imponendo
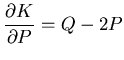 . Si ottiene
. Si ottiene
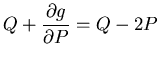 , quindi
, quindi 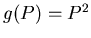 .
In definitiva
.
In definitiva
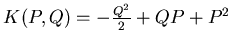 .
.
Sia
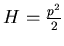 , e sia
, e sia
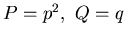 la trasformazione assegnata.
Nelle nuove variabili il sistema differenziale è
la trasformazione assegnata.
Nelle nuove variabili il sistema differenziale è
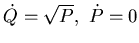 , che è hamiltonianio di halmiltoniana
, che è hamiltonianio di halmiltoniana
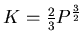 .
D'altra parte per l'hamiltoniana
.
D'altra parte per l'hamiltoniana
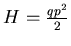 , il sistema
trasformato
, il sistema
trasformato
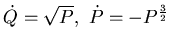 non
è hamiltoniano.
non
è hamiltoniano.
In questo esempio la trasformazione porta il sistema
di Hamiltoniana
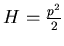 in un sistema hamiltoniano,
mentre porta il sistema di hamiltoniana
in un sistema hamiltoniano,
mentre porta il sistema di hamiltoniana
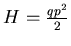 in un sistema
che non è hamiltoniano.
in un sistema
che non è hamiltoniano.
Il fatto importante è che esistono invece trasformazioni che portano
sistemi Hamiltoniani in sistemi Hamiltoniani
qualunque sia l'Hamiltoniana di partenza.
Nel seguito chiamerò trasformazioni canoniche tali trasformazioni.
Esercizio 8.1
(teorico)
Provare che ogni cambiamento lineare
invertibile per sistemi a un grado di libertà
di coordinate è canonico nel senso detto sopra.
Una classe di trasformazioni canoniche è quella dei
diffeomorfismi simplettici (nel seguito chiamate trasformazioni simplettiche):
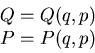 |
(8.8) |
è un diffeomorfismo simplettico
se lo jacobiano della
trasformazione è simplettico per ogni valore di 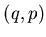 :
:
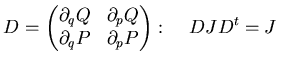 dove dove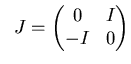 |
(8.9) |
(in dimensione 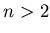 , la matrice
, la matrice 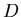 è una matrice
è una matrice
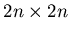 , dove ogni blocco è definito nel modo ovvio:
, dove ogni blocco è definito nel modo ovvio:
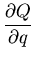 è la matrice delle derivate delle
è la matrice delle derivate delle 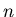 funzioni
funzioni 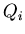 rispetto alle
rispetto alle 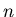 variabili
variabili 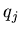 , cioè
, cioè
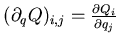 etc. .
Per queste trasformazioni, nel caso in
cui
etc. .
Per queste trasformazioni, nel caso in
cui 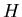 non dipenda dal tempo
la regola per trovare la nuova
Hamiltoniana è
non dipenda dal tempo
la regola per trovare la nuova
Hamiltoniana è
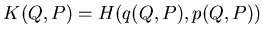 .
.
In sintesi esistono
- a)
- trasformazioni che trasformano un sistema hamiltoniano di
hamiltoniana
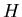 assegnata
in un altro sistema hamiltoniano
assegnata
in un altro sistema hamiltoniano
- b)
- trasformazioni canoniche che trasformano
un sistema hamiltoniano in un sistema hamiltoniano qualunque sia
l'hamiltoniana
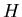
- c)
- trasformazioni simplettiche, cioè quelle
che verificano l'identità (8.9). In particolare
queste trasformazioni sono canoniche.
La nuova Hamiltoniana si ottiene semplicemente
esprimendo la vecchia nelle nuove coordinate
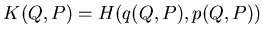 .
.
Nel seguito mi interesserò solo alle trasformazioni simplettiche,
che chiamerò, con abuso di linguaggio, canoniche.




Next: 8.2 Trasformazioni simplettiche indipendenti
Up: 8 Bignamino di Formalismo
Previous: 8 Bignamino di Formalismo
Indice
root
2001-04-02
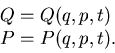
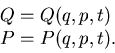
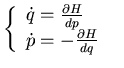 se e solo se
se e solo se 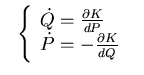 ?
?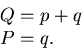
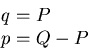
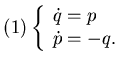
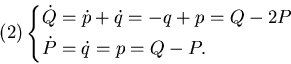
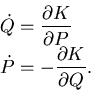
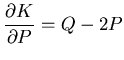 . Si ottiene
. Si ottiene
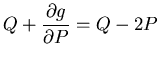 , quindi
, quindi ![]() in un sistema hamiltoniano,
mentre porta il sistema di hamiltoniana
in un sistema hamiltoniano,
mentre porta il sistema di hamiltoniana
![]() in un sistema
che non è hamiltoniano.
in un sistema
che non è hamiltoniano.