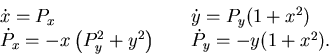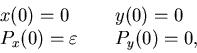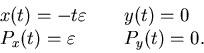


Next: 6 Alcuni esercizi svolti
Up: Esercitazioni di Meccanica Razionale
Previous: 4 Alcuni compiti d'esame
Indice
5 Soluzioni di alcuni compiti di esame
5.0.1 L,S,PO: Compito di Meccanica, febbraio '97
5.0.2 L,S,PO: Primo compito di esonero, a.a. 93-94.
La lagrangiana del sistema è:
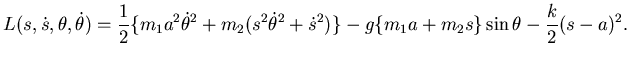 |
(5.1) |
Le soluzioni di equilibrio sono assegnate dagli zeri del sistema:
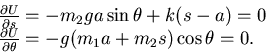 |
(5.2) |
Esse sono dunque:
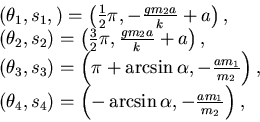 |
(5.3) |
ricordando che
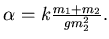 Ovviamente, le ultime due soluzioni esistono solo quando
Ovviamente, le ultime due soluzioni esistono solo quando
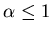 .
.
Per studiare la stabilità delle soluzioni studiamo
la matrice Hessiana di 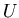 .
Ad essa è associata la forma quadratica:
.
Ad essa è associata la forma quadratica:
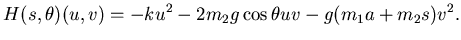 |
(5.4) |
Calcoliamola nelle varie posizioni di equilibrio.
Si ha:
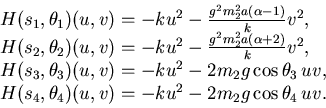 |
(5.5) |
Dunque finché
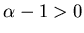 (rispettivamente
(rispettivamente 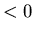 ), la posizione
), la posizione
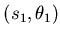 è instabile (risp. stabile). La posizione
è instabile (risp. stabile). La posizione
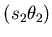 è sempre stabile. Quando esistono, cioé per
è sempre stabile. Quando esistono, cioé per
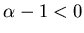 , le posizioni
, le posizioni
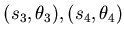 sono instabili.
sono instabili.
Osservazione: si osservi la conservazione del numero delle posizioni di
equilibro stabile, al variare di 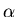 .
.
Le frequenze delle piccole oscillazioni sono determinate dagli
autovalori immaginari di 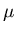 diag
diag
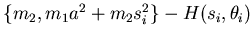 , dove si sono denotati con
, dove si sono denotati con
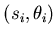 gli equilibri stabili. Si determinino quindi tali autovalori.
gli equilibri stabili. Si determinino quindi tali autovalori.
Passiamo alla quarta domanda. Il sistema di Lagrange è:
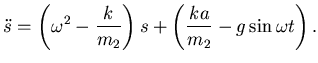 |
(5.6) |
Si tatta di un' equazione lineare con termine forzante dipendente dal tempo.
Possiamo riscriverla come un sistema del primo ordine. Introduciamo le matrici:
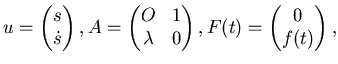 |
(5.7) |
dove
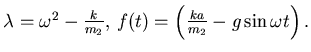 Si ha la seguente formula risolutiva:
Si ha la seguente formula risolutiva:
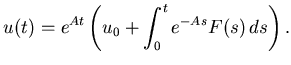 |
(5.8) |
Per quanto riguarda la matrice 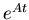 si ha:
si ha:
i)
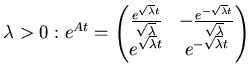 |
(5.9) |
ii)
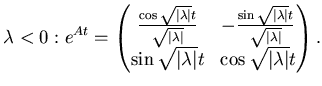 |
(5.10) |
Il lettore completi i calcoli.
5.0.3 CR,L,S Compito di Meccanica Razionale, 6/6/'96, I appello, sess. estiva.
appello, sess. estiva.
1)
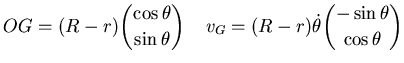 |
(5.11) |
La condizione di puro rotolamento è:
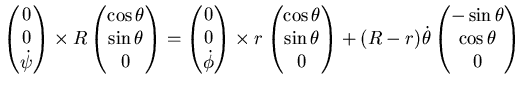 |
(5.12) |
cioé:
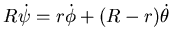 ,
che è integrabile:
,
che è integrabile:
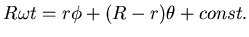 .
.
2) Vale:
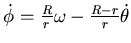 .
.
Energia della circonferenza:
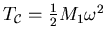 .
.
Energia cinetica del disco:
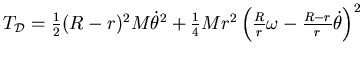 .
.
Energia potenziale:
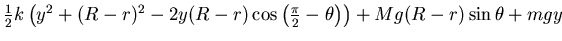 .
.
A meno di derivate totali rispetto al tempo, la lagrangiana
é:
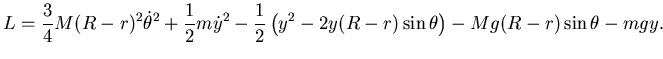 |
(5.13) |
3)
Equilibri:
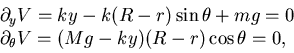 |
(5.14) |
da cui si ricava:
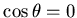 , oppure
, oppure
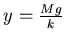 .
Quindi le soluzioni stazionarie sono:
.
Quindi le soluzioni stazionarie sono:
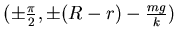 e, indicato
e, indicato
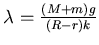 , se
, se 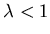 :
:
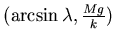 ,
,
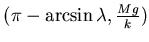 .
.
4)
Stabilità: l'hessiano dell'energia potenziale è
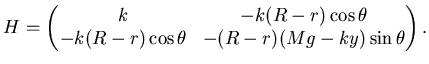 |
(5.15) |
Per
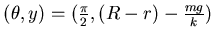 :
:
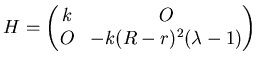 |
(5.16) |
dunque è stabile se
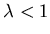 , instabile se
, instabile se 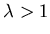 .
.
Per
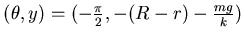 :
:
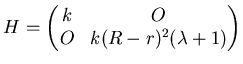 |
(5.17) |
dunque è stabile per tutti i valori di 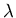 .
.
Per 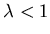 ,
,
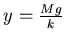 :
:
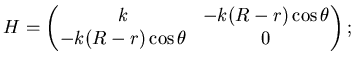 |
(5.18) |
det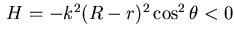 , dunque sono entrambe
instabili.
, dunque sono entrambe
instabili.
Per 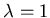 :
:
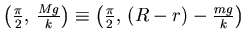 che è instabile, altrimenti l'energia potenziale avrebbe due
minimi stretti come unici punti critici.
che è instabile, altrimenti l'energia potenziale avrebbe due
minimi stretti come unici punti critici.
4)
Le Equazioni del moto sono:
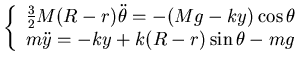 |
(5.19) |
ora
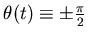 risolve identicamente
la prima equazione; dunque il moto del punto
risolve identicamente
la prima equazione; dunque il moto del punto 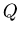 è dato da:
è dato da:
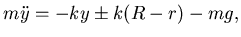 |
(5.20) |
che è un moto armonico intorno agli equilibri
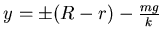 .
.
5.0.4 CR,L,S Compito di Meccanica Razionale, sess. estiva
(Pulvirenti)
La condizione di puro rotolamento fornisce per il moto del baricentro:
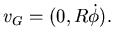 |
(5.21) |
e quindi, viste le condizioni iniziali:
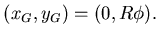 |
(5.22) |
Il punto  ha coordinate:
ha coordinate:
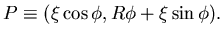 |
(5.23) |
La Lagrangiana del sistema 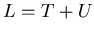 è:
è:
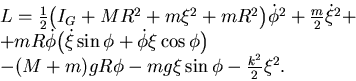 |
(5.24) |
Le posizioni di equilibrio sono gli zeri del gradiente del potenziale 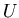
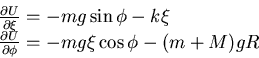 |
(5.25) |
Pertanto gli equilibri esistono solo se :
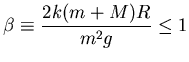 |
(5.26) |
e sono:
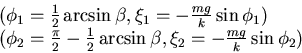 |
(5.27) |
Lo Hessiano del potenziale è dato da:
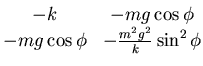 |
(5.28) |
Dunque la sua traccia,in entrambe le posizioni di equilibrio,
é negativa, cioé la somma degli autovalori dello Hessiano è negativa.
Il determinante  vale:
vale:
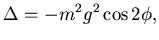 |
(5.29) |
Quindi, finché 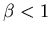 ,
,  è negativo se
è negativo se
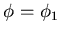 (e
quindi equilibrio instabile), positivo se
(e
quindi equilibrio instabile), positivo se
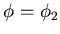 (e quindi
equilibrio stabile). Per
(e quindi
equilibrio stabile). Per 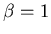 si ha un caso critico. Infine, alla
quarta domanda si risponde osservando che in questo caso il moto è
uniformemente accelerato.
si ha un caso critico. Infine, alla
quarta domanda si risponde osservando che in questo caso il moto è
uniformemente accelerato.
5.0.5 CR,L,S Compito sessione estiva a.a. 93-94
5.0.6 CR,L,S,PO: Compito di Meccanica Razionale del 6.10.94
La lagrangiana del sistema è:
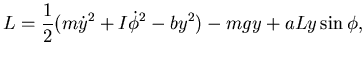 |
(5.30) |
dove si è posto
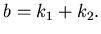
Equilibri. Si debbono determinare gli zeri del campo gradiente:
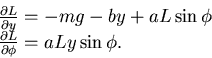 |
(5.31) |
Si hanno le seguenti soluzioni:
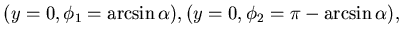 |
(5.32) |
sse
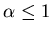 .Inoltre, si hanno le restanti soluzioni, per ogni valore
di
.Inoltre, si hanno le restanti soluzioni, per ogni valore
di 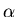 :
:
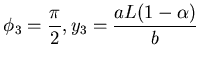 |
(5.33) |
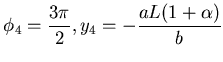 |
(5.34) |
.
Stabilità. Calcolato 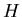 , lo Hessiano di L rispetto a
, lo Hessiano di L rispetto a 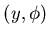 , si
ha:
, si
ha:
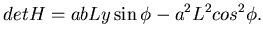 |
(5.35) |
La traccia di 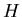 è:
è:
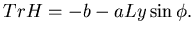 |
(5.36) |
Di conseguenza, detti
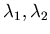 gli autovalori di
gli autovalori di 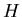 ,
negli equilibri
,
negli equilibri
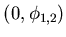 si ha:
si ha:
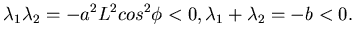 |
(5.37) |
Dunque si hanno due equilibri instabili, per
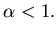 In
In
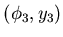 , si ha:
, si ha:
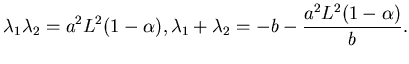 |
(5.38) |
Dunque, l'equilibrio è stabile se 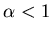 , se
, se
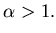 Finalmente, si constata facilmente che
Finalmente, si constata facilmente che
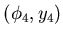 è sempre
stabile se
è sempre
stabile se
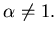
Consideriamo quindi la lagrangiana quadratica
ottenuta da L, tenendo in conto solo i termini di ordine 2 inclusi,
relativamente all'equilibrio
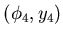 . Posto
. Posto
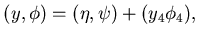 |
(5.39) |
si ha:
![$\displaystyle L_{[2]} = {1\over 2}\left( m\dot \eta^{2} + I \dot \psi^{2} -b \eta^{2} - {a^{2}L^{2}(1+\alpha)\over b}\psi^{2} \right) .$](img679.png) |
(5.40) |
Il corrispondente sistema Lagrangiano si separa in due
sottosistemi:precisamente i sistemi due oscillatori armonici disaccoppiati,
quello in 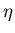 di frequenza
di frequenza
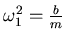 , quello in
, quello in 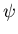 di frequenza
di frequenza
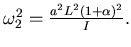
Consideriamo l'ultima domanda. Posto 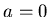 nell'espressione di
nell'espressione di 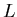 , il
problema si riduce a due problemi lagrangiani separati, il primo di
Lagrangiana:
, il
problema si riduce a due problemi lagrangiani separati, il primo di
Lagrangiana:
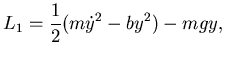 |
(5.41) |
il secondo di lagrangiana
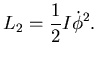 |
(5.42) |
Il primo problema ha solo moti periodici, e precisamente oscillazioni
lineari attorno all'equilibrio
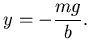 |
(5.43) |
Il secondo problema fornisce
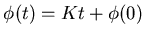 , con
, con 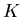 costante
arbitraria.
costante
arbitraria.
5.0.7 CR,L,S,PO Compito del 20.6.94 (Marchioro)
5.0.8 CR,L,S,PO: Compito del 11.7.94 (Marchioro)
5.0.9 CR,L,S,PO Esonero di Meccanica Razionale del 14-5-90
5.0.10 CR,LS,PO Esonero di Meccanica Razionale del 14-5-90
5.0.11 L,RU Compito di Meccanica del 23.2.1995
5.0.12 L,RU,N: Primo compito di esonero, a.a.94-95.
1) Il sistema è invariante per rotazioni attorno all'asse perpendicolare
al piano
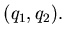 Pertanto si conserva la componente lungo questo
asse del momento angolare:
Pertanto si conserva la componente lungo questo
asse del momento angolare:
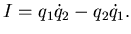 |
(5.44) |
Consideriamo i livelli
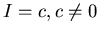 . Introduciamo le coordinate polari:
. Introduciamo le coordinate polari:
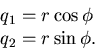 |
(5.45) |
La Lagrangiana 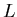 si riscrive in queste coordinate:
si riscrive in queste coordinate:
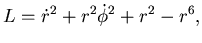 |
(5.46) |
l'integrale primo 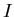 :
:
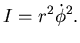 |
(5.47) |
Il sistema Lagrangiano ristretto sul livello 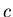 è dato dalla Lagrangiana:
è dato dalla Lagrangiana:
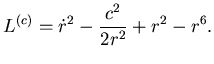 |
(5.48) |
La funzione energia potenziale
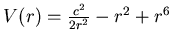 ha un solo minimo e costituisce una barriera per il punto
ha un solo minimo e costituisce una barriera per il punto 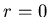 : per ogni
valore di
: per ogni
valore di 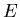 ,
,
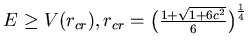 , si hanno due radici
, si hanno due radici
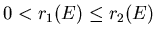 dell'equazione
dell'equazione 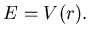 Le radici sono distinte se
Le radici sono distinte se
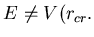 Tutti i moti sono quindi limitati e perció periodici.
Tutti i moti sono quindi limitati e perció periodici.
(2). L'invarianza della retta è ovvia, corrisponde a 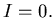 Il
sistema di Lagrange corrisponde sulla retta al sistema:
Il
sistema di Lagrange corrisponde sulla retta al sistema:
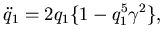 |
(5.49) |
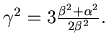
Si tratta di un problema Lagrangiano con potenziale:
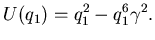 |
(5.50) |
Il potenziale ha tre punti critici,
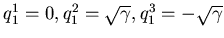 .
.
Il punto 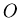 è un punto di equilibrio instabile,
è un punto di equilibrio instabile,
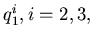 sono stabili. Si tratta di una doppia buca. Tutte le soluzioni
sono limitate. La separatrice ha equazione:
sono stabili. Si tratta di una doppia buca. Tutte le soluzioni
sono limitate. La separatrice ha equazione:
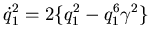 |
(5.51) |
5.0.13 CR,L,RU: Compito di Meccanica Razionale del 26.2.96
Siano 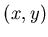 le coordinate del centra del disco
le coordinate del centra del disco 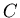 , relativamente ad un
sistema piano fisso
, relativamente ad un
sistema piano fisso 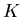 . Denotiamo con
. Denotiamo con 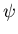 l'angolo che un sistema
l'angolo che un sistema 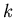 , di
coordinate
, di
coordinate
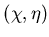 , origine in
, origine in 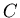 , di assi solidali al disco forma col
sistema fisso
, di assi solidali al disco forma col
sistema fisso 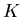 . Sia poi
. Sia poi  l'angolo che individua il punto
l'angolo che individua il punto  sul bordo
del disco, e precisamente l'angolo che
sul bordo
del disco, e precisamente l'angolo che 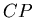 forma con l'asse parallelo
all'asse
forma con l'asse parallelo
all'asse 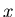 .
.
Si ha allora:
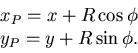 |
(5.52) |
La Lagrangiana del sistema è:
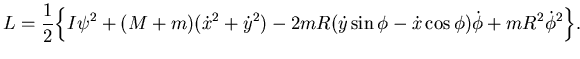 |
(5.53) |
Le coordinate
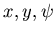 sono cicliche, e pertanto si hanno tre integrali
primi del moto:
sono cicliche, e pertanto si hanno tre integrali
primi del moto:
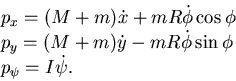 |
(5.54) |
Possiamo ottenere il moto del sistema considerando il livello
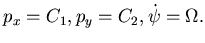
La lagrangiana ridotta diviene allora banalmente equivalente
alla Lagrangiana assegnata dalla sola eneria cinetica
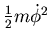 .
In conclusione, il moto del sistema è assegnato da:
.
In conclusione, il moto del sistema è assegnato da:
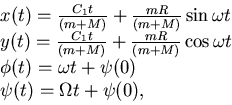 |
(5.55) |
essendo
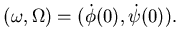
Il compito puó essere variato, aggiungendo la considerazione di una forza
agente su  , dipendente solo dall'angolo
, dipendente solo dall'angolo 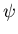 . Nella Lagrangiana si ha
allora una presenza del potenziale
. Nella Lagrangiana si ha
allora una presenza del potenziale 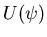 che non impedisce la presenza
dei tre integrali primi citati. Il problema si riconduce ad un problema ad un
solo grado di libertà.
che non impedisce la presenza
dei tre integrali primi citati. Il problema si riconduce ad un problema ad un
solo grado di libertà.
5.0.14 CR,L,S,RU Compito sessione estiva a.a. 93-94
5.0.15 L,S,H Secondo appello Meccanica Razionale a.a. 93-94.
5.0.16 L,S,N
Prima domanda. La simmetria del potenziale si puó meglio rappresentare
utilizzando coordinate cilindriche:
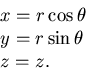 |
(5.56) |
In tale sistema di coordinate, il gruppo diventa:
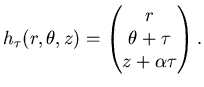 |
(5.57) |
Si ha allora:
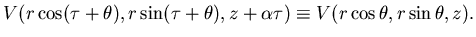 |
(5.58) |
Deve allora aversi, posto
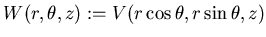 :
:
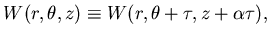 |
(5.59) |
e perció:
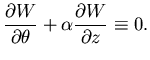 |
(5.60) |
Allora si ha:
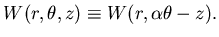 |
(5.61) |
La Lagrangiana è:
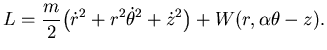 |
(5.62) |
Il gruppo ad un parametro è una rotazione nel piano 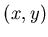 accoppiata ad una
traslazione lungo l'asse
accoppiata ad una
traslazione lungo l'asse 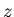 ; palesemente è un'isometria in
; palesemente è un'isometria in
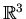 e lascia
dunque invariata l'energia cinetica.
e lascia
dunque invariata l'energia cinetica.
L'integrale primo di Noether è:
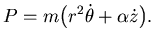 |
(5.63) |
Possiamo adattare ancora le coordinate alla simmetria, introducendo:
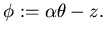 |
(5.64) |
La lagrangiana in
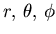 è:
è:
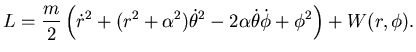 |
(5.65) |
Con questa scelta di coordinate la variabile 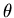 è ciclica;
per ottenere la Lagrangiana ridotta procediamo con iil metodo di Routh,
operiamo, cioé, la trasformata di Legendere nella variabile
è ciclica;
per ottenere la Lagrangiana ridotta procediamo con iil metodo di Routh,
operiamo, cioé, la trasformata di Legendere nella variabile
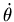 :
:
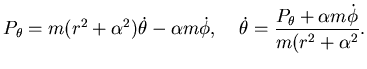 |
(5.66) |
La Lagrangiana cercata è
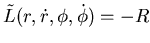 :
:
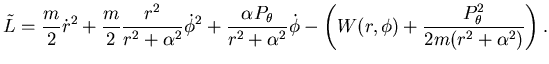 |
(5.67) |
dove
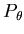 è una costante.
Si è dunque eliminata un grado di libertà, ottenendo l'energia potenziale
efficace:
è una costante.
Si è dunque eliminata un grado di libertà, ottenendo l'energia potenziale
efficace:
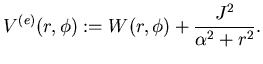 |
(5.68) |
Si osservi che la sostituzione dell'integrale primo nell'espressione
dell'energia totale, dà l'energia associata alla lagrangiana 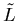 :
:
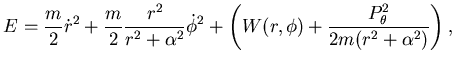 |
(5.69) |
ma essendo 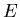 l'energia di un sistema a due gradi di libertà,
non si puó
da essa risalire all'espressione corretta di
l'energia di un sistema a due gradi di libertà,
non si puó
da essa risalire all'espressione corretta di 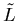 , che infatti contiene
un termine lineare in
, che infatti contiene
un termine lineare in 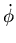 , che non dà contributo all'energia.
, che non dà contributo all'energia.
Per ovviare alla difficoltà formale
data dalla presenza di termini non
diagonali nell'energia cinetica
(e cioé del termine in
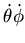 ),
si puo' procedere nel modo seguente: detta
),
si puo' procedere nel modo seguente: detta
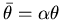 ,
si vogliono scegliere
,
si vogliono scegliere
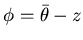 e
e 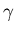 come nuove variabili, con
come nuove variabili, con 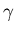 da determinare, in modo che
il termine cinetico
da determinare, in modo che
il termine cinetico
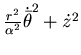 resti
diagonale. La scelta giusta è
resti
diagonale. La scelta giusta è
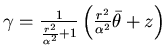 (stiamo procedento in
analogia all'eliminazione del moto del baricentro nel problema dei due corpi:
(stiamo procedento in
analogia all'eliminazione del moto del baricentro nel problema dei due corpi:
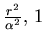 giocano il ruolo delle masse,
giocano il ruolo delle masse,
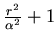 della massa totale e
della massa totale e
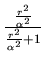 della massa ridotta). Si ottiene:
della massa ridotta). Si ottiene:
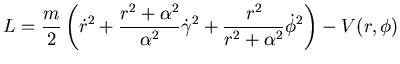 |
(5.70) |
.
La lagrangiana ridotta è dunque:
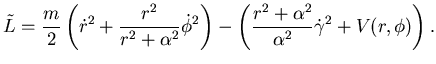 |
(5.71) |
Seconda domanda.I punti critici dell'energia potenziale efficace sono dati
dalle soluzioni del sistema:
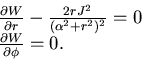 |
(5.72) |
Se
 è una soluzione, allora si ricava un moto
uniforme:
è una soluzione, allora si ricava un moto
uniforme:
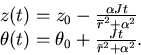 |
(5.73) |
Terza domanda.
Gli equilibri sono assegnati dalle soluzioni del sistema:
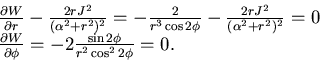 |
(5.74) |
Consideriamo solo il caso
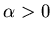 , lasciando al lettore il completamento
della discussione. Si hanno soluzioni reali solo se
, lasciando al lettore il completamento
della discussione. Si hanno soluzioni reali solo se 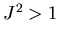 . Fissiamoci
sul caso
. Fissiamoci
sul caso 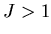 . Si ha:
. Si ha:
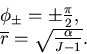 |
(5.75) |
Il lettore completi l'analisi costruendo la matrice Hessiana di 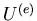 , e
computandola negli equilibri.
, e
computandola negli equilibri.
5.0.17 L,RU,H,HJ,AA
Compito di Meccanica Razionale,
9/7/'96, II appello, sess. estiva
appello, sess. estiva
1) La Lagrangiana nelle variabili 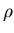 e
e 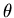 è:
è:
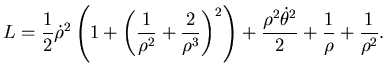 |
(5.76) |
L'Hamiltoniana, negli impulsi
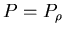 ,
,
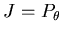 è:
è:
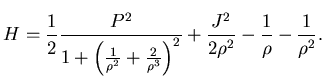 |
(5.77) |
2) Gli integrali primi sono l'energia e il momento
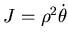 .
.
3) Il moto si puó ricondurre ad un moto unidimensionale di
energia potenziale efficace
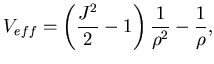 |
(5.78) |
che è limitato dal basso se 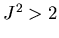 .
.
Se 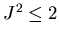 il tempo di arrivo in
il tempo di arrivo in 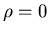 che corrisponde a
che corrisponde a
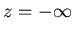 , è finito, dunque se
, è finito, dunque se 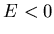 o se
o se
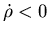 il moto esplode in tempo finito.
il moto esplode in tempo finito.
Cosidero dunque solo 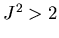 :
Il moto è limitato se
:
Il moto è limitato se 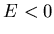 , illimitato
se
, illimitato
se 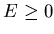 .
.
4) L'espressione dell' orbita in forma implicita si ricava
da:
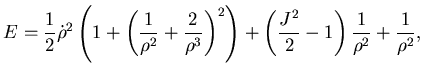 |
(5.79) |
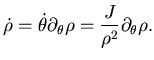 |
(5.80) |
Dunque l'angolo cercato è:
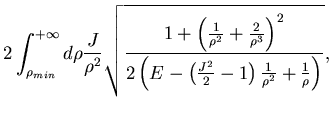 |
(5.81) |
dove
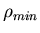 è la minima distanza dall'asse
è la minima distanza dall'asse
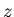 che il punto raggiunge.
che il punto raggiunge.
Tale angolo è finito se 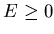 .
.
5) L'equazione di H-J è resolubile per separazione di
variabili.
6) Il moto è descrivibile in variabili azione angolo
nella regione dello spazio delle fasi
in cui 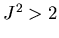 e
e 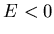 .
.
5.0.18 CR,L,RU,H,HJ
Compito di Meccanica Razionale,
24/9/'96, I appello, sess. autunnale
appello, sess. autunnale
1) Siano 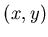 le coordinate di
le coordinate di  nel sistema fisso, e
nel sistema fisso, e
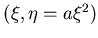 nel sistema solidale alla guida.
nel sistema solidale alla guida.
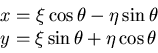 |
(5.82) |
.
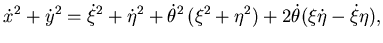 |
(5.83) |
dove:
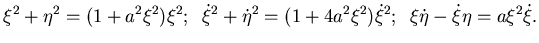 |
(5.84) |
La Lagrangiana è:
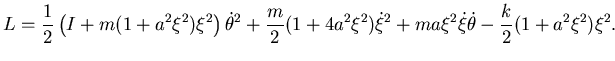 |
(5.85) |
La variabile 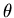 è ciclica, si conserva oltre all'energia
il momento della quantità di moto:
è ciclica, si conserva oltre all'energia
il momento della quantità di moto:
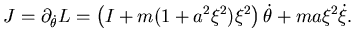 |
(5.86) |
2) Dall'espressione del momento:
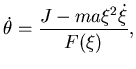 |
(5.87) |
dove
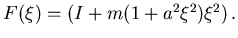 Sostituendo nell'espressione dell'energia si ottiene:
Sostituendo nell'espressione dell'energia si ottiene:
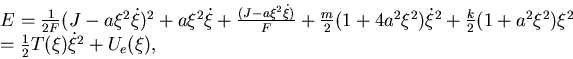 |
(5.88) |
dove:
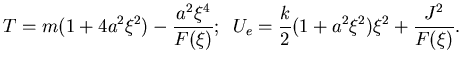 |
(5.89) |
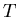 è una funzione strettamente positiva, l'energia potenziale
efficace ha un unico punto critico (stabile) in 0 se
è una funzione strettamente positiva, l'energia potenziale
efficace ha un unico punto critico (stabile) in 0 se
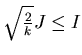 .
Altrimenti 0 è instabile e compaiono i due equilibri stabili
simmetrici
.
Altrimenti 0 è instabile e compaiono i due equilibri stabili
simmetrici 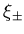 , uniche due soluzioni di
, uniche due soluzioni di
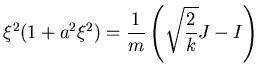 |
(5.90) |
(
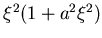 è una funzione strettamente convessa).
è una funzione strettamente convessa).
3) Dall'analisi qualitativa, si ottiene che 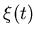 è
sempre periodica se non è costante.
Se
è
sempre periodica se non è costante.
Se 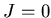 ,
,
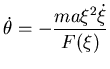 |
(5.91) |
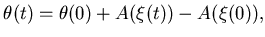 |
(5.92) |
dove 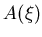 è la
primitiva di
è la
primitiva di
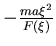 . Quindi
il moto complessivo è periodico dello stesso periodo di
. Quindi
il moto complessivo è periodico dello stesso periodo di
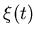 .
.
5.0.19 CR,L,RU,H,HJ,AA
Compito di Meccanica Razionale,
8/10/'96, II appello, sess. autunnale
appello, sess. autunnale
Indica con  l'angolo sul piano
l'angolo sul piano
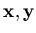 che il disco forma
con l'asse delle
che il disco forma
con l'asse delle
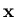 , con
, con
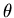 l'angolo che
l'angolo che 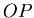 forma con il piano
forma con il piano
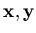 , con
, con
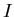 e
e 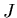 i momenti di inerzia del disco rispetto all'asse
i momenti di inerzia del disco rispetto all'asse
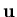 e all'asse
e all'asse
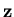 rispettivamente.
Le coordinate cartesiane del punto sono:
rispettivamente.
Le coordinate cartesiane del punto sono:
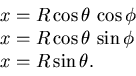 |
(5.93) |
Dunque:
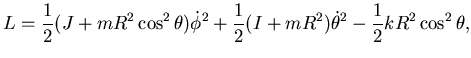 |
(5.94) |
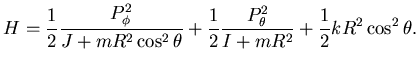 |
(5.95) |
Il sistema è invariante per rotazioni intorno all'asse
delle
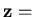 , dunque si conserva l'energia meccanica
e il momento della quantità di moto rispetto a questo asse:
, dunque si conserva l'energia meccanica
e il momento della quantità di moto rispetto a questo asse:
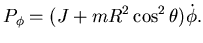 |
(5.96) |
Ottieni un problema unidimensionale sostituendo a
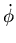 la sua espressione in termini di
la sua espressione in termini di 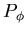 nell'espressione dell'energia totale:
nell'espressione dell'energia totale:
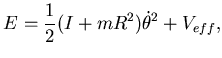 |
(5.97) |
dove
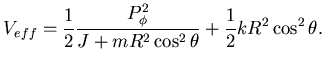 |
(5.98) |
Derivando l'energia potenziale nella variabile 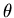 ,
ottieni:
,
ottieni:
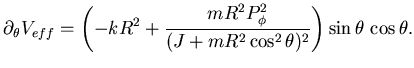 |
(5.99) |
Il problema e' simmetrico rispetto alle trasformazioni
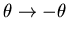 , e
, e
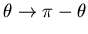 ,
quindi ti limiti a studiarlo tra
,
quindi ti limiti a studiarlo tra
![$ [0, \frac \pi2]$](img813.png) .
I valori 0 e
.
I valori 0 e
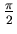 sono soluzioni stazionarie per tutti i
valori dei parametri. Inoltre esiste un'altra soluzione
se
sono soluzioni stazionarie per tutti i
valori dei parametri. Inoltre esiste un'altra soluzione
se
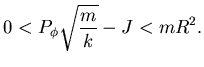 |
(5.100) |
Graficando l'energia potenziale efficace, ottieni che
la posione
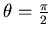 è stabile fino a che
è stabile fino a che
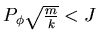 , mentre
, mentre 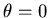 è instabile.
Appena si biforca, cioé quando
è instabile.
Appena si biforca, cioé quando
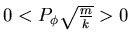 ,
,
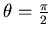 diventa instabile; quando la soluzione
intermedia raggiunge
diventa instabile; quando la soluzione
intermedia raggiunge 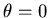 , cioé quando
, cioé quando
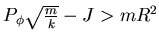 ,
, 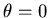 diventa stabile.
diventa stabile.
5.0.20 TC
5.0.21 TC
5.0.22 TC,AA,P Secondo compito di esonero a.a.94.
Cerca
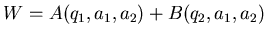 (
(
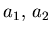 sono i nuovi
impulsi).
L'equazione da risolvere è:
sono i nuovi
impulsi).
L'equazione da risolvere è:
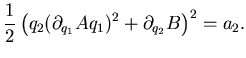 |
(5.101) |
Stai cercando 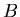 in modo che non dipenda da
in modo che non dipenda da 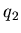 , ma solo da
, ma solo da 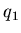 .
Dall'equazione puoi ricavare:
.
Dall'equazione puoi ricavare:
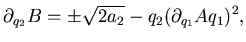 |
(5.102) |
peró in questa espressione
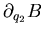 dipendende da
dipendende da 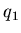 , e da
, e da 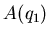 ;
l'unica possibilità che ho è dunque che la combinazione
;
l'unica possibilità che ho è dunque che la combinazione
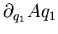 non dipenda da
non dipenda da 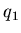 , cioé:
, cioé:
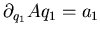 , ovvero
, ovvero
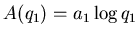 .
A questo punto posso risolvere anche l'equazione in
.
A questo punto posso risolvere anche l'equazione in  infatti
infatti
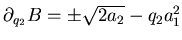 è una funzione
della sola
è una funzione
della sola  e dei nuovi impulsi.
Riassumendo, ottieni:
e dei nuovi impulsi.
Riassumendo, ottieni:
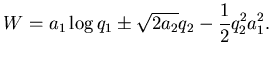 |
(5.103) |
La traformazione generata da 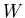 è:
è:
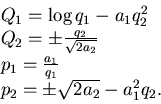 |
(5.104) |
Le equazioni del moto per l'hamiltoniana
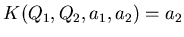 sono:
sono:
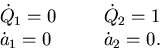 |
(5.105) |
Quindi
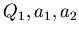 sono costanti e
sono costanti e
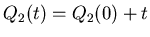 .
Tornando alle vecchie variabili
ottieni:
.
Tornando alle vecchie variabili
ottieni:
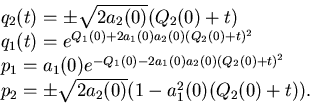 |
(5.106) |
Il segno 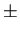 lo determini a seconda del segno di
lo determini a seconda del segno di
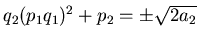 .
.
Nella soluzione compaiono
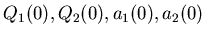 che determini
imponendo i dati iniziali.
che determini
imponendo i dati iniziali.
5.0.23 H,HJ,AA,S: II esonero 10/5/'96
a) Cerca una soluzione dell'equazione caratteristica di Hamilton-Jacobi
del tipo:
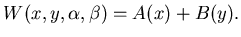 |
(5.107) |
Sostituendo:
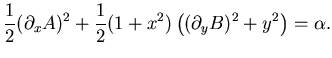 |
(5.108) |
Ottengo la soluzione ponendo
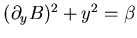 :
:
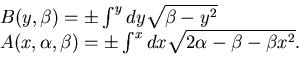 |
(5.109) |
b) La regione dello spazio delle fasi in cui il moto
é multiperiodico è data da 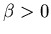 ,
,
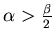 .
.
c) Devi calcolare:
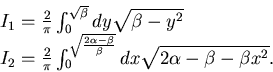 |
(5.110) |
Ricorda che
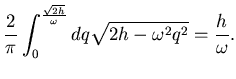 |
(5.111) |
Ottieni:
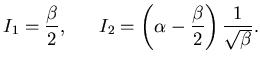 |
(5.112) |
Dunque la nuova Hamiltoniana è:
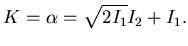 |
(5.113) |
Le frequenze:
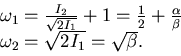 |
(5.114) |
d) Sostituendo il valore del dato iniziale in 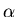 ,
, 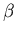 ottieni:
ottieni:
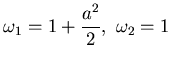 |
(5.115) |
Il moto è periodico se e solo se
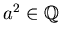 .
.
e) per 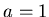 ,
,
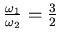 , dunque
, dunque
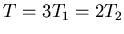 .
.
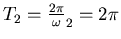 , dunque
, dunque 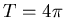 .
.
f) Le equazioni di Hamilton sono
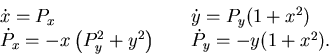 |
(5.116) |
Considera il dato iniziale:
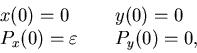 |
(5.117) |
che è una piccola perturbazione della posizione stazionaria.
La soluzione delle equazioni di Hamilton è:
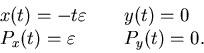 |
(5.118) |
Dunque la posizione di equilibio è instabile.
5.0.24 CR,H,HJ,P: Esonero di Meccanica Razionale
del 6-6-90
Subsections
- 5.0.1 L,S,PO: Compito di Meccanica, febbraio '97
- 5.0.2 L,S,PO: Primo compito di esonero, a.a. 93-94.
- 5.0.3 CR,L,S Compito di Meccanica Razionale, 6/6/'96, I
 appello, sess. estiva.
appello, sess. estiva.
- 5.0.4 CR,L,S Compito di Meccanica Razionale, sess. estiva
(Pulvirenti)
- 5.0.5 CR,L,S Compito sessione estiva a.a. 93-94
- 5.0.6 CR,L,S,PO: Compito di Meccanica Razionale del 6.10.94
- 5.0.7 CR,L,S,PO Compito del 20.6.94 (Marchioro)
- 5.0.8 CR,L,S,PO: Compito del 11.7.94 (Marchioro)
- 5.0.9 CR,L,S,PO Esonero di Meccanica Razionale del 14-5-90
- 5.0.10 CR,LS,PO Esonero di Meccanica Razionale del 14-5-90
- 5.0.11 L,RU Compito di Meccanica del 23.2.1995
- 5.0.12 L,RU,N: Primo compito di esonero, a.a.94-95.
- 5.0.13 CR,L,RU: Compito di Meccanica Razionale del 26.2.96
- 5.0.14 CR,L,S,RU Compito sessione estiva a.a. 93-94
- 5.0.15 L,S,H Secondo appello Meccanica Razionale a.a. 93-94.
- 5.0.16 L,S,N
- 5.0.17 L,RU,H,HJ,AA
Compito di Meccanica Razionale,
9/7/'96, II
 appello, sess. estiva
appello, sess. estiva
- 5.0.18 CR,L,RU,H,HJ
Compito di Meccanica Razionale,
24/9/'96, I
 appello, sess. autunnale
appello, sess. autunnale
- 5.0.19 CR,L,RU,H,HJ,AA
Compito di Meccanica Razionale,
8/10/'96, II
 appello, sess. autunnale
appello, sess. autunnale
- 5.0.20 TC
- 5.0.21 TC
- 5.0.22 TC,AA,P Secondo compito di esonero a.a.94.
- 5.0.23 H,HJ,AA,S: II esonero 10/5/'96
- 5.0.24 CR,H,HJ,P: Esonero di Meccanica Razionale
del 6-6-90



Next: 6 Alcuni esercizi svolti
Up: Esercitazioni di Meccanica Razionale
Previous: 4 Alcuni compiti d'esame
Indice
root
2001-04-02
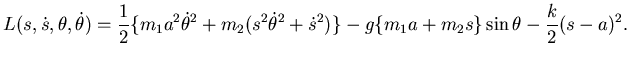
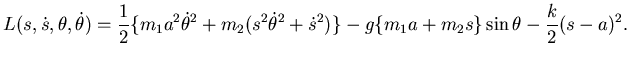
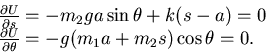
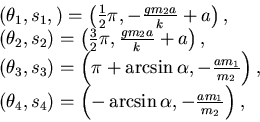
![]() .
Ad essa è associata la forma quadratica:
.
Ad essa è associata la forma quadratica:
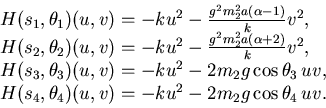
![]() .
.
![]() diag
diag
![]() , dove si sono denotati con
, dove si sono denotati con
![]() gli equilibri stabili. Si determinino quindi tali autovalori.
gli equilibri stabili. Si determinino quindi tali autovalori.
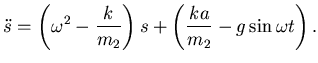
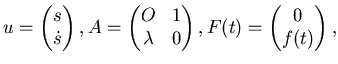
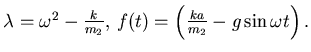 Si ha la seguente formula risolutiva:
Si ha la seguente formula risolutiva:
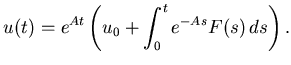
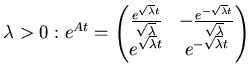
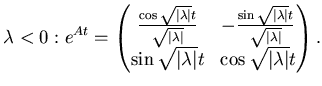
![]() .
.
![]() .
.
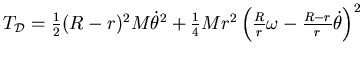 .
.
![]() .
.
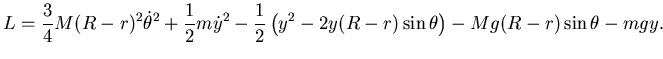
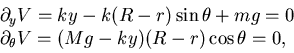
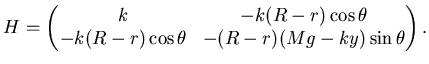
![]() :
:
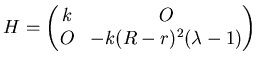
![]() :
:
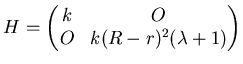
![]() ,
,
![]() :
:
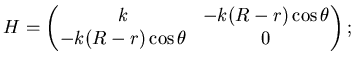
![]() :
:
![]() che è instabile, altrimenti l'energia potenziale avrebbe due
minimi stretti come unici punti critici.
che è instabile, altrimenti l'energia potenziale avrebbe due
minimi stretti come unici punti critici.
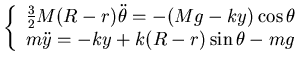
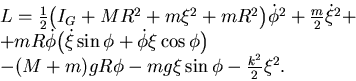
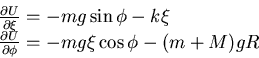
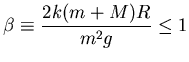
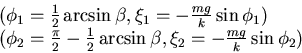
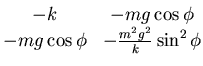
![]() vale:
vale:
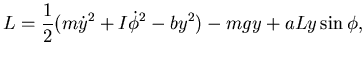
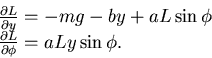
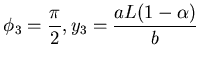
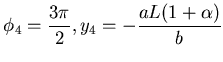
![]() , lo Hessiano di L rispetto a
, lo Hessiano di L rispetto a ![]() , si
ha:
, si
ha:
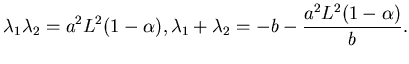
![]() . Posto
. Posto
![$\displaystyle L_{[2]} = {1\over 2}\left( m\dot \eta^{2} + I \dot \psi^{2} -b \eta^{2} - {a^{2}L^{2}(1+\alpha)\over b}\psi^{2} \right) .$](img679.png)
![]() nell'espressione di
nell'espressione di ![]() , il
problema si riduce a due problemi lagrangiani separati, il primo di
Lagrangiana:
, il
problema si riduce a due problemi lagrangiani separati, il primo di
Lagrangiana:
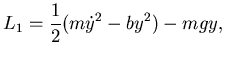
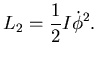
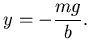
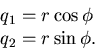
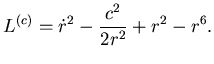
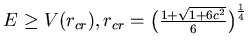 , si hanno due radici
, si hanno due radici
![]() Il
sistema di Lagrange corrisponde sulla retta al sistema:
Il
sistema di Lagrange corrisponde sulla retta al sistema:
![]() è un punto di equilibrio instabile,
è un punto di equilibrio instabile,
![]() sono stabili. Si tratta di una doppia buca. Tutte le soluzioni
sono limitate. La separatrice ha equazione:
sono stabili. Si tratta di una doppia buca. Tutte le soluzioni
sono limitate. La separatrice ha equazione:
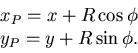
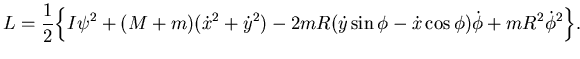
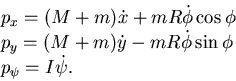
![]() .
In conclusione, il moto del sistema è assegnato da:
.
In conclusione, il moto del sistema è assegnato da:
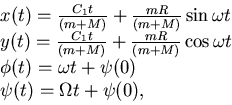
![]()
![]() , dipendente solo dall'angolo
, dipendente solo dall'angolo ![]() . Nella Lagrangiana si ha
allora una presenza del potenziale
. Nella Lagrangiana si ha
allora una presenza del potenziale ![]() che non impedisce la presenza
dei tre integrali primi citati. Il problema si riconduce ad un problema ad un
solo grado di libertà.
che non impedisce la presenza
dei tre integrali primi citati. Il problema si riconduce ad un problema ad un
solo grado di libertà.
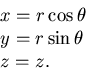
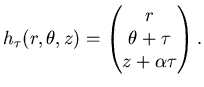
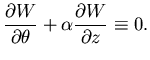
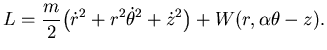
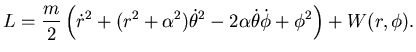
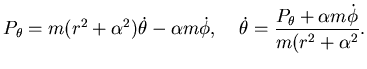
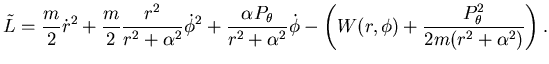
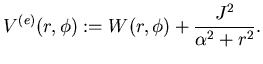
![]() :
:
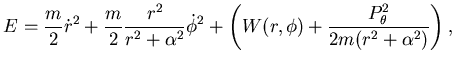
![]() ),
si puo' procedere nel modo seguente: detta
),
si puo' procedere nel modo seguente: detta
![]() ,
si vogliono scegliere
,
si vogliono scegliere
![]() e
e ![]() come nuove variabili, con
come nuove variabili, con ![]() da determinare, in modo che
il termine cinetico
da determinare, in modo che
il termine cinetico
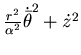 resti
diagonale. La scelta giusta è
resti
diagonale. La scelta giusta è
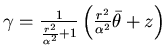 (stiamo procedento in
analogia all'eliminazione del moto del baricentro nel problema dei due corpi:
(stiamo procedento in
analogia all'eliminazione del moto del baricentro nel problema dei due corpi:
![]() giocano il ruolo delle masse,
giocano il ruolo delle masse,
![]() della massa totale e
della massa totale e
![]() della massa ridotta). Si ottiene:
della massa ridotta). Si ottiene:
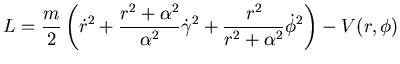
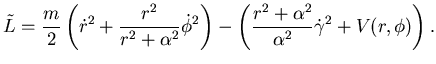
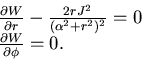
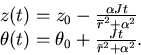
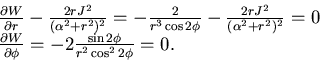
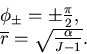
![]() e
e ![]() è:
è:
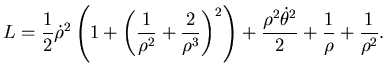
![]() ,
,
![]() è:
è:
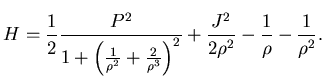
![]() .
.
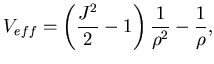
![]() il tempo di arrivo in
il tempo di arrivo in ![]() che corrisponde a
che corrisponde a
![]() , è finito, dunque se
, è finito, dunque se ![]() o se
o se
![]() il moto esplode in tempo finito.
il moto esplode in tempo finito.
![]() :
Il moto è limitato se
:
Il moto è limitato se ![]() , illimitato
se
, illimitato
se ![]() .
.
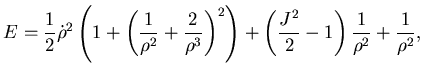
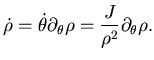
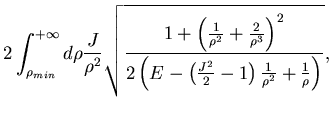
![]() .
.
![]() e
e ![]() .
.
![]() le coordinate di
le coordinate di ![]() nel sistema fisso, e
nel sistema fisso, e
![]() nel sistema solidale alla guida.
nel sistema solidale alla guida.
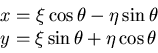
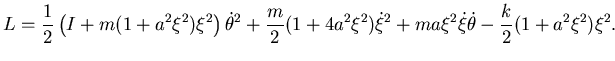
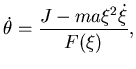
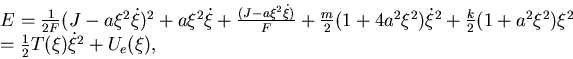
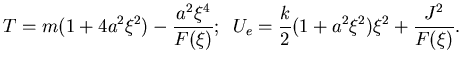
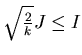 .
Altrimenti 0 è instabile e compaiono i due equilibri stabili
simmetrici
.
Altrimenti 0 è instabile e compaiono i due equilibri stabili
simmetrici 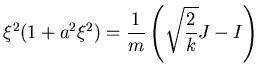
![]() è
sempre periodica se non è costante.
Se
è
sempre periodica se non è costante.
Se ![]() ,
,
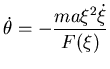
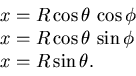
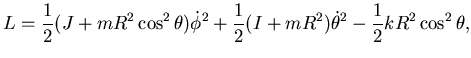
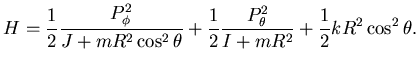
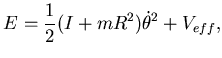
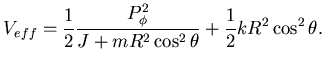
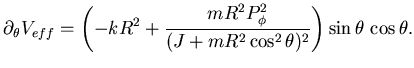
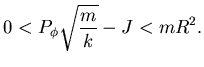
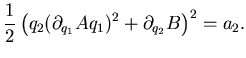
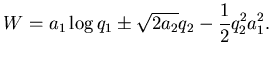
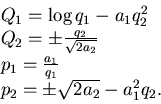
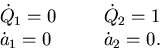
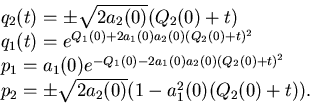
![]() che determini
imponendo i dati iniziali.
che determini
imponendo i dati iniziali.
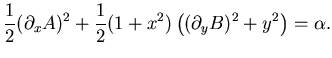
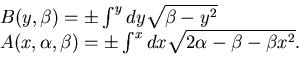
![]() ,
,
![]() .
.
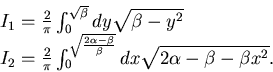
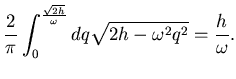
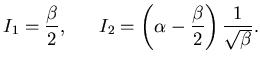
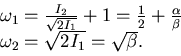
![]() ,
, ![]() ottieni:
ottieni:
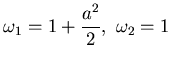
![]() ,
,
![]() , dunque
, dunque
![]() .
.
![]() , dunque
, dunque ![]() .
.