Un'asta omogenea di estremi ![]() e
e ![]() , massa
, massa ![]() , e lunghezza
, e lunghezza ![]() ,
é vincolata a muoversi su di un piano verticale
,
é vincolata a muoversi su di un piano verticale ![]() . Il suo estremo
. Il suo estremo
![]() è vincolato a muoversi su di una retta orizzontale
è vincolato a muoversi su di una retta orizzontale
![]() .
Inoltre,
.
Inoltre, ![]() ruota con velocità angolare costante
ruota con velocità angolare costante
![]() intorno all'asse verticale
intorno all'asse verticale ![]() , ortogonale a
, ortogonale a ![]() nel punto fisso
nel punto fisso
![]() .
.
Il punto ![]() dell'asta è richiamato dal punto
dell'asta è richiamato dal punto ![]() da una molla
ideale di costante elastica
da una molla
ideale di costante elastica ![]() .
.
Si introducano le coordinate lagrangiane
![]() distanza di
distanza di ![]() da
da ![]() , e
, e ![]() angolo tra la
direzione dell'asta e la direzione dell'asse
angolo tra la
direzione dell'asta e la direzione dell'asse ![]() .
.
1) Si scriva la Lagrangiana, e, considerando trascurabili gli effetti gravitazionali, e si determinino, conseguentemente, eventuali quantità conservate.
Sempre nell'approssimazione di cui al punto 1:
2) si determinino le soluzioni di equilibrio, al variare del
parametro
![]() ;
;
3) si discuta la stabilità delle soluzioni di equilibrio
al variare di ![]() ;
;
4) nel caso ![]() si calcolino le frequenze e i modi normali delle
piccole oscillazioni intorno alle posizioni di equilibrio stabile.
si calcolino le frequenze e i modi normali delle
piccole oscillazioni intorno alle posizioni di equilibrio stabile.
Nel piano verticale, si fissi un sistema di
riferimento inerziale ![]() , con
asse y orientato lungo la retta verticale
ascendente. Attorno al punto fisso
, con
asse y orientato lungo la retta verticale
ascendente. Attorno al punto fisso ![]() é libera di ruotare un'asta illimitata (senza peso).
Sia
é libera di ruotare un'asta illimitata (senza peso).
Sia ![]() la coordinata
sull'asta, scelta positiva alla destra di
la coordinata
sull'asta, scelta positiva alla destra di ![]() , e sia
, e sia ![]() l'angolo
(contato
in vero antiorario) che l'asta forma con l'asse
l'angolo
(contato
in vero antiorario) che l'asta forma con l'asse ![]() .
Sull'asta, in
.
Sull'asta, in ![]() ,
é fissato un punto
,
é fissato un punto ![]() di massa
di massa ![]() .
Inoltre, sull'asta, è libero di
scorrere un secondo punto materiale
.
Inoltre, sull'asta, è libero di
scorrere un secondo punto materiale ![]() , di massa
, di massa ![]() .
. ![]() è
richiamato da
è
richiamato da ![]() , con una forza elastica
, con una forza elastica
![]()
Prima domanda. Si scriva la lagrangiana del sistema.
Seconda domanda. Detto
![]() ,
discutere, al variare di questo parametro, le soluzioni
stazionarie del sistema
Lagrangiano, determinandone, per
,
discutere, al variare di questo parametro, le soluzioni
stazionarie del sistema
Lagrangiano, determinandone, per
![]() , le relative proprietà di
stabilità.
, le relative proprietà di
stabilità.
Terza domanda. Si determinino le frequenze delle "piccole oscillazioni" attorno alle posizioni di equilibrio stabili.
Quarta domanda. Si consideri
ora il seguente problema: l'asta gira con frequenza angolare costante
![]() attorno ad O. Si discuta il corrispondente problema ad un grado
di libertà .
attorno ad O. Si discuta il corrispondente problema ad un grado
di libertà .
Una circonferenza
![]() di raggio
di raggio ![]() e massa
e massa ![]() ruota con
velocità angolare costante
ruota con
velocità angolare costante ![]() in un piano verticale,
intorno al suo centro
in un piano verticale,
intorno al suo centro ![]() .
Sul suo bordo interno rotola senza strisciare un disco
.
Sul suo bordo interno rotola senza strisciare un disco
![]() di raggio
di raggio ![]() e massa
e massa ![]() . Il centro
. Il centro ![]() di tale disco
é richiamato da una molla elastica di costante
di tale disco
é richiamato da una molla elastica di costante ![]() , da un punto
materiale
, da un punto
materiale ![]() di massa
di massa ![]() , libero di scorrere sull'asse verticale
passante
per
, libero di scorrere sull'asse verticale
passante
per ![]() .
.
Indica con
![]() e
e ![]() gli angoli di rotazione propria
di
gli angoli di rotazione propria
di
![]() e
e
![]() rispettivamente, con
rispettivamente, con ![]() l'angolo
che
l'angolo
che ![]() forma con la direzione postitiva dell'asse orizzontale,
e con
forma con la direzione postitiva dell'asse orizzontale,
e con ![]() la quota del punto
la quota del punto ![]() rispetto a
rispetto a ![]() :
:
1) scrivi la condizione di puro rotolamento in termini di
![]() , e dimostra che è un vincolo
olonomo;
, e dimostra che è un vincolo
olonomo;
2) scrivi la Lagrangiana del sistema nelle variabili
lagrangiane
![]() ;
;
3) determina le soluzioni stazionare del relativo sistema di Lagrange,
al variare del parametro adimensionale
![]() ;
;
4) discuti la stabilità delle posizioni di equilibrio al variare di
![]() ;
;
5) determina le condizioni iniziali sul moto del baricentro ![]() del disco
del disco
![]() a cui corrispondono solo moti armonici
del punto
a cui corrispondono solo moti armonici
del punto ![]() .
.
Si consideri un sistema di riferimento piano inerziale di origine ![]() e assi
e assi
![]() , l'asse
, l'asse ![]() essendo scelto allineato con la verticale
ascendente. Un disco omogeneo, di raggio
essendo scelto allineato con la verticale
ascendente. Un disco omogeneo, di raggio ![]() , centro
, centro ![]() , e massa totale
, e massa totale ![]() ,
rotola senza strisciare (cioé puro rotolamento) lungo l'asse
,
rotola senza strisciare (cioé puro rotolamento) lungo l'asse ![]() . Lungo un
diametro del disco - di estremi
. Lungo un
diametro del disco - di estremi ![]() - è libero di scorrere senza attrito un
punto materiale di massa
- è libero di scorrere senza attrito un
punto materiale di massa ![]() . Tale punto è inoltre richiamato dal centro del
disco tramite una molla ideale di costante elastica
. Tale punto è inoltre richiamato dal centro del
disco tramite una molla ideale di costante elastica ![]() (
(![]() ).
Nell'istante iniziale il centro del disco si trova sull'asse
).
Nell'istante iniziale il centro del disco si trova sull'asse ![]() , il diametro
, il diametro
![]() è collineare all'asse
è collineare all'asse ![]() e
e
![]()
Si consideri un sistema solidale
![]() di assi incentrati in
di assi incentrati in ![]() , l'asse
, l'asse
![]() orientato come
orientato come ![]() . Si assumano come parametri Lagrangiani l'angolo
. Si assumano come parametri Lagrangiani l'angolo
![]() (contato in senso antiorario) che l'asse solidale
(contato in senso antiorario) che l'asse solidale ![]() forma con l'asse
delle
forma con l'asse
delle ![]() e l'ascissa
e l'ascissa ![]() del punto
del punto ![]() .
.
![]() domanda.
Si scriva la Lagrangiana del sistema.
domanda.
Si scriva la Lagrangiana del sistema.
![]() domanda. Si determinino le eventuali configurazioni di equilibrio.
domanda. Si determinino le eventuali configurazioni di equilibrio.
![]() domanda. Si discuta la stabilità delle soluzioni di equilibrio
determinate al punto
domanda. Si discuta la stabilità delle soluzioni di equilibrio
determinate al punto ![]() .
.
![]() domanda.
Si consideri ora un diverso problema, e cioé si consideri il punto
domanda.
Si consideri ora un diverso problema, e cioé si consideri il punto ![]() fissato nel centro. Descrivere il moto del sistema.
fissato nel centro. Descrivere il moto del sistema.
In un piano orizzontale sono poste due aste ![]() e
e ![]() di rispettive masse
di rispettive masse ![]() ed
ed ![]() (distribuzione di massa
omogenea) e lunghezze
(distribuzione di massa
omogenea) e lunghezze ![]() ed
ed ![]() . Le aste sono libere di ruotare
attorno ai rispettivi baricentri
. Le aste sono libere di ruotare
attorno ai rispettivi baricentri ![]() e
e ![]() , fissi nel piano,
con
, fissi nel piano,
con
![]() .
.
Sia ![]() un punto appartenente all'asta
un punto appartenente all'asta ![]() , giacente tra
, giacente tra ![]() e
e
![]() ,
, ![]() un punto appartenente all'asta
un punto appartenente all'asta ![]() ,
giacente tra
,
giacente tra
![]() e
e ![]() ,
,
![]() .
Tra i punti
.
Tra i punti ![]() e
e ![]() agisce una molla ideale, di costante elastica
agisce una molla ideale, di costante elastica
![]() . Si richiede:
. Si richiede:
1) scrivere la Lagrangiana del sistema;
2) determinare gli equilibri;
3) discutere la stabilità degli equilibri al variare del parametro
![]() in
in
![]() ;
;
4) considerato il sistema corrispondente a ![]() ,
si discuta il corrispondente sistema lagrangiano, mostrando che è
riconducibile ad un sistema ad un grado di libertà.
,
si discuta il corrispondente sistema lagrangiano, mostrando che è
riconducibile ad un sistema ad un grado di libertà.
In un piano verticale si adotta un sistema di riferimento inerziale
![]() , con
, con ![]() fisso, asse
fisso, asse ![]() orientato lungo la verticale ascendente.
Sull'asse
orientato lungo la verticale ascendente.
Sull'asse ![]() è libero di scorrere senza attrito il punto
è libero di scorrere senza attrito il punto ![]() di massa
m. Un'asta di estremi
di massa
m. Un'asta di estremi ![]() , massa M, lunghezza
, massa M, lunghezza ![]() è libera di
ruotare, senza attrito, attorno al suo punto medio, fissato in
è libera di
ruotare, senza attrito, attorno al suo punto medio, fissato in ![]() . Il
punto estremo
. Il
punto estremo ![]() (risp.
(risp. ![]() ) è richiamato dal punto
) è richiamato dal punto ![]() , tramite una molla
elastica ideale, di costante
, tramite una molla
elastica ideale, di costante ![]() (risp.
(risp. ![]() ).
Si assuma
).
Si assuma
![]() .
.
(I). Si scriva la Lagrangiana del sistema e si determinino le
configurazioni di equilibrio al variare del parametro
![]() .
.
(II). Si discuta la stabilità degli equilibri al variare del parametro
![]() in
in
![]() .
.
(III). Si studi il sistema Lagrangiano ottenuto per linearizzazione
attorno alla posizione di equilibrio che è stabile per ogni ![]() ,
nell'intervallo predetto.
,
nell'intervallo predetto.
(IV). Si assuma ora ![]() Si determinino i moti del
corrispondente sistema lagrangiano.
Si determinino i moti del
corrispondente sistema lagrangiano.
Una sbarra rigida omogena pesante ![]() di lunghezza
di lunghezza ![]() e massa
e massa ![]() è posta in un piano verticale ed è libera di ruotare
senza attrito attorno al suo estremo
è posta in un piano verticale ed è libera di ruotare
senza attrito attorno al suo estremo ![]() . Per l'altro estremo
. Per l'altro estremo ![]() passa una guida di massa trascurabile ortogonale alla sbarra.
Lungo tale guida si muove senza attrito un punto materiale pesante
passa una guida di massa trascurabile ortogonale alla sbarra.
Lungo tale guida si muove senza attrito un punto materiale pesante ![]() di massa
di massa ![]() . Esso è soggetto oltre al peso ad una forza elastica
. Esso è soggetto oltre al peso ad una forza elastica
![]() ,
, ![]() .
.
Scegliamo come variabili lagrangiane l'angolo ![]() che la sbarra
forma con la verticale discendente e l'ascissa
che la sbarra
forma con la verticale discendente e l'ascissa ![]() del punto
del punto
![]() lungo la guida.
lungo la guida.
1) Scrivere le equazioni del moto del sistema.
2) Trovare le posizioni di equilibrio e discuterne il numero e la stabilità.
3) Studiare le piccole oscillazioni attorno ad una posizione di equilibrio stabile.
In un piano orizzontale si muovono due sbarrette omogenee di lunghezza
![]() e massa
e massa ![]() di estremi rispettivamente
di estremi rispettivamente ![]() , e
, e ![]() ,
incernierate tra loro in
,
incernierate tra loro in ![]() ma libere di ruotare senza attrito.
Gli estremi
ma libere di ruotare senza attrito.
Gli estremi ![]() e
e ![]() sono obbligati a scorrere senza attrito
lungo un asse fisso
sono obbligati a scorrere senza attrito
lungo un asse fisso ![]() . Su
. Su ![]() agisce una forza
agisce una forza
![]() , su
, su ![]() una forza
una forza
![]() (
(![]() ), ove
), ove
![]() e
e ![]() sono punti dell'asse
sono punti dell'asse ![]() di ascisse rispettivamente
di ascisse rispettivamente
![]() e
e ![]() . Scegliamo come variabili lagrangiane l'ascissa
di
. Scegliamo come variabili lagrangiane l'ascissa
di ![]()
![]() , e l'angolo
, e l'angolo ![]() che
che ![]() forma con l'asse
forma con l'asse ![]() .
.
1) Trovare le equazioni del moto.
2) Trovare le posizioni di equilibirio e discuterne la stabilità.
3) Scrivere le piccole oscillazioni attorno ad una posizione di equilibrio stabile.
4) Trovare se esistono condizioni iniziali per cui il moto sia armonico
con frequenza ![]() non solo per piccole oscillazioni ma anche per
oscillazioni finite.
non solo per piccole oscillazioni ma anche per
oscillazioni finite.
Un disco omogeneo pesante di massa ![]() e
raggio
e
raggio ![]() è vincolato in un piano verticale
a rotolare senza
strisciare su una guida
orizzontale
è vincolato in un piano verticale
a rotolare senza
strisciare su una guida
orizzontale ![]() . Un punto materiale di massa
. Un punto materiale di massa
![]() è vincolato senza attrito al suo bordo. Sul
centro
è vincolato senza attrito al suo bordo. Sul
centro ![]() del disco agisce la forza
del disco agisce la forza
![]() (
(![]() ).
).
1) Determinare gli equilibri e la loro
stabilità, (per ![]() ).
).
2) Scrivere la lagrangiana e le equazioni di
Lagrange studiando, per ![]() , le piccole
oscillazioni attorno alla posizione di
equilibrio stabile. Si calcolino le frequenze
proprie e i modi normali.
, le piccole
oscillazioni attorno alla posizione di
equilibrio stabile. Si calcolino le frequenze
proprie e i modi normali.
3) Per ![]() si determinino 2 integrali primi
del moto.
si determinino 2 integrali primi
del moto.
4) (facoltativo) Per ![]() determinare i moti
tali che la quota del punto materiale rimanga
costante nel tempo.
determinare i moti
tali che la quota del punto materiale rimanga
costante nel tempo.
Un disco omogeneo pesante di massa ![]() e
raggio
e
raggio ![]() è vincolato in un piano verticale
a rotolare senza
strisciare su una guida
orizzontale
è vincolato in un piano verticale
a rotolare senza
strisciare su una guida
orizzontale ![]() . Un punto materiale di massa
. Un punto materiale di massa
![]() è vincolato senza attrito al suo bordo. Sul
centro
è vincolato senza attrito al suo bordo. Sul
centro ![]() del disco agisce la forza
del disco agisce la forza
![]() (
(![]() ).
).
1) Determinare gli equilibri e la loro
stabilità, (per ![]() ).
).
2) Scrivere la lagrangiana e le equazioni di
Lagrange studiando, per ![]() , le piccole
oscillazioni attorno alla posizione di
equilibrio stabile. Si calcolino le frequenze
proprie e i modi normali.
, le piccole
oscillazioni attorno alla posizione di
equilibrio stabile. Si calcolino le frequenze
proprie e i modi normali.
3) Per ![]() si determinino 2 integrali primi
del moto.
si determinino 2 integrali primi
del moto.
4) (facoltativo) Per ![]() determinare i moti
tali che la quota del punto materiale rimanga
costante nel tempo.
determinare i moti
tali che la quota del punto materiale rimanga
costante nel tempo.
Un punto materiale pesante è vincolato senza attrito alla
superficie di rotazione d'asse verticale ![]() , descritta
in coordinate cilindriche dall'equazione
, descritta
in coordinate cilindriche dall'equazione
![]() ,
con
,
con ![]() ,
, ![]() costante positiva minore di
costante positiva minore di ![]() .
.
a) Dimostra che il corrispondente sistema lagrangiano è integrabile.
b) Dimostra che esistono condizioni iniziali tali che il punto si muova mantenendo la quota costante. Descrivi tali moti.
Si consideri la funzione Lagrangiana:
2) Si considerino per il sistema di Lagrangiana ![]() le condizioni iniziali:
le condizioni iniziali:
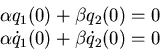 |
(4.2) |
Si studino i corrispondenti moti, individuando in particolare, se esistono, moti a meta asintotica.
Un disco rigido di massa M e raggio ![]() è libero di
scorrere senza attrito su
di un piano orizzontale fisso. Sul bordo del disco puó scorrere, ancora
senza attrito, un punto materiale di massa
è libero di
scorrere senza attrito su
di un piano orizzontale fisso. Sul bordo del disco puó scorrere, ancora
senza attrito, un punto materiale di massa ![]() .
.
Si richiede di determinare il moto del sistema.
In un piano orizzontale sono poste due aste ![]() e
e ![]() di rispettive masse
di rispettive masse ![]() ed
ed ![]() (distribuzione di massa
omogenea) e lunghezze
(distribuzione di massa
omogenea) e lunghezze ![]() ed
ed ![]() . Le aste sono libere di ruotare
attorno ai rispettivi baricentri
. Le aste sono libere di ruotare
attorno ai rispettivi baricentri ![]() e
e ![]() , fissi nel piano,
con
, fissi nel piano,
con
![]() .
.
Sia ![]() un punto appartenente all'asta
un punto appartenente all'asta ![]() , giacente tra
, giacente tra ![]() e
e
![]() ,
, ![]() un punto appartenente all'asta
un punto appartenente all'asta ![]() ,
giacente tra
,
giacente tra
![]() e
e ![]() ,
,
![]() .
Tra i punti
.
Tra i punti ![]() e
e ![]() agisce una molla ideale, di costante elastica
agisce una molla ideale, di costante elastica
![]() . Si richiede:
. Si richiede:
1) scrivere la Lagrangiana del sistema;
2) determinare gli equilibri;
3) discutere la stabilità degli equilibri al variare del parametro
![]() in
in
![]() ;
;
4) considerato il sistema corrispondente a ![]() ,
si discuta il corrispondente sistema lagrangiano, mostrando che è
riconducibile ad un sistema ad un grado di libertà.
,
si discuta il corrispondente sistema lagrangiano, mostrando che è
riconducibile ad un sistema ad un grado di libertà.
Si consideri in un piano orizzontale un punto materiale ![]() , di massa
, di massa ![]() .
Il punto è richiamato, tramite una molla ideale di costante elastica
.
Il punto è richiamato, tramite una molla ideale di costante elastica
![]() , (
, (
![]() , dal punto fisso
, dal punto fisso ![]() . Inoltre, a distanza
. Inoltre, a distanza ![]() da
da ![]() é posto il centro di un cerchio, di raggio
é posto il centro di un cerchio, di raggio ![]() . Il cerchio è fisso. Sul
cerchio è libero di scorrere senza attrito un punto materiale
. Il cerchio è fisso. Sul
cerchio è libero di scorrere senza attrito un punto materiale ![]() di massa
di massa
![]() . I punti
. I punti ![]() e
e ![]() interagiscono tramite una molla ideale di costante
elastica
interagiscono tramite una molla ideale di costante
elastica ![]() , (
, (
![]()
![]() Si scriva la Lagrangiana del sistema e si determinino le
soluzioni stazionarie del corrispondente sistema di Lagrange.
Si scriva la Lagrangiana del sistema e si determinino le
soluzioni stazionarie del corrispondente sistema di Lagrange.
![]() Si discuta la stabilità delle soluzioni di equilibrio trovate al
punto
Si discuta la stabilità delle soluzioni di equilibrio trovate al
punto ![]() , determinando le frequenze delle piccole oscillazioni attorno
alla posizione di equilibrio stabile.
, determinando le frequenze delle piccole oscillazioni attorno
alla posizione di equilibrio stabile.
![]() Si consideri il caso:
Si consideri il caso: ![]() Si dimostri che il sistema
Lagrangiano ha un integrale primo indipendente dall'energia. Si scriva la
funzione di Hamilton del sistema corrispondente al valore nullo di detto
integrale primo, usando come coordinata spaziale indipendente la differenza
delle anomalie angolari di
Si dimostri che il sistema
Lagrangiano ha un integrale primo indipendente dall'energia. Si scriva la
funzione di Hamilton del sistema corrispondente al valore nullo di detto
integrale primo, usando come coordinata spaziale indipendente la differenza
delle anomalie angolari di ![]() e di
e di ![]() .
.
![]() Si consideri il caso limite in cui
Si consideri il caso limite in cui
![]() è
trascurabile rispetto a
è
trascurabile rispetto a ![]() ; si valuti quindi in questa
approssimazione la funzione di Hamilton a partire da quella determinata nel
punto precedente, e si dimostri che il corrispondente sistema Hamiltoniano è
integrabile.
; si valuti quindi in questa
approssimazione la funzione di Hamilton a partire da quella determinata nel
punto precedente, e si dimostri che il corrispondente sistema Hamiltoniano è
integrabile.
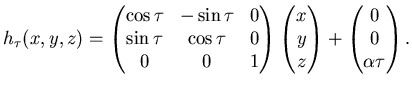 |
(4.3) |
Seconda domanda. Usando la simmetria del sistema si riduca di
uno il numero dei gradi di libertà, considerando quindi una opportuna
Lagrangiana ridotta. Determinare gli equilibri di tale Lagrangiana ridotta e
darne una interpretazione in termini delle coordinate
![]()
Terza domanda. Si studi la stabilità degli equilibri nel caso particolare:
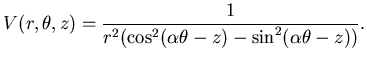 |
(4.4) |
Un punto materiale di massa unitaria è vincolato a muoversi
sulla superficie di rotazione
di equazione
![]() , dove
, dove
![]() .
.
Sul punto agisce una forza costante, di intesità unitaria, diretta
verso la direzione negativa dell'asse ![]() .
.
1) Scrivi la Lagrangiana e l'Hamiltoniana del sistema.
2) Determina gli integrali primi del moto.
3) Determina le condizioni sui dati iniziali per cui il moto esiste per tutti i tempi, per cui si hanno orbite limitate, per cui si hanno orbite illimitate.
4) Considera un'orbita illimitata. È finito
l'angolo
![]() ?
(
?
(![]() è l'angolo che la congiungente tra il punto materiale
e l'asse delle
è l'angolo che la congiungente tra il punto materiale
e l'asse delle ![]() forma con un asse orizzontale fisso).
forma con un asse orizzontale fisso).
5) Risolvi il moto per quadrature mediante la soluzione dell'equazione di Hamilton -Jacobi.
6) Determina la regione dello spazio delle fasi in cui il moto si puó descrivere in variabili azione-angolo e determina le variabili d'azione.
Si consideri, in un piano fisso orizzontale, una guida
![]() , liscia, a forma di arco di parabola, libera di ruotare senza
attrito attorno al suo vertice
, liscia, a forma di arco di parabola, libera di ruotare senza
attrito attorno al suo vertice ![]() , fissato sul piano.
Sia
, fissato sul piano.
Sia ![]() il suo momento di
inerzia rispetto ad
il suo momento di
inerzia rispetto ad ![]() .
In un sistema di coordinate cartesiane
.
In un sistema di coordinate cartesiane
![]() ,
solidale con la guida, essa è rappresentata dall'equazione
,
solidale con la guida, essa è rappresentata dall'equazione
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Un punto materiale ![]() di massa
di massa ![]() , è libero di scorrere
senza attrito sulla guida
, è libero di scorrere
senza attrito sulla guida
![]() . Il punto
. Il punto ![]() é richiamato da
é richiamato da ![]() per il tramite di una molla
elastica di costante
per il tramite di una molla
elastica di costante
![]() .
.
Si denoti con ![]() l'angolo che
la direzione tangente in
l'angolo che
la direzione tangente in ![]() alla guida forma con una direzione fissa
del piano (vedi figura).
alla guida forma con una direzione fissa
del piano (vedi figura).
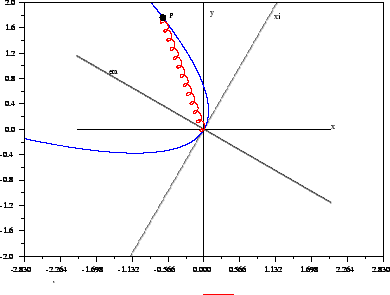
2) Dopo aver riconosciuto l'esistenza di un integrale primo
![]() (ulteriore rispetto all'energia), si analizzino i moti del
sistema unidimensionale che si ottiene fissando il valore di
(ulteriore rispetto all'energia), si analizzino i moti del
sistema unidimensionale che si ottiene fissando il valore di ![]() .
.
3) Si determinino delle condizioni sui dati iniziali per cui il moto del sistema composto dalla guida e dal punto materiale sia periodico.
4) Si scriva l' Hamiltoniana e si discuta l'equazione di Hamilton-Jacobi, con il metodo di separazione delle variabili.
Considera una terna di riferimento inerziale
![]() .
Un disco rigido di massa
.
Un disco rigido di massa ![]() e raggio
e raggio ![]() , e' vincolato ad avere il
centro in
, e' vincolato ad avere il
centro in ![]() . L'asse
. L'asse
![]() , passante per
, passante per ![]() ed ortogonale al disco, è vincolato a muoversi sul piano
ed ortogonale al disco, è vincolato a muoversi sul piano
![]() , ed inoltre
il disco è libero di ruotare intorno a tale asse
, ed inoltre
il disco è libero di ruotare intorno a tale asse
![]() .
.
Sul bordo del disco è fissato un punto materiale ![]() di massa
di massa ![]() , che è richiamato dall'asse
, che è richiamato dall'asse
![]() da una molla di
costante elastica
da una molla di
costante elastica ![]() .
.
Considera il sistema in assenza della forza di gravità.
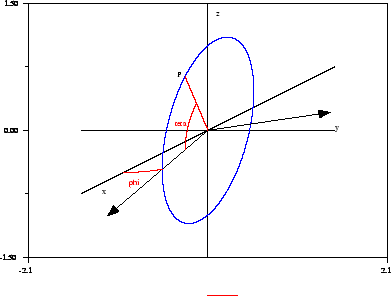
1) Individua i gradi di libertà del sistema e scrivi la Lagrangiana e l'Hamiltoniana.
2) Determina simmetrie ed integrali primi, e riduci lo studio del moto del sistema ad un problema ad un grado di libertà.
3) Studia qualitativamente il moto unidimensionale che hai ottenuto, ed in particolare analizza la stabilità delle soluzioni stazionarie, al variare dei parametri.
4) Risolvi il problema con il metodo di Hamilton-Jacobi e determina la regione dello spazio delle fasi nella quale il moto puó essere descritto in variabili azione-angolo.
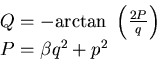 |
(4.5) |
a) Determinare i valori di ![]() per cui
per cui ![]() é canonica;
é canonica;
b) scrivere per tali valori l'espressione esplicita di
![]() .
.
Si consideri la trasformazione
![]()
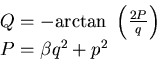 |
(4.6) |
a) Determinare i valori di ![]() per cui
per cui ![]() é canonica;
é canonica;
b) scrivere per tali valori l'espressione esplicita di
![]() .
.
Si consideri la funzione
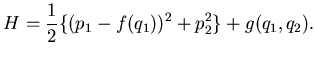 |
(4.7) |
Si dimostri che la trasformazione:
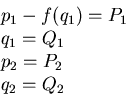 |
(4.8) |
(2). Si consideri quindi la seguente Hamiltoniana:
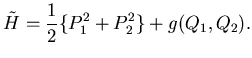 |
(4.9) |
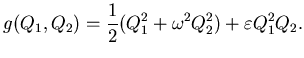 |
(4.10) |
Si dimostri che è possibile introdurre variabili azione-angolo, in modo che in queste nuove variabili l'Hamiltoniana assuma la forma:
| (4.11) |
(3). Si determinino le condizioni su ![]() , talché
con un cambiamento di variabili
simplettico
, talché
con un cambiamento di variabili
simplettico
![]() , la
Hamiltoniana prenda la forma:
, la
Hamiltoniana prenda la forma:
| (4.12) |
Considera l'Hamiltoniana:
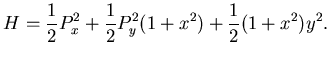 |
(4.13) |
a) Risolvi, per
separazione di variabili, l'equazione di Hamilton Jacobi per ![]() .
.
b) Determina la regione dello spazio delle fasi in cui il moto puó essere descritto in variabili azione-angolo.
c) Calcola esplicitamente l'espressione dell'Hamiltoniana in termini delle variabili d'azione, e le frequenze dei moti multiperiodici.
d) Considera il moto di dato iniziale
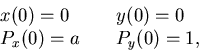 |
(4.14) |
e) Trova il periodo del moto per ![]() .
.
f) Discuti la stabilità della soluzione stazionaria
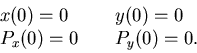 |
(4.15) |
Un'asta omogenea di massa ![]() lunga
lunga
![]() ha un estremo fisso in 0. L'altro
estremo è vincolato senza
attrito su una circonferenza di raggio
ha un estremo fisso in 0. L'altro
estremo è vincolato senza
attrito su una circonferenza di raggio
![]() che giace su
un piano orizzontale e il cui centro è sulla
verticale sotto 0. Un punto materiale pesante
P di massa
che giace su
un piano orizzontale e il cui centro è sulla
verticale sotto 0. Un punto materiale pesante
P di massa ![]() è vincolato senza attriti alla
retta contenente l'asta ed è anche soggetto alla
forza elastica
è vincolato senza attriti alla
retta contenente l'asta ed è anche soggetto alla
forza elastica ![]() ,
, ![]() .
.
1) Scrivere l'hamiltoniana del sistema e individuare due integrali primi del moto.
2) Scrivere le equazioni di Hamilton-Jacobi e portarne alle quadrature la soluzione.
3) Integrare le equazioni di Hamilton-Jacobi
all'ordine zero in ![]() e dare
un'interpretazione fisica del risultato.
e dare
un'interpretazione fisica del risultato.
4) (facoltativo) Valutare la correzione al
primo ordine in ![]() , relativamente al punto 3).
, relativamente al punto 3).