L'esercizio precedente ha una interpretazione termodinamica.
È facile identificare l'energia interna:
![]() . È anche facile identificare il `volume':
sarà
. È anche facile identificare il `volume':
sarà ![]() . La pressione è fisicamente la forza esercitata
sull'unità di superficie che racchiude il mezzo.
D'altra parte in questo caso la superficie è un punto
(
. La pressione è fisicamente la forza esercitata
sull'unità di superficie che racchiude il mezzo.
D'altra parte in questo caso la superficie è un punto
(![]() oppure
oppure ![]() ). Se un punto materiale subisce in un certo tempo
). Se un punto materiale subisce in un certo tempo
![]() una variazione di impulso
una variazione di impulso
![]() , la forza
che è stata esercitata su di esso è
, la forza
che è stata esercitata su di esso è
![]() .
Per un urto n
.
Per un urto n ![]() la variazione di impulso è
la variazione di impulso è ![]() .
Nel nostro caso non c'è variazione di impulso
se non quando la massa tocca
.
Nel nostro caso non c'è variazione di impulso
se non quando la massa tocca ![]() .
Per dare senso alla pressione, si può pensare
di considerare l'impulso scambiato con la parete per un tempo
sufficientemente lungo affinché avvengano molti urti,
ma sufficientemente piccolo affinché la variazione dovuta al moto
della barriera mobile non sia significativa (assunzione
possibile se
.
Per dare senso alla pressione, si può pensare
di considerare l'impulso scambiato con la parete per un tempo
sufficientemente lungo affinché avvengano molti urti,
ma sufficientemente piccolo affinché la variazione dovuta al moto
della barriera mobile non sia significativa (assunzione
possibile se
![]() è molto piccolo).
In altre parole:
è molto piccolo).
In altre parole:
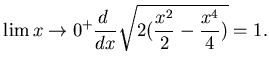
In definitiva, l'interpretazione termodinamica
del moto di una particella tra due pareti perfettamente rigide
a distanza ![]() dà:
dà:
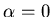
Prova che se ![]() varia molto lentamente,
varia molto lentamente,
Osservazione
Fare la termodinamica di una sola particella è abbastanza privo di senso. Si possono considerare, più correttamente, moltissime particelle tra le pareti, che non urtano tra di loro. Questa situazione può far pensare ad un gas perfetto, per cui la termodinamica ha senso, e la pressione è cinematicamente definita attraverso l'impulso scambiato con le pareti. Tenete presente, però, che un insieme di particelle che non urtano tra loro NON sono un gas perfetto. Infatti manca il meccanismo di termalizzazione tipico, ad esempio, dell'equazione di Boltzmann.