5.7 Altri esempi di invarianti adiabatici

Teorema dell'invarianza adiabatica.

Supponi di avere un moto unidimensionale in cui l'energia totale, oltre che dipendere dalla posizione e dalla velocità, dipenda da un parametro $\lambda$, cioè $E=E(x,\dot x, \lambda)$. Come esempio puoi pensare a $E= \frac 12 \lambda \dot x^2 +V(x)$, dove la massa stessa è il parametro $\lambda$, oppure $E=\frac 12 m\lambda^2\dot \theta^2 -m g\lambda \cos \theta$, dove $\lambda$ ha le dimensioni di una lunghezza.

Supponi, inoltre, che il moto assegnato sia in generle periodico, ed indica con $I(E)$ la misura dell'area, nello spazio delle fasi, della regione racchiusa dall'orbita di energia $E$.

Considera ora il moto con energia totale dipendente dal tempo attraverso $\lambda$: $E=E(x,\dot x, \varepsilon t)$, con $\varepsilon$ piccolo.

Il teorema adiabatico afferma che

$$\vert I(E(t))-I(E(0))\vert\le c \varepsilon ,$$

per $0\le t \le \frac 1\varepsilon$.

In altre parole, per variare l'azione di $\varepsilon$ devo aspettare un tempo di ordine $\frac 1\varepsilon$.

In questo enunciato mancano delle ipotesi importanti. Per l'enunciato preciso e per la dimostrazione vedi, tra gli altri, l'Arnold [1]

Considera un pendolo la cui massa diminuisce lentamente con il tempo. Di quanto varia l'ampiezza delle oscillazioni se la massa si dimezza?

Una massa è appesa ad un filo ed oscilla. Se dimezzo lentamente la lunghezza del filo, come cambia l'ampiezza delle oscillazioni?

Considera il moto unidimensionale di energia totale

$$\frac 12 \dot r^2 + \frac {l^2}{2r^2} - \frac kr.$$

Considera un dato iniziale che compia piccole oscillazioni intorno alla posizione di equilibrio stabile. Se $k$ si dimezza molto lentamente, come cambia il moto?

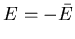
(**) Un satellite in orbita intorno alla Terra descrive un'orbita poco eccentrica. Come cambia l'orbita se il momento della quantità di moto del satellite raddoppia molto lentamente?