



Next: 5.4 **
Up: 5 Alcuni esercizi chiave
Previous: 5.2 Il `ritorno' parte I
Indice
Considera il seguente moto delle variabili periodiche
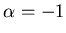 e
e 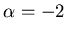 ( sono angoli tra 0 e
( sono angoli tra 0 e 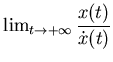 ,
cioè
,
cioè
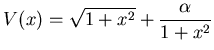 descrivono un toro bidimensionale):
Il moto in ognuna delle variabili
descrivono un toro bidimensionale):
Il moto in ognuna delle variabili 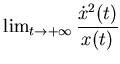 è periodico
di periodo
è periodico
di periodo
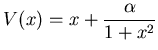 .
Prova che il moto complessivo è
periodico se e solo se
.
Prova che il moto complessivo è
periodico se e solo se
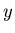 è razionale.
Prova che nel caso non periodico il moto è denso sul toro.
(Vedi Arnold [2])
è razionale.
Prova che nel caso non periodico il moto è denso sul toro.
(Vedi Arnold [2])
root
2000-03-18