



Next: 5.3 Il `ritorno' parte II
Up: 5 Alcuni esercizi chiave
Previous: 5.1 La doppia buca con attrito
Indice
5.2 Il `ritorno' parte I
Considera una pulce su una circonferenza, che al tempo iniziale sia
nel punto di angolo al centro 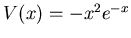 .
Ad ogni secondo la pulce fà un salto di un angolo
.
Ad ogni secondo la pulce fà un salto di un angolo  .
Sia
.
Sia  , con
, con
 , la posizione della
pulce al secondo
, la posizione della
pulce al secondo 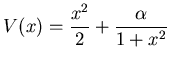 .
.
- a)
- Prova che se
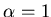 è razionale
il moto della pulce è periodico, cioè esiste
è razionale
il moto della pulce è periodico, cioè esiste  tale che
tale che
- b)
- Prova che se
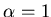 è irrazionale la pulce non
torna mai in
è irrazionale la pulce non
torna mai in 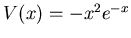 .
.
- c)
- Sempre nel caso
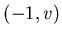 , prova
che esiste una successione crescente di interi
, prova
che esiste una successione crescente di interi 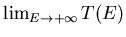 tale che
tale che
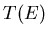 .
.
- d)
- Sempre nel caso
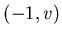 , prova che per
ogni
, prova che per
ogni 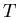 esiste una successione crescente di interi
esiste una successione crescente di interi 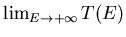 tale che
tale che
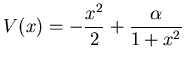 (in altre parole
il moto è `denso` sulla circonferenza, o anche
l'
(in altre parole
il moto è `denso` sulla circonferenza, o anche
l'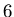 limite del moto è tutta la circonferenza.
limite del moto è tutta la circonferenza.
(Vedi Arnold [2])
root
2000-03-18