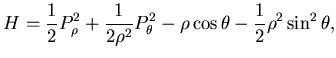Next: 11 Altro
Up: Esercitazioni di Meccanica Razionale
Previous: 9.3 Teoria delle perturbazioni
Indice
10 Ulteriori (Pochi) Esercizi in Formalismo Hamiltoniano
Esercizio 10.1
Due aste omogenee di massa
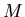
e lunghezza
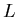
, una
di estremi
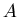
e
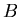
e l'altra di estremi
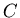
e
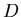
, si muovono
in un piano verticale.
L'estremo
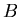
è incernierato, senza attrito,
nel baricentro dell'asta
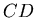
.
Una molla di costante elastica
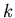
lega
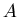
a
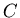
.
1 Determinare i gradi di libertà
2 Scrivere la Lagrangiana
3 Scrivere l'Hamiltoniana
4 Scrivere l'equazione di Hamilton Jacobi
5 Risolvere l'equazione di Hamilton Jacobi
6 Supponendo che inizialmente le aste sono ferme,
con 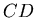 parallela all'asse
delle
parallela all'asse
delle 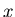 ,,
con l'ascissa di
,,
con l'ascissa di 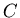 minore dell'ascissa di
minore dell'ascissa di 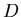 e con
e con 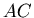 parallela all'asse delle
parallela all'asse delle 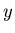 con l'ordinata di
con l'ordinata di 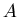 maggiore
dell'ordinata di
maggiore
dell'ordinata di 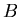 .
Che angolo forma la direzione di
.
Che angolo forma la direzione di 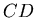 con l'asse orizzontale
quando
con l'asse orizzontale
quando 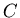 passa per il baricentro di
passa per il baricentro di 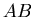 ?
?
Esercizio 10.2
Una circonferenza omogenea, di raggio 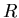 e massa
e massa 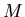 , è vincolata
a muoversi in un piano orizzontale, passando sempre per un punto fisso
, è vincolata
a muoversi in un piano orizzontale, passando sempre per un punto fisso
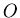 del piano. Un'altra circonferenza di raggio
del piano. Un'altra circonferenza di raggio 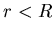 e massa
e massa 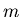 rotola
senza strisciare sul bordo interno della prima.
rotola
senza strisciare sul bordo interno della prima.
1 Scrivere la lagrangiana
2 Scrivere l'hamiltoniana
3 Scrivere l'equazione di Hamilton Jacobi
4 discutere la riconducibilità del moto alle
quadrature e, eventualmente, la regione dello
spazio delle fasi in cui si possono definire le variabili
azione-angolo
Esercizio 10.3
In un piano orizzontale, l'estremo 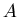 di un'asta omogenea
di massa
di un'asta omogenea
di massa 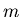 e lunghezza
e lunghezza 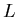 è vincolato a muoversi su di una
guida circolare fissa del piano, di centro
è vincolato a muoversi su di una
guida circolare fissa del piano, di centro 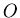 e raggio
e raggio 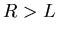 .
L'altro estremo dell'asta è richiamato da
.
L'altro estremo dell'asta è richiamato da 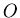 da una molla
di costante elastica
da una molla
di costante elastica 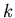 .
.
1 Scrivi la lagrangiana
2 Scrivi l'hamiltoniana
3 Determina la regione nello spazio delle fasi
in cui si possono introdurre le variabili azione-angolo
4 Discuti le posizioni di equilibrio e la loro
stabilità.
5 Prova che esistono moti per cui l'asta rimane
parallela al raggio che passa per 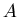 , sia interna che
esterna alla guida. Osserva che sono moti periodici.
, sia interna che
esterna alla guida. Osserva che sono moti periodici.
6 Discuti se le orbire descritte al punto 5
sono stabili, cioè se una piccola perturbazione
dei dati iniziali fa ruotare l'asta in modo che
rimanga per tutti i tempi vicina al raggio 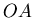 oppure no.
oppure no.
7 Trova un'altra famiglia di soluzioni periodiche, oltre
a quelle descritte nel punto 5.
Esercizio 10.4
Sia
e sia, al tempo 0
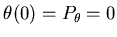
e
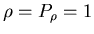
.
Sia
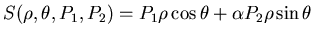
,
con
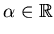
una funzione generatrice, con
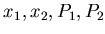
nuove coordinate ed impulsi.
Determina i valori di
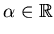
tali
che l'hamiltoniana nelle nuove variabili sia
integrabile.
Utilizza tale trasformazione per
determinare il valore di
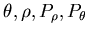 al tempo
al tempo
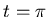 .
.




Next: 11 Altro
Up: Esercitazioni di Meccanica Razionale
Previous: 9.3 Teoria delle perturbazioni
Indice
root
2001-04-02
![]() parallela all'asse
delle
parallela all'asse
delle ![]() ,,
con l'ascissa di
,,
con l'ascissa di ![]() minore dell'ascissa di
minore dell'ascissa di ![]() e con
e con ![]() parallela all'asse delle
parallela all'asse delle ![]() con l'ordinata di
con l'ordinata di ![]() maggiore
dell'ordinata di
maggiore
dell'ordinata di ![]() .
Che angolo forma la direzione di
.
Che angolo forma la direzione di ![]() con l'asse orizzontale
quando
con l'asse orizzontale
quando ![]() passa per il baricentro di
passa per il baricentro di ![]() ?
?