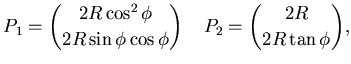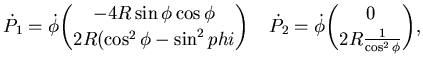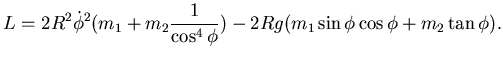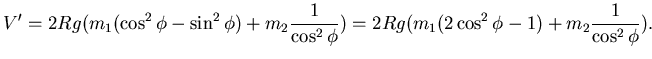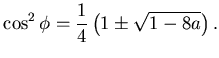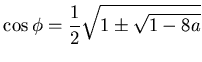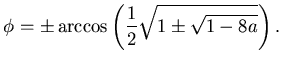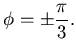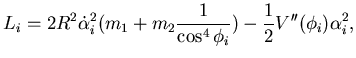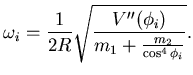Next: Bibliografia
Up: Esercitazioni di Meccanica Razionale
Previous: 10 Ulteriori (Pochi) Esercizi
Indice
11 Altro
Soluzione
Il problema è evidentemente ad un solo grado si libertà.
Scelgo come variabile l'angolo 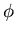 che la direzione
che la direzione
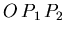 forma con l'asse delle
forma con l'asse delle 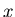 .
Per i vincoli presenti,
.
Per i vincoli presenti,
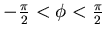 .
Con un po' di trigonometria elementare si ottiene:
.
Con un po' di trigonometria elementare si ottiene:
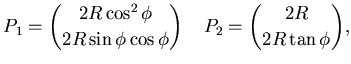 |
(11.1) |
quindi:
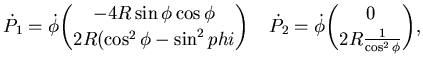 |
(11.2) |
L'energia potenziale dovuta alla forza di gravità è
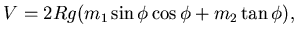 |
(11.3) |
dove 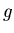 è l'accelerazione di gravità.
è l'accelerazione di gravità.
Quadrando e sommando i termini cinetici si ottiene la Lagrangiana:
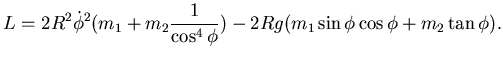 |
(11.4) |
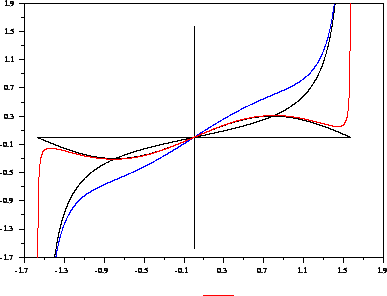
Per analizzare le posizioni di equilibrio, prima del calcolo delle
derivate, tento un grafico qualitativo dell'energia potenziale 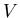 ,
ricordandomi che
,
ricordandomi che
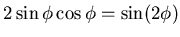 .
.
In nero ho disegnato il seno di 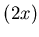 e la tangente di
e la tangente di 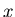 ,
nell'intervallo
,
nell'intervallo
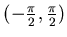 .
La curva blu è la somma, con coefficienti davanti al seno e
alla tangente, dello stesso ordine,
la curva rossa l'ho ottenuta con un coefficiente davanti alla tangente
molto piu' piccolo del coefficiente davanti al seno.
I due coefficienti sono esattamente le masse. Dunque deve
esistere un valore critico
.
La curva blu è la somma, con coefficienti davanti al seno e
alla tangente, dello stesso ordine,
la curva rossa l'ho ottenuta con un coefficiente davanti alla tangente
molto piu' piccolo del coefficiente davanti al seno.
I due coefficienti sono esattamente le masse. Dunque deve
esistere un valore critico 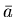 del parametro
del parametro
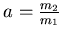 tale che:
tale che:
- per
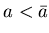 ci sono quattro posizioni di
equilibrio;
nell'ordine crescente di
ci sono quattro posizioni di
equilibrio;
nell'ordine crescente di 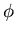 : instabile stabile instabile stabile;
: instabile stabile instabile stabile;
- per
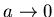 le posizioni estreme tendono a
le posizioni estreme tendono a  ,
le altre tendono alle posizioni di equilibrio per il potenziale
,
le altre tendono alle posizioni di equilibrio per il potenziale
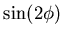 , che sono evidentemente
, che sono evidentemente
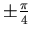 ;
;
- per
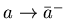 le due posizioni di equilibrio a sinistra andranno
a coincidere, cosí come le due a destra (vviamente saranno
tutte instabili);
le due posizioni di equilibrio a sinistra andranno
a coincidere, cosí come le due a destra (vviamente saranno
tutte instabili);
- per
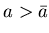 non ci sono posizioni di equilibrio: qualunque sia
il dato iniziale
non ci sono posizioni di equilibrio: qualunque sia
il dato iniziale
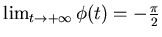 ,
cioè l'ordinata di
,
cioè l'ordinata di 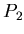 va a
va a 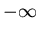 e
e  .
.
Procedendo esplicitamente:
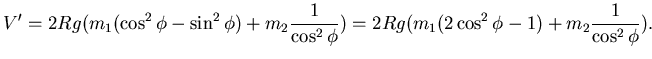 |
(11.5) |
Le posizioni di equilibrio le ottengo annullando 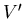 ,
risolvendo, cioè:
,
risolvendo, cioè:
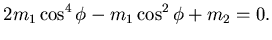 |
(11.6) |
Ottengo
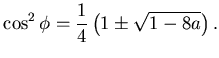 |
(11.7) |
Dunque il valore critico del parametro è
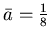 .
Per
.
Per 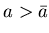 non ci sono soluzioni.
Per
non ci sono soluzioni.
Per 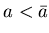 si ha
si ha 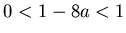 , dunque
, dunque
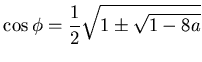 |
(11.8) |
(scarto i valori negativi perchè
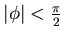 ).
In definitiva ho le quattro posizioni di equilibrio che mi aspettavo:
).
In definitiva ho le quattro posizioni di equilibrio che mi aspettavo:
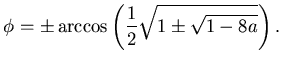 |
(11.9) |
Per 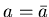 esse coincidono a due a due, nei punti
esse coincidono a due a due, nei punti
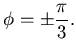 |
(11.10) |
L' analisi della stabilità è facilmente ottenibile dal
grafico.
Per 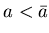 esistono due posizioni di equilibrio stabile:
esistono due posizioni di equilibrio stabile:
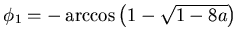 e
e
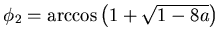 .
Il modo più pulito per determinare la frequenza delle piccole
oscillazioni è quello di scrivere la lagrangiana delle
piccole oscillazioni. Per fare ciò bisogna calcolare
la derivata seconda dell'energia potenziale.
La indico con
.
Il modo più pulito per determinare la frequenza delle piccole
oscillazioni è quello di scrivere la lagrangiana delle
piccole oscillazioni. Per fare ciò bisogna calcolare
la derivata seconda dell'energia potenziale.
La indico con 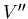 .
Detto
.
Detto 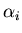 lo scostamento dall'equilibrio
lo scostamento dall'equilibrio 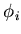 (
(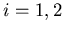 ),
le lagrangiane delle piccole oscillazioni sono:
),
le lagrangiane delle piccole oscillazioni sono:
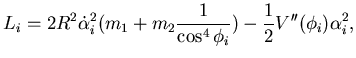 |
(11.11) |
quindi le frequenze delle piccole oscillazioni intorno ai due
equilibri stabili sono:
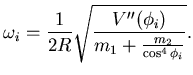 |
(11.12) |
(Notare che, svolti i conti, esse dipendono solo dal rapporto tra
le masse 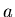 ).
).




Next: Bibliografia
Up: Esercitazioni di Meccanica Razionale
Previous: 10 Ulteriori (Pochi) Esercizi
Indice
root
2001-04-02
![]() di origine
di origine ![]() ,
considerate il sistema materiale
formato da due punti
,
considerate il sistema materiale
formato da due punti ![]() ,
di massa
,
di massa
![]() , rispettivamente; un vincolo liscio obbliga
, rispettivamente; un vincolo liscio obbliga
![]() ad essere allineati.
Inoltre il punto
ad essere allineati.
Inoltre il punto ![]() è vincolato a muoversi lungo la
circonferenza di centro
è vincolato a muoversi lungo la
circonferenza di centro ![]() e raggio
e raggio ![]() , ed il punto
, ed il punto ![]() è
vincolato a muoversi lungo la retta
è
vincolato a muoversi lungo la retta ![]() .
.
![]() si possono avere
posizioni di equilibrio;
si possono avere
posizioni di equilibrio;