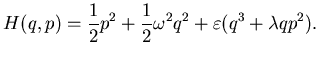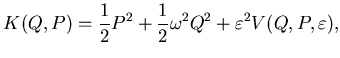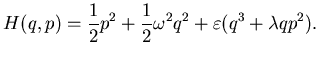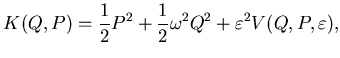9.3 Teoria delle perturbazioni

Esercizio 9.12   Si consideri l'Hamiltoniana

$$H(q,p)= \frac 12 p^2 + \frac 12 \omega^2 q^2 + \varepsilon ( q^3 + \lambda qp^2).$$

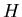
Si trovi una trasformazione canonica polinomiale, che trasforma $H$ in una Hamiltoniana della forma:

$$K(Q,P)=\frac 12 P^2 + \frac 12 \omega^2 Q^2 + \varepsilon ^2 V(Q,P,\varepsilon ),$$

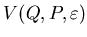
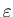
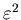
con $V(Q,P,\varepsilon )$ limitato in $\varepsilon$. Si utilizzi tale trasformazione per scrivere la soluzione generale delle equazioni del moto a meno di termini di oridine $\varepsilon ^2$.