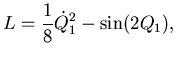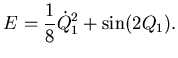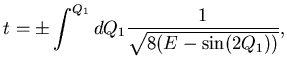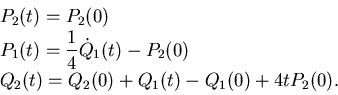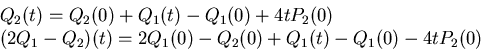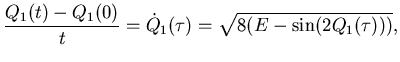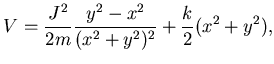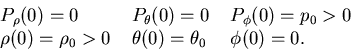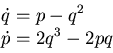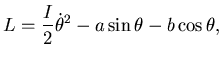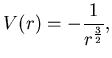Next: 9.3 Teoria delle perturbazioni
Up: 9 Altri Esercizi in
Previous: 9.1 Trasformazioni Canoniche
Indice
Esercizio 9.5 (by Negrini, 2000)
Si consideri l'hamiltoniana
e si consideri la funzione generatrice
a) Si determini la trasformazione canonica individuata da 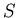 ,
nella regione
,
nella regione
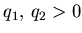 .
.
b) Si determini la nuova Hamiltoniana.
c) Si determinino le soluzioni delle equazioni del moto
per la nuova Hamiltoniana.
d) Le soluzioni ottenute permettono di trovare le
soluzioni delle equazioni del moto nelle vecchie variabili?
Soluzione.
a) La funzione generatrice dipende dalle vecchie coordiante e
dai nuovi impulsi. Pertanto la traformazione canonica
è implicitamente definita da:
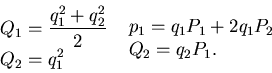 |
(9.5) |
La trasformazione canonica è dunque:
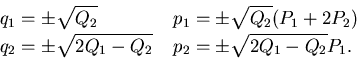 |
(9.6) |
Nella regione
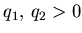 il segno da scegliere è
il segno da scegliere è 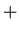 .
.
b) Sostituendo nell'espressione di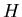 si ottiene l'hamiltoniana nelle
nuove variabili:
si ottiene l'hamiltoniana nelle
nuove variabili:
c)
La variabile 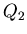 è ciclica, dunque
è ciclica, dunque 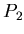 si conserva, e
si conserva, e 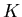 si conserva.
Un modo per ottenere la quadratura del moto è di scrivere la
lagrangiana unidimensionale per la variabile
si conserva.
Un modo per ottenere la quadratura del moto è di scrivere la
lagrangiana unidimensionale per la variabile 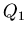 , pensando
, pensando 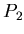 come un parametro fissato (un altro
è la soluzione dell'equazione di Hamilton-Jacobi, per separazione
di variabili, o l'ispezione diretta delle equazioni del moto).
Si ottiene
come un parametro fissato (un altro
è la soluzione dell'equazione di Hamilton-Jacobi, per separazione
di variabili, o l'ispezione diretta delle equazioni del moto).
Si ottiene
dove
La lagrangiana è:
In questa lagrangiana il termine 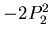 è costante, e posso
eliminarlo,
inoltre il termine
è costante, e posso
eliminarlo,
inoltre il termine
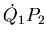 è una derivata totale
ripetto al tempo (
è una derivata totale
ripetto al tempo (
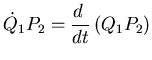 ),
quindi non influisce sulle equazioni del moto, e posso elimare
anch'esso.
In definitiva la Lagrangiana che descrive il moto è
che ha come energia totale
L'analisi qualitativa di questo moto è assolutamente standard.
),
quindi non influisce sulle equazioni del moto, e posso elimare
anch'esso.
In definitiva la Lagrangiana che descrive il moto è
che ha come energia totale
L'analisi qualitativa di questo moto è assolutamente standard.
Il moto di 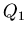 è descritto da:
è descritto da:
la determinazione del moto nelle altre variabili
è determinato integrando le equazioni di Hamilton:
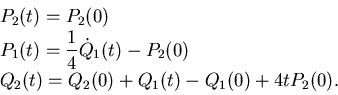 |
(9.7) |
d)
La trasformazione effettuata è valida solo fino a che
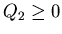 e
e
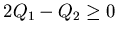 .
Quindi posso ottenere le soluzioni nelle vecchie
variabili solo fino a quando
.
Quindi posso ottenere le soluzioni nelle vecchie
variabili solo fino a quando
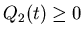 e
e
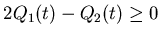 .
Dalle soluzioni delle equazioni di Hamilton si ottiene:
.
Dalle soluzioni delle equazioni di Hamilton si ottiene:
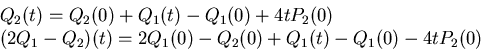 |
(9.8) |
Ne segue che se
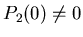 , e il moto in
, e il moto in 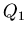 è limitato,
il moto raggiunge o la frontiera
è limitato,
il moto raggiunge o la frontiera 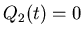 o
la frontiera
o
la frontiera
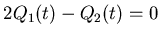 .
Infatti, o
.
Infatti, o
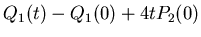 o
o
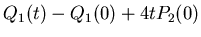 tende a meno infinito.
tende a meno infinito.
Quindi la soluzione trovata non può essere estesa per tutti
i tempi nelle vecchie variabili.
Per ottenere la soluzioni per tutti i tempi
bosogna considerare la trasfrmazione canonica
nelle altre regioni dello spazio delle fasi.
Esistono, però, dati iniziali per cui si ottiene
globalemente il moto nelle vecchie variabili.
Sia ad esempio 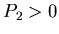 e consideriamo i moti illimitati in
e consideriamo i moti illimitati in 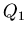 ,
con
,
con
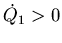 (che corrispondono a
(che corrispondono a 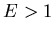 ).
Allora,
se
).
Allora,
se
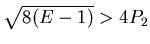 , le condizioni per l'invertibilità sono
sempre soddisfatte, infatti:
, le condizioni per l'invertibilità sono
sempre soddisfatte, infatti:
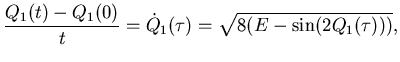
per un opportuno tempo intermedio 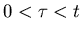 .
Dunque:
.
Dunque:
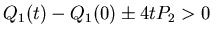 .
.
Esercizio 9.6 ((III Esonero 26/5/97, seconda parte)
Un'asta omogenea di massa 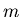 e lunghezza
e lunghezza 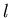 è vincolata
a muoversi su di un piano orizzontale
è vincolata
a muoversi su di un piano orizzontale
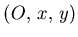 .
Sul suo punto medio
.
Sul suo punto medio 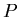 è applicata una forza di energia potenziale
è applicata una forza di energia potenziale
dove
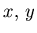
sono le coordinate del punto
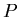
, e
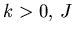
paramteri
fissati.
Usa come variabili lagrangiane la distanza 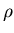 di
di 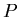 dall'origine
dall'origine
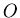 ,
l'angolo
,
l'angolo 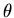 che
che 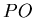 forma con l'asse delle
forma con l'asse delle 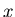 , e l'angolo
, e l'angolo 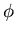 che l'asta forma con l'asse delle
che l'asta forma con l'asse delle 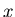 .
.
a)
Scrivi la Lagrangiana e l'Hamiltoniana;
b) risolvi l'equazione di Hamilton-Jacobi per separazione
di variabili;
c) considera il dato iniziale
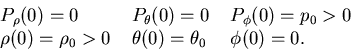 |
(9.9) |
Per quali valori di
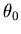
il moto è multiperiodico (
cioè è nella regione dello spazio delle fasi in cui il moto può
essere descritto in variabili azione-angolo)?
d) Sia ora
 . Trova un valore di
. Trova un valore di 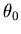 per
cui il moto è periodico.
per
cui il moto è periodico.
Esercizio 9.7 (III Esonero 1/6/95 (Marchioro) seconda parte)
In un piano verticale è posto un disco omogeneo di centro 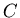 , masa
, masa
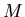 e raggio
e raggio 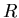 , che rotola senza strisciare lungo un asse orizzontale
, che rotola senza strisciare lungo un asse orizzontale
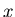 . In tale piano è posta un'asta omogenea pesante di massa
. In tale piano è posta un'asta omogenea pesante di massa 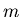 e lunghezza
e lunghezza 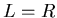 ed i cui estremi
ed i cui estremi 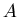 e
e 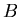 sono obbligati a scorrere
senza attrito lungo una guida liscia solidale alla circonferenza
del disco.
sono obbligati a scorrere
senza attrito lungo una guida liscia solidale alla circonferenza
del disco.
Scegliamo come variabili Lagrangiane l'ascisa 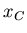 del centro del
disco e l'angolo
del centro del
disco e l'angolo 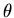 che
che 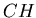 forma con la verticale
discendente, ove
forma con la verticale
discendente, ove 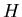 è il punto di mezzo dell'asta
è il punto di mezzo dell'asta 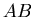 .
.
a) Scrivere le equazioni del moto con il metodo di Lagrange.
b) Trovare due integrali primi e, tramite questi, considerando
le seguenti condizioni inizilali:
trovare i valori di
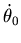
per cui l'asta compie una rotazione
completa.
c) Scrivere prima l'Hamiltoniana e poi
l'equazione di Hamilton-Jacobi.
d) (aggiunto) Risolvere per separazione di variabili l'equazione
di Hamilton-Jacobi. Esiste una regione nello spazio delle fasi
in cui il motot può essere descritto in variabile azione-angolo?
Esercizio 9.8 (Esonero 19/5/92 (recupero), seconda parte)
Data la Lagrangiana
a) Scrivere la corrispondente Hamiltoniana e le equazioni di
Hamilton.
b) Scirvere l'equazione di Hamilton-Jacobi relativa a tale
Hamiltoniana e riportare il moto del sistema alle quadrature.
c) Scrivere l'energia meccanica totale corrispondente alla
Lagrangiana 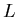 . Utilizzando la conservazione dell'energia,
riportare il sistema alle quadrature. Confrontare il risultato
con quanto ottenuto mediante l'equazione di Hamilton-Jacobi.
. Utilizzando la conservazione dell'energia,
riportare il sistema alle quadrature. Confrontare il risultato
con quanto ottenuto mediante l'equazione di Hamilton-Jacobi.
Esercizio 9.9 (Compito 12/10/94, seconda parte)
Si consideri il sistema di equazioni differenziali
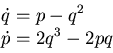 |
(9.10) |
a) Si riconosca che il sistema è hamiltoniano.
b) Si risolva il sistema usando il metodo di Hamilton-Jacobi.
Esercizio 9.10 (Compito 23/9/91)
Un corpo rigido è formato da un semidisco omogeneo di massa 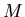 e raggio
e raggio
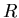 e da un'asta di massa
e da un'asta di massa 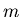 e lunghezza
e lunghezza 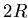 .
Esso è vicolato da una cerniera a ruotare attorno a
.
Esso è vicolato da una cerniera a ruotare attorno a 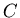 in un piano
verticale, e sia
in un piano
verticale, e sia 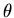 l'angolo che l'asta forma con l'asse
(vedi figura).
l'angolo che l'asta forma con l'asse
(vedi figura).
a) Scirvere la Lagrangiana e mostrare che essa assume la forma
e scrivere le espressioni di
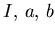
in funzione dei
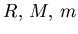
.
b) Determinata l'Hamiltoniana, scrivere l'equazione di Hamilton-Jacobi
e risolvere il problema della dinamica del corpo riportando tale
equazione alle quadrature.
c) Dire sotto quali condizioni la posizione 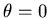 è di equilibrio.
AQl di fuori di tali condizioni studiare il moto del corpo con
condizioni iniziali
è di equilibrio.
AQl di fuori di tali condizioni studiare il moto del corpo con
condizioni iniziali
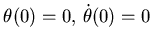 .
Specificare se la rotazione avviene inizialemente in senso orario o
antiorario, se esiste un tempo
.
Specificare se la rotazione avviene inizialemente in senso orario o
antiorario, se esiste un tempo 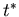 in cui l'asta raggiunge una posizione
verticale ed in tal caso determinare l'espressione di tale tempo
in cui l'asta raggiunge una posizione
verticale ed in tal caso determinare l'espressione di tale tempo 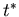 .
.
Esercizio 9.11 (Compito 5/6/90, prima parte)
Una particella puntiforme di massa  si muove nel piano
sotto l'azione di una forza conservativa di energia potenziale
si muove nel piano
sotto l'azione di una forza conservativa di energia potenziale
esendo
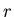
la distanza dall'origine.
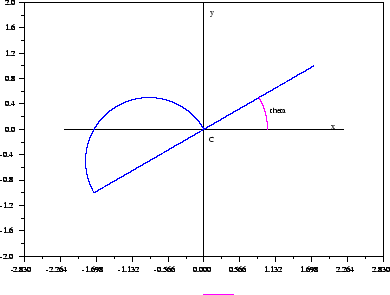
Si supponga che, all'istante 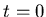 , indicando con
, indicando con 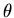 l'angolo polare rispetto all'origine:
l'angolo polare rispetto all'origine:
Si chiede di dire per quali valori di
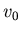
il moto è quasi periodico.




Next: 9.3 Teoria delle perturbazioni
Up: 9 Altri Esercizi in
Previous: 9.1 Trasformazioni Canoniche
Indice
root
2001-04-02
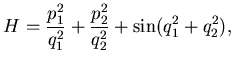
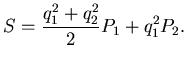
![]() ,
nella regione
,
nella regione
![]() .
.
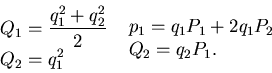
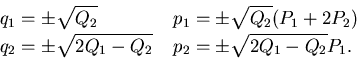
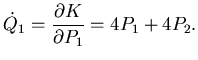
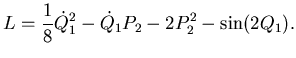
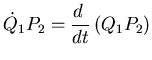 ),
quindi non influisce sulle equazioni del moto, e posso elimare
anch'esso.
In definitiva la Lagrangiana che descrive il moto è
),
quindi non influisce sulle equazioni del moto, e posso elimare
anch'esso.
In definitiva la Lagrangiana che descrive il moto è