Considera la famiglia di trasformazioni da
![]() in
in
![]() :
:
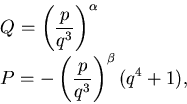 |
(9.1) |
con
a) Trova i valori di ![]() e
e ![]() per i quali la
trasformazione è canonica.
per i quali la
trasformazione è canonica.
b) Determina la funzione generatrice del tipo ![]() della
trasformazione.
della
trasformazione.
Considera la famiglia di trasformazioni da
![]() in
in
![]() :
:
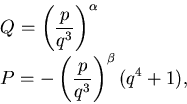 |
(9.1) |
a) Trova i valori di ![]() e
e ![]() per i quali la
trasformazione è canonica.
per i quali la
trasformazione è canonica.
b) Determina la funzione generatrice del tipo ![]() della
trasformazione.
della
trasformazione.
Si consideri la trasformazione
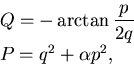 |
(9.2) |
Trovare per quali valori di
![]() la seguente trasformazione
è canonica:
la seguente trasformazione
è canonica:
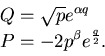 |
(9.3) |
Data la seguente trasformazione:
![]()
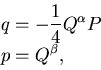 |
(9.4) |