 |
Quelli che trovate qui sono esercizi in forma di test a risposta multipla, raccolti tra quelli di esame.
Al contrario di quello che accade in genere per i test, qui non si tratta di sapere o no la riposta, o di riconoscere rapidamente quella giusta da quelle sbagliate. Quasi tutti gli esercizi in questa raccolta vanno risolti con carta e penna, fino a trovarne la risposta. Solo successivamente la risposta va cercata tra quelle disponibili. Tenete inoltre presente che mentre preparo gli esercizi tento di immaginare gli errori che potete commettere, e inserisco le corrispondenti risposte errate tra quelle possibili.
Segnalatemi gli inevitabili errori che troverete. Buon lavoro.
Roma, 14 ottobre 2008 Dario Benedetto
Docente: Dario Benedetto, tel. 06 49914972 benedetto@mat.uniroma1.it
Materiale e informazioni si trovano alla pagina http://brazil.mat.uniroma1.it/dario/biotec
Orario di ricevimento: mercoledì ore 15.00-17.00, studi di Matematica, edificio Ex-Falegnameria (vedi la piantina, punto D).
Pianta della Città Universitaria con Dipartimento e Studi di Matematica (Ex-Falegnameria)
 |
Il corso è costituito da due moduli:
primo modulo (I semestre) Matematica: 5 crediti
secondo modulo (II semestre) Matematica e uso dei calcolatori: 3 crediti di pratica in laboratorio
L’esame è unico per i due moduli, la prima sessione è in giugno-luglio del 2009 (due appelli). Nel periodo di interruzione gennaio-febbraio 2009 si terrà un esonero scritto che, se superato, esonera dal sostenere la parte di esame relativa al I modulo.
Per il modulo di Matematica l’esame è sostanzialemente scritto (test a risposta multipla); per la parte di laboratorio (modulo di Matematica e uso dei calcolatori) l’esame è sostanzialemente pratico.
La frequenza è in generale obbligatoria per tutti i corsi del corso di laurea. In ogni caso è fortemente consigliata, nel senso che, per esperienza, chi non frequenta ha più difficoltà a superare l’esame, compresi gli studenti dei licei scientifici che ritengono di possedere già le conoscenze degli argomenti del corso.
Sono previste prove in itinere per il I modulo.
Testi consigliati per il I modulo
La presentazione degli argomenti è fatta attraverso esempi (biologici, fisici, e più in generale applicativi), e ha come come scopo quello di rendere lo studente capace di usare concretamente la matematica nei contesti in cui la incontrerà nello studio e nel lavoro.
Non presuppone nessuna conoscenza specialistica precedente, se non la geometria e l’algebra elementari. Ciò nonostante nel testo sono trattati anche argomenti avanzati,
Programma del corso di Matematica (I modulo)
Argomenti delle lezioni (circa 2 ore per lezione):
| Algebra lineare | |
| 1 | vettori, descrizione fisica e geometrica, moltiplicazione per uno scalare, |
| somma e regola del parallelogramma; lunghezza di un vettore, versori, | |
| richiami di trigonometria, prodotto scalare e vettoriale, proiezioni. | |
| 2 | matrici, somma e prodotto riga-colonna; risolubilità e risoluzione dei sistemi lineari, |
| interpretazione geometrica. | |
| Funzioni elementari e non | |
| 3 | definizione di funzione, leggi lineari, coefficiente angolare; retta per due punti; |
| leggi lineari a tratti, crescenza e decrescenza, massimi, minimi; | |
| modulo; disequazioni, parabole. | |
| 4 | potenze, esponenziale e leggi esponenziali, algebra degli esponenziali; |
| logaritmi e algebra dei logaritmi | |
| 5 | sistemi dinamici discreti |
| Calcolo differenziale | |
| 6 | limiti e ordini di infiniti e infinitesimi. |
| 7 | derivata, significato analitico, geometrico, fisico; differenziale; |
| derivata delle funzioni elementari, della somma, del prodotto, del reciproco. | |
| 8 | derivata delle funzioni di funzione, derivata della funzione inversa, studio di funzione. |
| 9 | funzioni di piú variabili, derivate direzionali, gradiente, differenziale. |
| Calcolo integrale | |
| 10 | primitive, calcolo delle aree e dei volumi, integrale definito |
| teorema fondamentale del calcolo; densità | |
| 11 | regole di integrazione, integrali in piú variabili |
| 12 | integrali di linea, differenziali esatti, applicazioni |
| Probabilità | |
| 13 | probabilità discreta, eventi, media, varianza, osservabili. |
| 14 | probabilità condizionate, indipendenza; formula di Bayes e test diagnostici. |
| 15 | prove ripetute; distribuzione binomiale, multinomiale; |
| applicazioni alla genetica di popolazione. | |
| 16 | probabilità continua, densità e funzione di distribuzione, distribuzioni di uso comune. |
1) Il vettore v = (k, log k,k - 2) è perpendicolare a w = (0, 0, 1) ed ha modulo |v| = 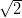 per
per
|
(A) k = 2 (B) k = 1 (C) nessun valore di k |
—————————————————————————
2) Sia v = (v1, v2, v3) un vettore. La sua lunghezza è
(A) |v1 | + |v2| + |v3|
(B) 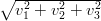
(C) 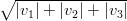
(D) v1 + v2 + v3
(E) 3
—————————————————————————
3) Per quali valori di k i vettori v = 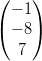 e w =
e w = 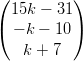 sono ortogonali?
sono ortogonali?
|
(A) per nessun valore di k (B) per k = 0 (C) per k = 2 (D) per k = -2 |
—————————————————————————
4) La lunghezza del vettore (-1 2 3) è
|
(A) (B) (C) -4 (D) 4 (E) 6 (F) 3 |
—————————————————————————
5) La lunghezza del vettore 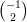 è
è
|
(A) -1 (B) 2 (C) 3 (D) 1 (E) (F) |
—————————————————————————
6) Sia v1 = (1, - 2, 2) e v2 = (4, - 4, - 2); sia l la lunghezza del vettore v1. Il vettore v2 è lungo
|
(A) -4l (B) 4l (C) 2l (D) -2l |
—————————————————————————
7) Siano v = 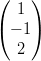 e w =
e w = 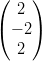 . I vettori orgonali ad entrambi e lunghi 2 sono
. I vettori orgonali ad entrambi e lunghi 2 sono
|
(A) nessuno (B) due (C) infiniti |
—————————————————————————
8) La lunghezza della proiezione di 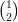 sulla direzione del vettore
sulla direzione del vettore 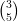 è
è
(A) 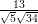
(B) 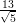
(C) 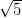 +
+ 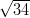
(D) 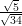
(E) 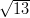
(F) 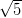
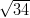
(G) 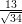
—————————————————————————
9) Siano v = 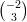 , w =
, w = 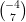 . Quanti sono i vettori x che soddisfano contemporaneamente x ⋅ v = 4 e
x ⋅ w = 9?
. Quanti sono i vettori x che soddisfano contemporaneamente x ⋅ v = 4 e
x ⋅ w = 9?
|
(A) uno (B) infiniti (C) due (D) nessuno |
—————————————————————————
10) Per quale valore di a i vettori v = 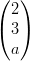 e w =
e w = 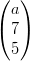 sono ortogonali?
sono ortogonali?
|
(A) -3 (B) 5 (C) -7 (D) 2 (E) 3 (F) 7 (G) -5 (H) -2 |
—————————————————————————
11) Siano: v = 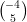 e w =
e w = 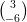 . Il vettore v è più lungo del vettore w?
. Il vettore v è più lungo del vettore w?
|
(A) no (B) si |
—————————————————————————
12) Sia v = (-3, 4, 8), e w = (-4a, - 3a, 9), dove a è un parametro reale. Il prodotto scalare v ⋅ w è nullo per
|
(A) tutti i valori di a (B) nessun valore di a (C) un solo valore di a |
—————————————————————————
13) Siano e1 = 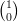 , e2 =
, e2 = 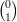 , v =
, v = 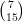 . La lunghezza della proiezione di e1 su v è maggiore della
lunghezza della proiezione di e2 su v?
. La lunghezza della proiezione di e1 su v è maggiore della
lunghezza della proiezione di e2 su v?
|
(A) si (B) no |
—————————————————————————
14) I vettori v = (-4r, - 3r, 9), e w = (-3, 4, 8), dove r è un parametro reale, sono ortogonali per
|
(A) un solo valore di r (B) nessun valore di r (C) tutti i valori di r |
—————————————————————————
|
1 C 2 B 3 A 4 B 5 E 6 C 7 B 8 G 9 A 10 A 11 A 12 B 13 B 14 B |
1) Date le matrici A = 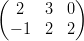 e B =
e B = 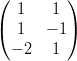
(A) esiste il prodotto AB
(B) esiste il prodotto BA
(C) esistono i prodotti AB e BA
(D) non esiste né il prodotto AB né il prodotto BA
—————————————————————————
2) Date le matrici A = 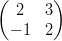 e B =
e B = 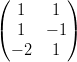
(A) esiste il prodotto BA
(B) esiste il prodotto AB
(C) esistono i prodotti AB e BA
(D) non esiste né il prodotto AB né il prodotto BA
—————————————————————————
3) Date le matrici A = 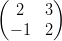 e B =
e B = 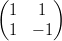
(A) esiste il prodotto AB
(B) esistono i prodotti AB e BA
(C) esiste il prodotto BA
(D) non esiste né il prodotto AB né il prodotto BA
—————————————————————————
4) Date le matrici A = 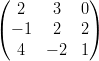 e B =
e B = 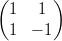
(A) non esiste né il prodotto AB né il prodotto BA
(B) esistono i prodotti AB e BA
(C) esiste il prodotto BA
(D) esiste il prodotto AB
—————————————————————————
5) Date le matrici A = 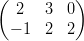 e B =
e B = 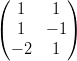
(A) esiste il prodotto BA
(B) esiste il prodotto AB
(C) non esiste né il prodotto AB né il prodotto BA
(D) esistono i prodotti AB e BA
—————————————————————————
6) Sia A una matrice di 2 righe e 3 colonne e B una matrice di 3 righe e 2 colonne. Esiste il prodotto AB?
|
(A) si (B) no |
—————————————————————————
7) Date due matrici A e B, entrambe di due righe e due colonne e un numero reale a. E’ vero che A(aB) = aAB?
|
(A) si (B) no |
—————————————————————————
8) Se A è una matrice 2 × 3, e a un numero reale, aA è
|
(A) un numero reale (B) non esiste (C) un vettore 3 × 1 (D) una matrice 2 × 3 (E) una matrice 3 × 2 (F) un vettore 1 × 3 |
—————————————————————————
9) Sia A una matrice quadrata 2 × 2, sia v un vettore riga a due componenti, e w un vettore colonna a due componenti. Quale tra i seguenti prodotti riga-colonna esiste?
|
(A) wA (B) wAv (C) Av (D) wvA |
—————————————————————————
10) Se A = 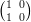 e B =
e B = 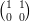
(A) i prodotti AB e BA esistono e AB = BA
(B) il prodotto BA esiste, il prodotto AB non esiste
(C) il prodotto AB esiste, il prodotto BA non esiste
(D) i prodotti AB e BA non esistono
(E) i prodotti AB e BA esistono e AB≠BA
—————————————————————————
11) Siano A = 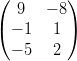 e B =
e B = 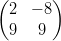 ;
;
(A) il prodotto AB esiste, il prodotto BA non esiste
(B) il prodotto BA esiste, il prodotto AB non esiste
—————————————————————————
12) La seguente tabella contiene, in unità di misura fittizie, la produzione media di ossidi di carbonio CO, di idrocarburi HC, di ossidi di azoto NOx, per autoveicoli a benzina catalizzati K, non catalizzati NK, a gpl GPL, diesel D.
| K | NK | GPL | D | |
| CO | 0.1 | 2 | 2 | 0.01 |
| HC | 20 | 100 | 500 | 0.1 |
| NOx | 20 | 200 | 100 | 100 |
Dieci anni fa 50% degli autoveicoli erano di tipo K, 10% di tipo NK, 5% di tipo GPL, 35% di tipo D; oggi 60% sono di tipo K, 10% di tipo NK, 5% di tipo GPL, 25% di tipo D. Quale delle seguenti affermazioni è vera, supponendo che il numero totale degli autoveicoli circolanti non sia cambiato?
|
(A) CO e HC sono diminuiti, NOx è aumentato (B) CO è diminuito, HC e NOx sono aumentati (C) CO e NOx sono aumentati, HC è diminuito (D) CO e NOx sono diminuiti, HC è aumentato (E) CO, HC, NOx sono aumentati (F) CO e HC sono aumentati, NOx è diminuito (G) CO è aumentato, HC e NOx sono diminuiti (H) CO, HC, NOx sono diminuiti |
—————————————————————————
13) Siano A = 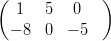 e v =
e v = 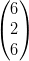 ,
,
(A) il prodotto Av esiste, il prodotto Atv non esiste
(B) il prodotto Av non esiste, il prodotto Atv esiste
(C) esistono entrambi i prodotti Av e Atv
(D) i prodotti Av e Atv non esistono
—————————————————————————
14) La seguente tabella contiene, in unità di misura fittizie, la produzione media di ossidi di carbonio CO, di idrocarburi HC, di ossidi di azoto NOx, per autoveicoli a benzina catalizzati K, non catalizzati NK, a gpl GPL, diesel D.
| K | NK | GPL | D | |
| CO | 0.1 | 2 | 2 | 0.01 |
| HC | 20 | 100 | 500 | 0.1 |
| NOx | 20 | 200 | 100 | 100 |
Dieci anni fa 50% degli autoveicoli erano di tipo K, 10% di tipo NK, 5% di tipo GPL, 35% di tipo D; oggi 60% sono di tipo K, 10% di tipo NK, 5% di tipo GPL, 25% di tipo D. Quale delle seguenti affermazioni è vera, supponendo che il numero totale degli autoveicoli circolanti sia aumentato del 20%?
|
(A) CO e HC sono aumentati, NOx è diminuito (B) CO, HC, NOx sono aumentati (C) CO, HC, NOx sono diminuiti (D) CO è aumentato, HC e NOx sono diminuiti (E) CO e NOx sono diminuiti, HC è aumentato (F) CO e NOx sono aumentati, HC è diminuito (G) CO è diminuito, HC e NOx sono aumentati (H) CO e HC sono diminuiti, NOx è aumentato |
—————————————————————————
15) Siano A = 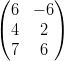 e B =
e B = 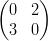 ;
;
(A) il prodotto BtAt esiste, il prodotto AtBt non esiste
(B) il prodotto AtBt esiste, il prodotto BtAt non esiste
—————————————————————————
16) Se A = 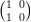 e B =
e B = 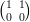
(A) i prodotti AB e BA non esistono
(B) il prodotto BA esiste, il prodotto AB non esiste
(C) i prodotti AB e BA esistono e AB = BA
(D) i prodotti AB e BA esistono e AB≠BA
(E) il prodotto AB esiste, il prodotto BA non esiste
—————————————————————————
17) Sia A una matrice quadrata 2 × 2, sia v un vettore colonna a due componenti, e a un numero reale.
(A) i prodotti aA e av non sono prodotti riga-colonna
(B) i prodotti Av e av sono prodotti riga-colonna
(C) i prodotti Av e aA sono prodotti riga-colonna
—————————————————————————
18) Sia A = 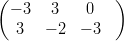 e B =
e B = 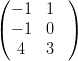 .
.
|
(A) A + B esiste e At + B non esiste (B) At + B esiste e A + B non esiste |
—————————————————————————
19) Se A è una matrice 2 × 3 e v un vettore colonna di 3 elementi, il prodotto Atv esiste.
|
(A) falso (B) vero |
—————————————————————————
20) 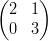 ⋅
⋅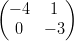 =
= 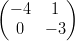 ⋅
⋅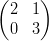
|
(A) falso (B) vero |
—————————————————————————
21) Sia A = 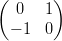 e siano v =
e siano v = 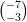 e w =
e w = 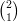 . Il prodotto w ⋅ Av è nullo?
. Il prodotto w ⋅ Av è nullo?
|
(A) si (B) no |
—————————————————————————
22) Sia A = 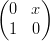 . Per quali valori di x vale A3 =
. Per quali valori di x vale A3 = 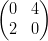 ? Ricordo che A3 = AAA, nel senso del
prodotto righe-colonne.
? Ricordo che A3 = AAA, nel senso del
prodotto righe-colonne.
(A) nessun valore di x
(B) 8
(C) 1
(D) 2
(E) 0
—————————————————————————
|
1 C 2 A 3 B 4 A 5 D 6 A 7 A 8 D 9 D 10 E 11 A 12 F 13 A 14 B 15 A 16 D 17 A 18 B 19 A 20 B 21 B 22 D |
1) Dati i vettori v = 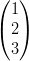 e w =
e w = 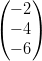 , esiste a
, esiste a 
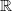 tale che w = av?
tale che w = av?
|
(A) si (B) no |
—————————————————————————
2) Il sistema
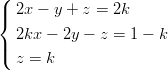
(A) nessuna soluzione se k≠2 e infinite soluzioni se k = 2
(B) una sola soluzione se k≠2 e nessuna soluzione se k = 2
(C) infinite soluzioni se k≠2 e una sola soluzione se k = 2
(D) infinite soluzioni se k≠2 e nessuna soluzione se k = 2
(E) nessuna soluzione se k≠2 e una sola soluzione se k = 2
(F) una sola soluzione se k≠2 e infinite soluzioni se k = 2
—————————————————————————
3) Dati i vettori v = 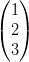 e w =
e w = 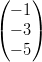 , esiste a
, esiste a 
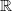 tale che av +
tale che av + 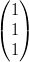 = w?
= w?
|
(A) si (B) no |
—————————————————————————
4) Il sistema
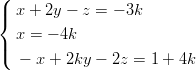
(A) nessuna soluzione se k≠2 e una sola soluzione se k = 2
(B) infinite soluzioni se k≠2 e una sola soluzione se k = 2
(C) una sola soluzione se k≠2 e infinite soluzioni se k = 2
(D) una sola soluzione se k≠2 e nessuna soluzione se k = 2
(E) infinite soluzioni se k≠2 e nessuna soluzione se k = 2
(F) nessuna soluzione se k≠2 e infinite soluzioni se k = 2
—————————————————————————
5) Siano p = 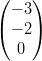 , q =
, q = 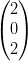 , e v =
, e v = 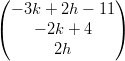 ; per quali valori di k e h il vettore v è
ortogonale ad entrambi i vettori p e q?
; per quali valori di k e h il vettore v è
ortogonale ad entrambi i vettori p e q?
(A) k = -1, h = 2
(B) nessun valore di k e h
(C) k = -1, e h qualunque
(D) h = -1, e k qualunque
(E) k = 2, h = -1
(F) h = 2, e k qualunque
(G) k = 2, e h qualunque
—————————————————————————
6) Siano v = 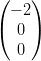 , w =
, w = 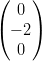 , p =
, p = 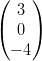 . Esistono a,b
. Esistono a,b 
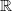 tali che av + bw = p?
tali che av + bw = p?
|
(A) no (B) si |
—————————————————————————
7) Il sistema 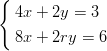
(A) non ha soluzioni per r≠2 ed ha infinite soluzioni per r = 2
(B) ha una sola soluzione per r≠2 e non ha soluzioni per r = 2
(C) ha infinite soluzioni per r≠2 ed ha una sola soluzione per r = 2
(D) ha infinite soluzioni per r≠2 e non ha soluzioni per r = 2
(E) ha una sola soluzione per r≠2 ed ha infinite soluzioni per r = 2
(F) non ha soluzioni per r≠2 ed ha una sola soluzione per r = 2
—————————————————————————
8) Il sistema 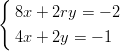
(A) ha infinite soluzioni per r≠2 e non ha soluzioni per r = 2
(B) non ha soluzioni per r≠2 ed ha una sola soluzione per r = 2
(C) ha una sola soluzione per r≠2 ed ha infinite soluzioni per r = 2
(D) ha una sola soluzione per r≠2 e non ha soluzioni per r = 2
(E) non ha soluzioni per r≠2 ed ha infinite soluzioni per r = 2
(F) ha infinite soluzioni per r≠2 ed ha una sola soluzione per r = 2
—————————————————————————
9) Il sistema, nelle variabili p e q, 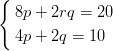
(A) non ha soluzioni per r≠2 ed ha una sola soluzione per r = 2
(B) ha una sola soluzione per r≠2 ed ha infinite soluzioni per r = 2
(C) ha una sola soluzione per r≠2 e non ha soluzioni per r = 2
(D) ha infinite soluzioni per r≠2 e non ha soluzioni per r = 2
(E) non ha soluzioni per r≠2 ed ha infinite soluzioni per r = 2
(F) ha infinite soluzioni per r≠2 ed ha una sola soluzione per r = 2
—————————————————————————
10) Sia A = 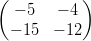 . L’unico vettore
. L’unico vettore 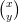 per cui A
per cui A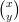 =
= 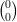 è il vettore
è il vettore 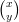 =
= 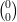
|
(A) falso (B) vero |
—————————————————————————
11) Il sistema
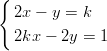
(A) infinite soluzioni se k≠2 e una sola soluzione se k = 2
(B) nessuna soluzione se k≠2 e una sola soluzione se k = 2
(C) nessuna soluzione se k≠2 e infinite soluzioni se k = 2
(D) infinite soluzioni se k≠2 e nessuna soluzione se k = 2
(E) una sola soluzione se k≠2 e infinite soluzioni se k = 2
(F) una sola soluzione se k≠2 e nessuna soluzione se k = 2
—————————————————————————
12) Dati i vettori v = 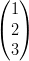 e w =
e w = 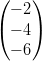 , esiste a
, esiste a 
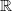 tale che w = av?
tale che w = av?
|
(A) si (B) no |
—————————————————————————
13) Discutere il numero delle soluzioni al variare di k 
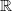 del sistema
del sistema
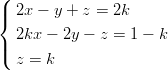
(A) infinite soluzioni se k≠2 e nessuna soluzione se k = 2
(B) una sola soluzione se k≠2 e nessuna soluzione se k = 2
(C) una sola soluzione se k≠2 e infinite soluzioni se k = 2
(D) nessuna soluzione se k≠2 e infinite soluzioni se k = 2
(E) nessuna soluzione se k≠2 e una sola soluzione se k = 2
(F) infinite soluzioni se k≠2 e una sola soluzione se k = 2
—————————————————————————
14) Per quali valori di k i vettori v = 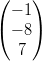 e w =
e w = 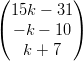 sono ortogonali?
sono ortogonali?
|
(A) per k = 2 (B) per k = 0 (C) per k = -2 (D) per nessun valore di k |
—————————————————————————
15) Il sistema 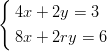
(A) non ha soluzioni per r≠2 ed ha una sola soluzione per r = 2
(B) ha infinite soluzioni per r≠2 e non ha soluzioni per r = 2
(C) non ha soluzioni per r≠2 ed ha infinite soluzioni per r = 2
(D) ha una sola soluzione per r≠2 ed ha infinite soluzioni per r = 2
(E) ha infinite soluzioni per r≠2 ed ha una sola soluzione per r = 2
(F) ha una sola soluzione per r≠2 e non ha soluzioni per r = 2
—————————————————————————
16) Il vettore x = 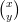 soddisfa
soddisfa 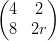 x =
x = 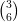 , dove r è un parametro reale. Quanti vettori x
esistono che soddisfano tale relazione?
, dove r è un parametro reale. Quanti vettori x
esistono che soddisfano tale relazione?
(A) r≠ 2 infiniti, e per r = 2 nessuno
(B) per r≠2 infiniti, e per r = 2 uno solo
(C) per r≠2 nessuno, e per r = 2 infiniti
(D) per r≠2 nessuno, e per r = 2 uno solo
(E) per r≠2 uno solo, e per r = 2 nessuno
(F) per r≠2 uno solo, e r = 2 infiniti
—————————————————————————
17) Il sistema
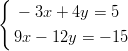
|
(A) non ha soluzioni (B) ha una sola soluzione (C) ha infinite soluzioni |
—————————————————————————
|
1 A 2 B 3 A 4 D 5 A 6 A 7 E 8 C 9 B 10 A 11 F 12 A 13 B 14 D 15 D 16 F 17 C |
1) La disequazione 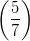 2x+2 > 1 ha soluzione x < z, con z opportuno numero reale. Determinare il
valore di z.
2x+2 > 1 ha soluzione x < z, con z opportuno numero reale. Determinare il
valore di z.
(Si ricordi che log a < 0 se 0 < a < 1 .)
|
(A) -2 (B) -1 (C) -3 (D) 1 (E) 3 |
—————————————————————————
2) La disequazione 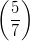 2x+2 > 1 ha soluzione x < z, con z opportuno numero reale. Determinare il
valore di z.
2x+2 > 1 ha soluzione x < z, con z opportuno numero reale. Determinare il
valore di z.
(Si ricordi che log a < 0 se 0 < a < 1 .)
|
(A) -1 (B) 3 (C) 1 (D) -2 (E) -3 |
—————————————————————————
3) Sia a > 0. La disequazione 2a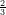 > 3a
> 3a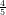 ha come soluzione
ha come soluzione
(A) a > 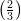
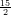
(B) a < 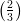
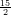
(C) nessuna delle altre
(D) a > 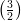
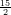
(E) a < 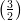
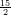
—————————————————————————
4) La disequazione 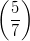 2x+2 > 1 ha soluzione x < z, con z opportuno numero reale. Determinare il
valore di z.
2x+2 > 1 ha soluzione x < z, con z opportuno numero reale. Determinare il
valore di z.
(Si ricordi che log a < 0 se 0 < a < 1 .)
|
(A) 3 (B) 1 (C) -3 (D) -2 (E) -1 |
—————————————————————————
5) La disequazione 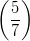 2x+2 > 1 ha soluzione x < z, con z opportuno numero reale. Determinare il
valore di z.
2x+2 > 1 ha soluzione x < z, con z opportuno numero reale. Determinare il
valore di z.
(Si ricordi che log a < 0 se 0 < a < 1 .)
|
(A) 1 (B) -2 (C) -1 (D) 3 (E) -3 |
—————————————————————————
6) La disequazione e4 - e2x+3 > 0 ha come soluzione
|
(A) x < 2 (B) x > (C) x < 0 (D) x < (E) x > 0 (F) x > 2 |
—————————————————————————
7) La disequazione log(x + 4) > 1 ha soluzione
|
(A) x > -4 (B) x > 3 (C) x > e - 4 (D) x > 0 (E) x > 5 |
—————————————————————————
8) Per ogni r < 2, vale |r - 2| < 0;
|
(A) vero (B) falso |
—————————————————————————
9) e2 ln x-3 =
|
(A) x-6 (B) ln x-6 (C) ln x-1 (D) e2 + x-3 (E) x-1 (F) 2 + x-3 |
—————————————————————————
10) Se r < 2, allora |r - 2| = r - 2;
|
(A) vero (B) falso |
—————————————————————————
11) Per ogni a > 0 vale | log a| = log |a|
|
(A) vero (B) falso |
—————————————————————————
12) Per ogni a,b > 0 vale log(a + b) = log a + log b
|
(A) falso (B) vero |
—————————————————————————
13) Per ogni x 
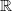 , ex-1 > 0
, ex-1 > 0
|
(A) vero (B) falso |
—————————————————————————
14) Per ogni a, b vale ea+b = ea + eb
|
(A) vero (B) falso |
—————————————————————————
15) La funzione e-x2-9x-20 è positiva e non nulla per ogni valore di x 
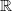 .
.
|
(A) falso (B) vero |
—————————————————————————
16) Sia f(x) = e-x2-9x-20 e g(x) = ex2-7x+12. Vale f(x) + g(x) = e-16x-8
|
(A) vero (B) falso |
—————————————————————————
17) Per r > 0, la disequazione r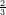 < e
< e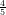 ha soluzione
ha soluzione
|
(A) r > 1 (B) r < 1 |
—————————————————————————
18) La disequazione | 2r + 1|≤ 1 ha come soluzione
(A) |r| ≤
(B) -1 ≤ r ≤-
(C) - ≤ r ≤ 0
≤ r ≤ 0
(D) |r| ≤
(E) -1 ≤ r ≤ 0
—————————————————————————
19) I valori di x per cui ln(-x2 + 3x) > - ln 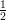 sono tutti e soli:
sono tutti e soli:
|
(A) x < 1 e x > 2 (B) 0 < x < 3 (C) x < 0 e x > 3 (D) x < 0 e x > 2 (E) 1 < x < 2 (F) 1 < x < 3 (G) 0 < x < 2 (H) x < 1 e x > 3 |
—————————————————————————
20) Per ogni a,b > 0 vale log(a + b) = log a + log b
|
(A) vero (B) falso |
—————————————————————————
21) e2 ln x-3 =
|
(A) e2 + x-3 (B) x-6 (C) x-1 (D) ln x-1 (E) ln x-6 (F) 2 + x-3 |
—————————————————————————
|
1 B 2 A 3 B 4 E 5 C 6 D 7 C 8 B 9 A 10 B 11 B 12 A 13 A 14 B 15 B 16 B 17 A 18 E 19 E 20 B 21 B |
1) In un fenomeno di crescita ( o decrescita) lineare, vengono misurati i seguenti valori della grandezza x
in funzione del tempo t: x = -1 per t = 2, e x = -3 per t = 5. Per quale valore di t si ottiene x(t) = 9?
|
(A) 5 (B) -13 (C) -8 (D) -11 (E) 17 |
—————————————————————————
2) Una legge empirica afferma che le prestazioni dei calcolatori raddoppiano ogni anno e mezzo.
Attualmente la dimensione tipica di un grande disco rigido è di 40960 Megabyte. Quant’era (in Megabyte) 3 anni fa?
|
(A) 10240 (B) 32 (C) 40 (D) 128 (E) 2 |
—————————————————————————
3) Un gatto ed un cane sono alla distanza di 10 metri.
All’istante t = 0 il cane comincia a correre verso il gatto a 11 ms-1.
Al tempo t = 1∕2 secondi il gatto fugge nella direzione opposta al cane, alla velocità di 8 ms-1 .
La funzione d(t) =“distanza tra il cane e il gatto”, in metri, per t ≥ 0 è
(A)
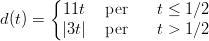
(B)
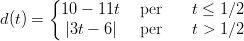
(C)
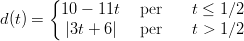
(D) nessuna delle altre
(E)
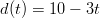
—————————————————————————
4) In un esperimento viene misurata una quantità A in funzione di una quantità B. Supponendo di osservare
A = 20 se B = 1, e A = 18 se B = 2, e supponendo che la legge sia lineare, quanto si dovrebbe osservare per B = 7?
|
(A) 30 (B) 6 (C) 32 (D) 8 |
—————————————————————————
5) In una reazione nucleare il numero di neutroni liberi raddoppia in 20 secondi.
In quanti minuti il numero di neutroni aumenta di 23 volte?
|
(A) 23 ∕3 (B) 2 (C) 1 (D) 23 ∕6 (E) 3∕ log 6 (F) 3 log 2∕ log 6 |
—————————————————————————
6) Nello studio di un certo fenomeno, si ipotizza che la quantità p dipenda con una legge lineare da una quantità q. Supponendo di misurare p = 7 per q = 1, e p = 3 per q = 2, per quale valore di q si misurerebbe p = 1?
|
(A) 11 (B) (C) 4 (D) - (E) (F) |
—————————————————————————
7) In un modello elementare per il calcolo dello spazio di frenata di un veicolo, si suppone che il
freno agisca con decelerazione costante. La legge del moto di un tal veicolo sarebbe dunque
s(t) = s0 + v0t -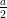 t2, per t > 0, dove 0 è l’istante in cui il freno cominicia ad agire, s
0 e v0 lo spazio
percorso e la velocità all’istante 0. Lo spazio di frenata è lo spazio percorso dal tempo 0 all’istante in
cui il veicolo si ferma (velocità nulla). Supponendo che per un certo veicolo lo spazio di frenata per una
velocità di 18 Kmh-1 è di 9 metri, quanto sarà lo spazio di frenata per una velocità di
24Km h-1?
t2, per t > 0, dove 0 è l’istante in cui il freno cominicia ad agire, s
0 e v0 lo spazio
percorso e la velocità all’istante 0. Lo spazio di frenata è lo spazio percorso dal tempo 0 all’istante in
cui il veicolo si ferma (velocità nulla). Supponendo che per un certo veicolo lo spazio di frenata per una
velocità di 18 Kmh-1 è di 9 metri, quanto sarà lo spazio di frenata per una velocità di
24Km h-1?
|
(A) 18 (B) 13 (C) 25 (D) 12 (E) 16 (F) 19 |
—————————————————————————
8) Una popolazione batterica è inizialmente formata da 2 ⋅ 106 batteri. Essa, nutrita con una certa sostanza, raddoppia in 2 ⋅ ln 2 giorni. Il consumo istantaneo, per ogni batterio, di questa sostanza è di 2 ⋅ 10-9 grammi al giorno. Supponendo di avere a disposizione un grammo di sostanza, per quanti giorni si può mantenere la popolazione con questo ritmo di crescita? (Per semplicità si consideri la numerosità una variabile continua).
(A) 2 ln 250 ≃ 11.0429
(B)  ≃ 40.8999
≃ 40.8999
(C) 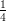 ⋅ 1000 ⋅ ln 2 ≃ 173.2868
⋅ 1000 ⋅ ln 2 ≃ 173.2868
(D) 2 ln 126 ≃ 9.6726
(E) 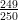 ⋅ 103 ≃ 996.00
⋅ 103 ≃ 996.00
—————————————————————————
9) Nello studio di un certo fenomeno, si ipotizza che la quantità p dipenda con una legge lineare da una quantità q. Viene misurato p = 7 per q = 1, e p = 3 per q = 2. Quanto vale p per q = 4?
|
(A) (B) -5 (C) (D) (E) 3 (F) 19 |
—————————————————————————
10) Una legge lineare lega le variabili p e q. Sapendo che se p aumenta di 2, q aumenta di 6, e che per p = 3 si ha q = 13, quanto vale q per p = -3?
|
(A) 13 (B) -13 (C) -5 (D) -9 |
—————————————————————————
11) Una certa quantità q decresce esponenzialmente nel tempo, cioè segue una legge del tipo q(t) = ae-bt, con b > 0. Sapendo che q = 2 al tempo 0, e che q = 2e-12 al tempo 4, quanto vale q al tempo 1?
(A) 2e-3
(B) 2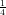 e-3
e-3
(C) 2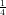 e-12
e-12
(D) 8e-3
(E) 8e-12
(F) 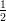 e-12
e-12
(G) 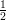 e-3
e-3
—————————————————————————
12) La massa di una coltura batterica, inizialmente uguale ad 1, aumenta del 10% ogni 2 giorni. Quanto vale dopo 4 giorni?
|
(A) (B) (C) (D) |
—————————————————————————
13) Una legge lineare lega le variabili p e q. Sapendo che se p aumenta di 2, q aumenta di 6, e che per p = 3 si ha q = 13, per quale valore di p si ha q = -3?
|
(A) -5 (B) -21 (C) - (D) 3 |
—————————————————————————
14) Una certa quantità q decresce esponenzialmente nel tempo. Sapendo che q = 2e-12 al tempo t = 4,
e che q = 2e-3 al tempo t = 1, quanto vale q al tempo t = 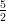 ?
?
(A) 1e-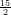
(B) 1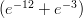
(C) 2e-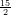
—————————————————————————
15) La numerosità di una coltura batterica aumenta del 10% ogni 2 giorni. Di quanto è aumentata dopo 4 giorni?
|
(A) 121% (B) 21% (C) 20% (D) 1% (E) 120% (F) 220% |
—————————————————————————
16) Sia y = f(x) una legge lineare, di coefficiente angolare -2. È noto che f(-4) = 11. Quanto vale f(5)?
|
(A) 1 (B) -7 (C) 8 (D) -10 (E) -18 |
—————————————————————————
17) Durante il picco dell’epidemia, il numero N di casi di SARS aumentava di 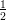 N ogni 2 giorni. Di
quanto aumentava in 4 giorni?
N ogni 2 giorni. Di
quanto aumentava in 4 giorni?
(A)  N
N
(B) 1N
(C) 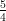 N
N
(D) 3N
(E) 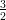 N
N
—————————————————————————
18) In un campione di materiale radioattivo, la massa totale m decresce esponenzialmente nel tempo. Sapendo che m = 2 al tempo 0, e che m = 2e-12 al tempo 4, quanto vale m al tempo 1?
(A) 8e-12
(B) 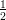 e-3
e-3
(C) 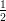 e-12
e-12
(D) 8e-3
(E) 2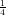 e-12
e-12
(F) 2e-3
(G) 2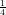 e-3
e-3
—————————————————————————
19) Durante il picco dell’epidemia SARS, il numero N di casi aumentava di 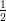 N ogni 2 giorni.
Quant’era il numero di casi dopo 3 giorni, se inizialmente era N?
N ogni 2 giorni.
Quant’era il numero di casi dopo 3 giorni, se inizialmente era N?
(A) 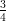 N
N
(B)  N
N
(C) 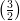
 N
N
(D) 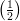
 N
N
—————————————————————————
20) La massa m(t) di un isotopo radioattivo decresce esponenzialmente nel tempo. È noto che
m(0) = 4, e m(2) =  . Quanto vale m(1)?
. Quanto vale m(1)?
|
(A) (B) 4e-2 (C) 1 |
—————————————————————————
21) Si supponga che la numerosità della popolazione mondiale segua una legge esponenziale. Nell’anno 1850 la numerosità era di 0.5 miliardi. Supponendo che la popolazione raddoppi in 9 anni, durante quale anno essa ha raggiunto 0.75 miliardi?
|
(A) 1856 (B) 1853 (C) 1855 (D) 1854 |
—————————————————————————
22) Nello studio di un certo fenomeno, si ipotizza che la quantità p dipenda con una legge lineare da una quantità q. Supponendo di misurare p = 7 per q = 1, e p = 3 per q = 2, per quale valore di q si misurerebbe p = 1?
|
(A) 4 (B) 11 (C) (D) - (E) (F) |
—————————————————————————
23) Negli ultimi 4 anni, i prezzi sono aumentati del 2.3 % all’anno. Di quanto sono aumentati in totale?
|
(A) 9.68 % (B) 9.36 % (C) 9.52 % (D) 9.20 % |
—————————————————————————
24) Ogni 3 giorni, 1/4 dei nuclei di un isotopo radioattivo decade. Dopo quanti giorni è decaduta la metà dei nuclei?
|
(A) 24 (B) 3 (C) (D) 3 log (E) 3 log (F) 8 (G) 3 (H) |
—————————————————————————
25) Una quantità p varia con il tempo t, e viene misurata tre volte, ottenendo:
| t | p |
| 1 | 1 |
| 2 | 4 |
| 4 | 11 |
I dati sono compatibili con l’ipotesi che p dipenda da t con una legge lineare?
|
(A) si (B) no |
—————————————————————————
26) Una quantità p varia con il tempo t, e viene misurata tre volte, ottenendo:
| t | p |
| 1 | 1 |
| 2 | 2 |
| 4 | 10 |
I dati sono compatibili con l’ipotesi che p dipenda da t con una legge esponenziale?
|
(A) no (B) si |
—————————————————————————
|
1 B 2 A 3 B 4 D 5 C 6 B 7 E 8 D 9 B 10 C 11 A 12 B 13 C 14 C 15 B 16 B 17 C 18 F 19 C 20 C 21 C 22 F 23 C 24 G 25 B 26 A |
1) Il dominio di definizione di f(x) = log(2 + |x|) è
|
(A) tutta la retta reale (B) x > 0 (C) x > -2 |
—————————————————————————
2) Il punto (k, 2) appartiene al grafico della funzione f(x) = 2 log(x + 1) per
|
(A) k = e - 1 (B) nessun valore di k (C) k = 2 log 3 |
—————————————————————————
3)
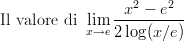
|
(A) è e2 (B) è e (C) è 0 |
—————————————————————————
4) Calcolare il limite
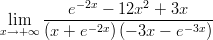
|
(A) 4 (B) -2 (C) 3 (D) -3 |
—————————————————————————
5) Il limite per x → +∞ della funzione f(x) = 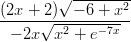 è:
è:
|
(A) +∞ (B) 0 (C) 1 (D) -1 (E) -∞ |
—————————————————————————
6) lim r→+∞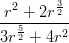 vale:
vale:
(A) nessuna delle altre
(B) +∞;
(C) 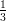 ;
;
(D) 0;
(E) 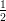 ;
;
(F)  ;
;
(G) 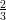 ;
;
—————————————————————————
7) lim r→0+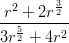 vale:
vale:
(A) +∞;
(B)  ;
;
(C) 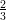 ;
;
(D) 0;
(E) nessuna delle altre
(F) 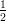 ;
;
(G) 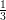 ;
;
—————————————————————————
8) lim x→+∞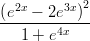 è
è
(A) 4
(B) 5
(C) 1
(D) 2
(E) +∞
(F) 0
(G) -2
—————————————————————————
9) lim r→+∞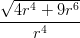 =
=
|
(A) 0 (B) 4 (C) 3 (D) 2 (E) 9 (F) +∞ |
—————————————————————————
10) lim c→+∞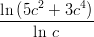 è
è
|
(A) 3 (B) 0 (C) 5 (D) +∞ (E) 2 (F) 4 |
—————————————————————————
11)
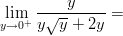
|
(A) ∞ (B) (C) (D) 0 (E) - (F) - |
—————————————————————————
12) lim x→-∞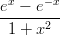 è
è
|
(A) +∞ (B) 0 (C) -1 (D) 1 (E) non esiste (F) -∞ |
—————————————————————————
13) Il limite per x → +∞ della funzione f(x) = 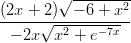 è:
è:
|
(A) +∞ (B) -1 (C) 0 (D) 1 (E) -∞ |
—————————————————————————
14) Per x → 0, x va a 0 più rapidamente di x
va a 0 più rapidamente di x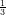
|
(A) vero (B) falso |
—————————————————————————
15) Siano f1(x) = 5x2 - 6, f
2(x) = 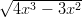 , f3(x) = 8e
, f3(x) = 8e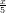 ; il loro limite per x → +∞è +∞. Quale
dei seguenti è il loro ordinamento, da quella che diverge piú rapidamente a quella che diverge meno
rapidamente?
; il loro limite per x → +∞è +∞. Quale
dei seguenti è il loro ordinamento, da quella che diverge piú rapidamente a quella che diverge meno
rapidamente?
|
(A) f3 , f1, f2 (B) f3 , f2, f1 (C) f2 , f1, f3 (D) f2 , f3, f1 (E) f1 , f3, f2 (F) f1 , f2, f3 |
—————————————————————————
16) Per x → +∞, 2x3e2x va a infinito piú rapidamente di 3x2e3x
|
(A) falso (B) vero |
—————————————————————————
17) Siano f1(x) = 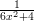 , f2(x) =
, f2(x) = 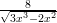 , f3(x) = 4e-
, f3(x) = 4e- ; il loro limite per x → +∞è 0. Quale dei
seguenti è il loro ordinamento, da quella che va a zero piú rapidamente a quella che va a zero meno
rapidamente?
; il loro limite per x → +∞è 0. Quale dei
seguenti è il loro ordinamento, da quella che va a zero piú rapidamente a quella che va a zero meno
rapidamente?
|
(A) f3 , f2, f1 (B) f1 , f3, f2 (C) f1 , f2, f3 (D) f2 , f3, f1 (E) f2 , f1, f3 (F) f3 , f1, f2 |
—————————————————————————
18) Sia f(x) = (-2x2 + x - 3)e-x2 e g(x) = (-x2 + x - 3)e-x2. Per x → +∞, f(x) va a zero piú rapidamente di g(x)
|
(A) vero (B) falso |
—————————————————————————
19) lim x→-∞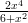 è
è
(A) -2
(B) 2
(C) -∞
(D) 1
(E) -1
(F) +∞
(G) 0
—————————————————————————
20) Sia a > 0 e f(x) = 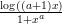 . Sia g(x) =
. Sia g(x) = 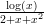 . Per x → +∞, f va a 0 più rapidamente di g se e
solo se:
. Per x → +∞, f va a 0 più rapidamente di g se e
solo se:
|
(A) a ≤ 2 (B) a ≥ 2 (C) a < 2 (D) a > 2 |
—————————————————————————
21) Sia f(x) = (-2x2 + x - 3)ex e g(x) = (-x2 + x - 3)ex. Per x →-∞, f(x) va a zero piú rapidamente di g(x)
|
(A) falso (B) vero |
—————————————————————————
22) lim x→+∞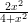 è
è
|
(A) -2 (B) +∞ (C) -1 (D) 2 (E) 0 (F) 1 |
—————————————————————————
23) Sia a > 0 e f(x) = 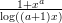 . Sia g(x) =
. Sia g(x) = 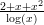 . Per x → +∞, f va a +∞ più rapidamente di g se
e solo se:
. Per x → +∞, f va a +∞ più rapidamente di g se
e solo se:
|
(A) a > 2 (B) a ≥ 2 (C) a < 2 (D) a ≤ 2 |
—————————————————————————
24) Sia f(x) = e-x2-9x-20, e g(x) = e-x2+7x-12. Per x → +∞
|
(A) f va a zero più rapidamente di g (B) g va a zero più rapidamente di f |
—————————————————————————
25) Il limite di ex2+9x+20, per x →-∞è
|
(A) 0 (B) -∞ (C) +∞ |
—————————————————————————
26) Il limite per x → +∞ di 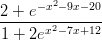 è
è
|
(A) 2 (B) 0 (C) (D) +∞ |
—————————————————————————
27) Si considerino le funzioni f1(x) = (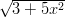 + x3)5, f
2(x) = (
+ x3)5, f
2(x) = (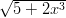 + x5)2,
f3 (x) = (
+ x5)2,
f3 (x) = (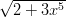 + x2)3. Il loro ordinamento, da quella che diverge meno velocemente a quella che
diverge più velocemente per x → +∞è
+ x2)3. Il loro ordinamento, da quella che diverge meno velocemente a quella che
diverge più velocemente per x → +∞è
|
(A) f3 f1 f2 (B) f2 f1 f3 (C) f1 f2 f3 (D) f2 f3 f1 (E) f3 f2 f1 (F) f1 f3 f2 |
—————————————————————————
28) Si considerino le funzioni f1(x) = xe-x, f
2(x) = x2e-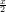 , f3(x) = x2e-x Il loro ordinamento, da
quella che va a zero più velocemente a quella che va a zero più lentamente, per x → +∞
è
, f3(x) = x2e-x Il loro ordinamento, da
quella che va a zero più velocemente a quella che va a zero più lentamente, per x → +∞
è
|
(A) f2 f1 f3 (B) f3 f2 f1 (C) f1 f2 f3 (D) f1 f3 f2 (E) f2 f3 f1 (F) f3 f1 f2 |
—————————————————————————
29) Per x → 0, x va a 0 più rapidamente di x
va a 0 più rapidamente di x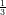
|
(A) falso (B) vero |
—————————————————————————
30) Siano f1(x) = 5x2 - 6, f
2(x) = 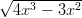 , f3(x) = 8e
, f3(x) = 8e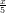 ; il loro limite per x → +∞è +∞. Quale
dei seguenti è il loro ordinamento, da quella che diverge piú rapidamente a quella che diverge meno
rapidamente?
; il loro limite per x → +∞è +∞. Quale
dei seguenti è il loro ordinamento, da quella che diverge piú rapidamente a quella che diverge meno
rapidamente?
|
(A) f3 , f2, f1 (B) f2 , f3, f1 (C) f1 , f3, f2 (D) f3 , f1, f2 (E) f1 , f2, f3 (F) f2 , f1, f3 |
—————————————————————————
31) Per x → +∞, la funzione e-3x+2 va a 0 più lentamente della funzione e-6x-5
|
(A) vero (B) falso |
—————————————————————————
32) Sia f(x) = -2e-3x + 4e5x. Quanto vale lim x→-∞f(x)?
|
(A) 0 (B) 1 (C) +∞ (D) -∞ |
—————————————————————————
33) lim x→+∞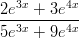 =
=
|
(A) (B) 0 (C) (D) +∞ |
—————————————————————————
34) lim x→-∞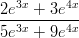 =
=
|
(A) 0 (B) +∞ (C) (D) |
—————————————————————————
35)
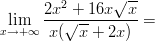
|
(A) 8 (B) 16 (C) 1 (D) 2 |
—————————————————————————
36)
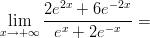
|
(A) 3 (B) 6 (C) 1 (D) +∞ (E) 2 (F) 0 |
—————————————————————————
37)
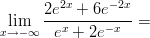
|
(A) 2 (B) 1 (C) 3 (D) 0 (E) 6 (F) +∞ |
—————————————————————————
|
1 A 2 A 3 A 4 A 5 D 6 D 7 A 8 E 9 A 10 F 11 B 12 F 13 B 14 A 15 A 16 A 17 F 18 B 19 F 20 D 21 A 22 D 23 A 24 A 25 C 26 B 27 E 28 D 29 B 30 D 31 A 32 D 33 C 34 C 35 C 36 D 37 F |
1) La funzione f(x) = 2x3 + 3x2 nell’intervallo [-1,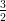 ]
]
(A) ha massimo e minimo assoluti all’interno dell’intervallo di definizione
(B) ha il massimo assoluto all’interno dell’intervallo di definizione e il minimo assoluto in uno degli estremi
(C) ha il minimo assoluto all’interno dell’intervallo di definizione e il massimo assoluto in uno degli estremi
—————————————————————————
2) La retta tangente al grafico della funzione f(x) = (-2x + 3)e-2x nel punto x 0 = 1 è: e-2 (z - 4x),
con z opportuno numero reale. Determinare il valore di z.
|
(A) 16 (B) 5 (C) -1 (D) 7 (E) -5 |
—————————————————————————
3) Calcolare per quale valore di x la funzione f(x) =  x3 - 12x - 2x2 + 2 raggiunge il suo unico
minimo relativo.
x3 - 12x - 2x2 + 2 raggiunge il suo unico
minimo relativo.
|
(A) 6 (B) 1 (C) 5 (D) -1 (E) -5 |
—————————————————————————
4) La derivata della funzione f(s) = 4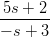 in s = 1 è
in s = 1 è
|
(A) 13 (B) 17 (C) 26 (D) 34 |
—————————————————————————
5) Sia f(r) = 4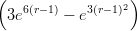 -2. La retta tangente al grafico nel punto r = 1 è:
-2. La retta tangente al grafico nel punto r = 1 è:
|
(A) 19 - 18r (B) -17 + 18r (C) 1 - 18r (D) 18 + 18r (E) 18 - 18r (F) 1 + 18r |
—————————————————————————
6) La funzione f(x) = -6e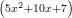
(A) ha un minimo relativo in x = -1
(B) ha un massimo relativo in x = -1
(C) non ha né un massimo né un minimo in x = -1
—————————————————————————
7) La funzione f(z) = z4 + z3 + 2z2 + 4
(A) ha un minimo relativo e nessun massimo relativo
(B) ha un massimo relativo e due minimi relativi
(C) ha un massimo relativo e un minimo relativo
(D) non ha né massimi né minimi relativi
(E) ha un massimo relativo e nessun minimo relativo
(F) ha due massimi relativi e un minimo relativo
—————————————————————————
8) Si consideri la funzione f(r) = 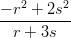 , dove s è un parametro reale non nullo.
, dove s è un parametro reale non nullo. 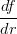 (r), calcolata
nel punto r = s vale:
(r), calcolata
nel punto r = s vale:
(A) -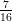
(B) nessuna delle precedenti
(C) - s
s
(D) -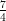
(E) -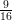
(F) -
(G) -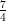 s
s
—————————————————————————
9) La funzione f(v) = |- v2 - 5v - 6|è
(A) decrescente per v < -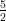 e crescente per v > -
e crescente per v > -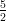
(B) decrescente per -3 < v < - , crescente per v < -3 e v > -
, crescente per v < -3 e v > -
(C) decrescente per v < -3 e - < v < -2, crescente per -3 < v < -
< v < -2, crescente per -3 < v < - e v > -2
e v > -2
(D) decrescente per -3 < v < -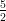 e v > -3, crescente per v < -3 e -
e v > -3, crescente per v < -3 e -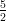 < v < -2
< v < -2
(E) decrescente per v < -3 e v > - , crescente per -3 < v < -
, crescente per -3 < v < -
(F) decrescente per v > - e crescente per v < -
e crescente per v < -
—————————————————————————
10) La funzione f(x) = 3ex + 4e-2x, con x 
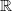
(A) ha due punti di massimo locale e nessun punto di minimo locale
(B) ha un punto di massimo e un punto di minimo locale
(C) ha un punto di massimo locale e nessun punto di minimo locale
(D) ha due punti di massimo locale e due punti di minimo locale
(E) ha due punti di minimo locale e nessun punto di massimo locale
(F) ha due punti di massimo locale e un punto di minimo locale
(G) ha due punti di minimo locale e un punto di massimo locale
(H) non ha né punti di massimo né punti di minimo locali
(I) ha un punto di minimo locale e nessun punto di massimo locale
—————————————————————————
11) La funzione f(x) = 2x3 ln (4x), definita per x > 0
(A) decresce in (0, +∞)
(B) cresce in (0, +∞)
(C) decresce in ( , +∞), cresce altrove
, +∞), cresce altrove
(D) cresce in (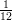 , +∞), decresce altrove
, +∞), decresce altrove
(E) decresce in (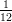 , +∞), cresce altrove
, +∞), cresce altrove
(F) cresce in ( e-
e-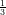 , +∞), decresce altrove
, +∞), decresce altrove
(G) cresce in (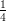 e-
e-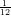 , +∞), decresce altrove
, +∞), decresce altrove
(H) cresce in (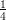 , +∞), decresce altrove
, +∞), decresce altrove
(I) decresce in ( e-
e-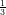 , +∞), cresce altrove
, +∞), cresce altrove
(J) decresce in (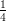 e-
e-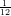 , +∞), cresce altrove
, +∞), cresce altrove
—————————————————————————
12) La funzione f(x) = 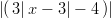
(A) è crescente in (-∞,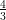 ) e decrescente altrove
) e decrescente altrove
(B) è crescente in (-∞, ) e (3,
) e (3,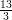 ) e decrescente altrove
) e decrescente altrove
(C) è crescente in (-∞, 3) e decrescente altrove
(D) è crescente in (4, +∞) e decrescente altrove
(E) è crescente in ( , 3) e (
, 3) e (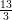 , +∞) e decrescente altrove
, +∞) e decrescente altrove
(F) è crescente in (-∞, 4) e decrescente altrove
(G) è crescente in (3, +∞) e decrescente altrove
(H) è crescente in ( , +∞) e decrescente altrove
, +∞) e decrescente altrove
—————————————————————————
13) La funzione f(x) = 2x3 - 9x2 + 12x + 1
(A) ha in x = 1 il suo unico minimo relativo e in x = 2 il suo unico massimo relativo
(B) ha in x = 1 il suo unico massimo relativo e in x = 2 il suo unico minimo relativo
(C) ha in x = 2 il suo unico minimo relativo e non ha massimi relativi
(D) ha in x = 2 il suo unico massimo relativo e non ha minimi relativi
(E) ha in x = 1 il suo unico minimo relativo e non ha massimi relativi
(F) ha in x = 1 il suo unico massimo relativo e non ha minimi relativi
—————————————————————————
14) La retta tangente al grafico della funzione f(r) = 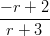 in r = 1 è
in r = 1 è
|
(A) (B) - (C) (D) (E) - (F) |
—————————————————————————
15) La funzione f(t) = 3t2 - 24 ln (16t), definita per t > 0, ha
|
(A) un massimo relativo in (B) un minimo relativo in 8 (C) un minimo relativo in (D) un massimo relativo in 8 (E) un minimo relativo in 2 (F) un massimo relativo in 2 |
—————————————————————————
16) Data la funzione g(z) = 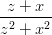 , dove x è un parametro. Il valore della derivata, nel punto z = -x
è
, dove x è un parametro. Il valore della derivata, nel punto z = -x
è
|
(A) - (B) 0 (C) (D) (E) (F) +∞ (G) - (H) - |
—————————————————————————
17) La funzione |x2 - 2x + 1|
(A) ha solo un massimo relativo e nessun minimo
(B) ha due minimi relativi ed un massimo relativo
(C) ha un massimo e un minimo relativi
(D) ha solo un minimo relativo e nessun massimo
(E) ha due massimi relativi e nessun minimo
—————————————————————————
18) La retta tangente al grafico della funzione f(x) = 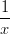 nel punto x = -1 è
nel punto x = -1 è
|
(A) -1 + (x - 1) (B) -1 + (x + 1) (C) -1 - (x + 1) (D) 1 + (x - 1) (E) 1 - (x + 1) (F) 1 + (x + 1) (G) -1 - (x - 1) (H) 1 - (x - 1) |
—————————————————————————
19) La funzione f(x) = 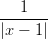
(A) è crescente in (-∞, 1) e decrescente in (1, +∞)
(B) è decrescente in (-∞, 0) e (1, +∞), crescente in (0, 1)
(C) è decrescente in (-∞, 1) e crescente in (1, +∞)
(D) è crescente in (-∞, 0) e (1, +∞), decrescente in (0, 1)
—————————————————————————
20) La retta tangente al grafico della funzione f(x) = 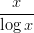 nel punto x = e è:
nel punto x = e è:
|
(A) y = e (B) y = 0 (C) y = 1 (D) y = e + x (E) y = x (F) y = 1 + x |
—————————————————————————
21) La funzione f(x) = ex2-2x+1
(A) ha solo un minimo relativo e nessun massimo
(B) ha solo un massimo relativo e nessun minimo
(C) ha due minimi ed un massimo relativi
(D) ha due massimi ed un minimo relativi
(E) ha un massimo e un minimo relativo
(F) nessuna delle altre
—————————————————————————
22) La derivata della funzione f(s) = 4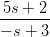 in s = 1 è
in s = 1 è
|
(A) 13 (B) 34 (C) 26 (D) 17 |
—————————————————————————
23) La funzione f(x) = -6e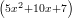
(A) non ha né un massimo né un minimo in x = -1
(B) ha un massimo relativo in x = -1
(C) ha un minimo relativo in x = -1
—————————————————————————
24) La funzione f(r) = -2e-2r-2 è crescente ∀r 
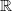
|
(A) vero (B) falso |
—————————————————————————
25) La funzione f(q) = 14q6 + 15q8 è crescente ∀q 
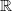
|
(A) vero (B) falso |
—————————————————————————
26) Sia f(x) = 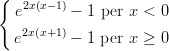
(A) La funzione f ha un massimo ed un minimo relativi
(B) La funzione f ha un solo minimo relativo, e non ha massimi relativi
(C) La funzione f ha un solo massimo relativo, e non ha minimi relativi
(D) La funzione f ha due massimi relativi ed un minimo relativo
(E) La funzione f ha due minini relativi ed un massimo relativo
(F) La funzione f non ha né massimi né minimi relativi
—————————————————————————
27) Nell’intervallo (-2, - 1), la funzione f(x) = ln(2x2 + 6x + 6) ha un mimino relativo in
-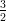
|
(A) falso (B) vero |
—————————————————————————
28) Sia f(x) = 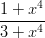 . Il punto x = 0 è
. Il punto x = 0 è
|
(A) un punto di minimo locale (B) un punto di massimo locale |
—————————————————————————
29) Sia f(x) = 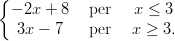
Il punto x = 3
(A) è un punto di massimo locale
(B) è un punto di minimo locale
(C) non è né un punto di massimo locale né un punto di minimo locale
—————————————————————————
30) Sia f(x) = e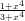 . Il punto x = 0 è
. Il punto x = 0 è
|
(A) un punto di minimo locale (B) un punto di massimo locale |
—————————————————————————
31) Sia f(x) = 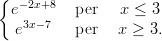
Il punto x = 3
(A) non è né un punto di massimo locale né un punto di minimo locale
(B) è un punto di massimo locale
(C) è un punto di minimo locale
—————————————————————————
32) La funzione ex2+9x+20 ha uno ed un solo massimo relativo
|
(A) falso (B) vero |
—————————————————————————
33) La funzione e-|x2+9x+20|
(A) ha un minimo relativo in -5, un minimo relativo in - , un massimo relativo in -4
, un massimo relativo in -4
(B) ha un minimo relativo in -5, un massimo relativo in -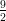 , un minimo relativo in -4
, un minimo relativo in -4
(C) ha un massimo relativo in -5, un massimo relativo in -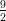 , un massimo relativo in
-4
, un massimo relativo in
-4
(D) ha un massimo relativo in -5, un minimo relativo in - , un massimo relativo in -4
, un massimo relativo in -4
(E) ha un minimo relativo in -5, un minimo relativo in -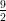 , un minimo relativo in -4
, un minimo relativo in -4
(F) ha un minimo relativo in -5, un massimo relativo in - , un massimo relativo in -4
, un massimo relativo in -4
(G) ha un massimo relativo in -5, un massimo relativo in - , un minimo relativo in -4
, un minimo relativo in -4
(H) ha un massimo relativo in -5, un minimo relativo in -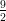 , un minimo relativo in -4
, un minimo relativo in -4
—————————————————————————
34) Sia v(s) = 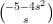 un vettore le cui coordinate dipendono dal parametro reale s
un vettore le cui coordinate dipendono dal parametro reale s 
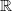 , e sia
w =
, e sia
w = 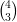 . Il prodotto scalare v(s) ⋅ w, come funzione di s, ha un minimo relativo.
. Il prodotto scalare v(s) ⋅ w, come funzione di s, ha un minimo relativo.
|
(A) vero (B) falso |
—————————————————————————
35) Si consideri la funzione f(r) = 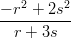 , dove s è un parametro reale non nullo.
, dove s è un parametro reale non nullo. 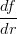 (r), calcolata
nel punto r = s vale:
(r), calcolata
nel punto r = s vale:
(A) -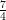 s
s
(B) -
(C) -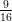
(D) -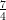
(E) - s
s
(F) nessuna delle altre
(G) -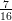
—————————————————————————
36) La funzione
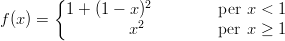
(A) ha massimo assoluto e non ha minimo assoluto
(B) ha minimo assoluto e non ha massimo assoluto
(C) non ha né minimo assoluto né massimo assoluto
(D) ha massimo e minimo assoluti
—————————————————————————
37) La funzione f(v) = |- v2 - 5v - 6|è
(A) decrescente per v > - e crescente per v < -
e crescente per v < -
(B) decrescente per -3 < v < -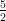 , crescente per v < -3 e v > -
, crescente per v < -3 e v > -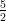
(C) decrescente per v < -3 e - < v < -2, crescente per -3 < v < -
< v < -2, crescente per -3 < v < - e v > -2
e v > -2
(D) decrescente per v < - e crescente per v > -
e crescente per v > -
(E) decrescente per -3 < v < -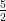 e v > -3, crescente per v < -3 e -
e v > -3, crescente per v < -3 e -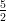 < v < -2
< v < -2
(F) decrescente per v < -3 e v > - , crescente per -3 < v < -
, crescente per -3 < v < -
—————————————————————————
38) Sia f(r) = e-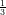 r3+r, con r
r3+r, con r 
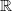 . Essa ha:
. Essa ha:
(A) minimo locale in r = 1, massimo locale in r = -1 e non ha massimi e minimi assoluti
(B) minimo locale in r = -1, massimo assoluto in r = 1 e non ha minimo assoluto
(C) massimo assoluto in 0 e non ha minimi né relativi né assoluti
(D) minimo assoluto in r = 1, massimo locale in r = -1 e non ha massimo assoluto
(E) minimo locale in r = 1, massimo assoluto in r = -1 e non ha minimo assoluto
(F) minimo locale in r = -1, massimo locale in r = 1 e non ha massimi e minimi assoluti
(G) minimo assoluto in r = -1, massimo locale in r = 1 e non ha massimo assoluto
(H) minimo assoluto in 0 e non ha massimi né relativi né assoluti
—————————————————————————
39) Sia f(x) = 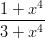 . Il punto x = 0 è
. Il punto x = 0 è
|
(A) un punto di massimo locale (B) un punto di minimo locale |
—————————————————————————
40) La funzione f(r) = -2e-2r-2 è crescente ∀r 
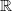
|
(A) falso (B) vero |
—————————————————————————
41) La funzione f(x) = |2x2 - 2|
(A) ha minimi relativi in x = -1 e x = 1, e massimo relativo in x = 0
(B) ha massimi relativi in x = -1 e x = 1, e minimo relativo in x = 0
(C) ha massimo relativo in x = 0 e non ha minimi relativi
(D) ha minimo relativo in x = 0 e non ha massimi relativi
—————————————————————————
42) Sia f(x) = 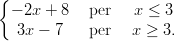 Il punto x = 3
Il punto x = 3
(A) non è né un punto di massimo locale né un punto di minimo locale
(B) è un punto di massimo locale
(C) è un punto di minimo locale
—————————————————————————
43) La funzione f(x) = e-x2+2x+3
|
(A) ha un minimo locale (B) ha un massimo locale |
—————————————————————————
44) La funzione f(x) = -2e-3x + 4e5x
|
(A) è sempre crescente (B) è sempre decrescente |
—————————————————————————
45) Sia
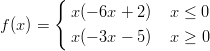
(A) ha due minimi locali
(B) nessuna delle altre
(C) ha un minimo locale
(D) ha due massimi locali
(E) ha un massimo locale
—————————————————————————
46) La funzione f(x) = 2x3 + 3x2 + 4x - 12
|
(A) ha un massimo e un minimo locali (B) ha un massimo locale e nessun minimo (C) non ha né massimi né minimi locali (D) ha un minimo locale e nessun massimo |
—————————————————————————
47) La funzione f(x) = -2e-3x + 4e5x ha derivata
|
(A) negativa per ogni x (B) positiva per ogni x |
—————————————————————————
48) Sia
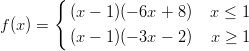
(A) ha un massimo locale
(B) ha due massimi locali
(C) ha un minimo locale
(D) ha un massimo e un minimo locali
(E) ha due minimi locali
—————————————————————————
49) Un razzo percorre lo spazio in funzione del tempo con la seguente legge: s(t) = 18t2 - 3t3. Quant’è la velocità massima che raggiunge nell’intervallo di tempo [0, 3]?
|
(A) 27 (B) 48 (C) 96 (D) 36 |
—————————————————————————
50) Sia f(x) = 3 log(4 + 5x). La sua derivata in x = 1 è
|
(A) (B) 3 log 9 (C) (D) 3 log 5 |
—————————————————————————
51) Sia f(x) = 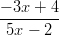 . La sua derivata in x = 0 è
. La sua derivata in x = 0 è
|
(A) 7 (B) - (C) -13 (D) (E) -2 (F) 0 |
—————————————————————————
52) Sia
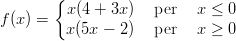
|
(A) non ha né massimi né minimi locali (B) ha due minimi e un massimo locali (C) ha due massimi locali e nessun minimo (D) ha due massimi e un minimo locali (E) ha due minimi locali e nessun massimo (F) ha un massimo e un minimo locali |
—————————————————————————
53) La funzione f(x) = e14x3+12x2+15x-12
(A) non ha né massimi né minimi locali
(B) ha un massimo locale e nessun minimo locale
(C) ha un massimo e un minimo locali
(D) ha un minimo locale e nessun massimo locale
—————————————————————————
54) Sia f(x) = 3 log(4 + 5x). La sua derivata in x = 0 è
|
(A) 3 log 5 (B) (C) (D) 3 log 9 |
—————————————————————————
55) Sia f(x) = 18x2 - 3x3. Qual è il valore massimo della funzione derivata f′(x) nell’intervallo [0, 3]?
|
(A) 96 (B) 48 (C) 27 (D) 36 |
—————————————————————————
56) L’intervallo di crescenza della funzione f(x) = log(7x2 - 4x + 3) è:
(A) (-∞, + ∞)
(B) (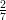 , +∞)
, +∞)
(C) (-∞, log 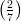 )
)
(D) (-∞, 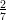 )
)
(E) (log 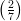 , + ∞)
, + ∞)
—————————————————————————
57) Sia f(x) = 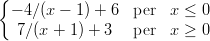
|
(A) non ha né massimi né minimi (B) ha un massimo e nessun minimo (C) ha un minimo e nessun massimo (D) ha un massimo e un minimo |
—————————————————————————
58) Sia f(x) = 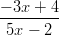 . L’affermazione
. L’affermazione
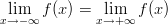
|
(A) è vera (B) è falsa |
—————————————————————————
59) La funzione
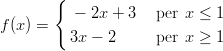
(A) ha un minimo e non ha massimi
(B) ha un massimo e non ha minimi
(C) non ha né massimi né minimi
—————————————————————————
60) Si consideri la funzione f(x) = x2 - 2x- 8, definita nell’intervallo ![[0, 3]](esercizi357x.png) . Il suo massimo assoluto è
nel punto
. Il suo massimo assoluto è
nel punto
|
(A) 0 (B) 1 (C) 3 |
—————————————————————————
61) L’intervallo di crescenza della funzione f(x) = (7x2 - 4x + 3)3 è:
(A) (-∞, 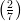 3)
3)
(B) (-∞, 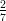 )
)
(C) (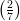 3, + ∞)
3, + ∞)
(D) (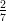 , +∞)
, +∞)
(E) (-∞, + ∞)
—————————————————————————
62) Sia f(x) = xe-2x2+7x. La sua derivata in x = 1 è
(A) 1 + 3e5
(B) 3e3
(C) 3e5
(D) 4e5
(E) 4e3
(F) e3
(G) 1 + 3e3
—————————————————————————
63) Sia f(x) = 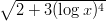 . La derivata di f nel punto x = e vale:
. La derivata di f nel punto x = e vale:
|
(A) 2 (B) (C) 6 (D) 2 (E) (F) 2 (G) (H) 6 |
—————————————————————————
64) Sia f(x) = 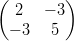
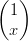 ⋅
⋅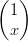 . (È un prodotto riga-colonna tra la matrice e il vettore, il cui
risultato va moltiplicato scalarmente per il secondo vettore). Il suo unico minimo si ottiene
per
. (È un prodotto riga-colonna tra la matrice e il vettore, il cui
risultato va moltiplicato scalarmente per il secondo vettore). Il suo unico minimo si ottiene
per
|
(A) -3∕5 (B) -6∕5 (C) -2∕5 (D) 6∕5 (E) -3∕2 (F) 3∕5 (G) 2∕5 (H) 3∕2 |
—————————————————————————
65) Un razzo si allontana dalla Terra con la seguente legge oraria (cioè spazio in funzione del tempo):
s(t) = 6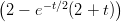 . Quant’è la velocità massima che raggiunge per t ≥ 0?
. Quant’è la velocità massima che raggiunge per t ≥ 0?
|
(A) 12 (B) 3∕e (C) 18 (D) 6∕e (E) 0 (F) 2∕e |
—————————————————————————
66) Sia f(x) = 4![[log(e + 5x)]](esercizi376x.png) 2. La sua derivata nel punto x = 0 vale:
2. La sua derivata nel punto x = 0 vale:
|
(A) 16e (B) 8 (C) 20∕e (D) 40∕e (E) 80 (F) 4e |
—————————————————————————
|
1 C 2 B 3 A 4 B 5 A 6 B 7 A 8 E 9 C 10 I 11 F 12 E 13 B 14 C 15 E 16 E 17 D 18 C 19 A 20 A 21 A 22 D 23 B 24 A 25 B 26 B 27 B 28 A 29 B 30 A 31 C 32 A 33 D 34 B 35 C 36 B 37 C 38 F 39 B 40 B 41 A 42 C 43 B 44 A 45 E 46 C 47 B 48 A 49 D 50 C 51 B 52 B 53 A 54 C 55 D 56 B 57 B 58 A 59 A 60 C 61 D 62 D 63 C 64 F 65 D 66 D |
1) Il valore dell’integrale ∫
0πx cos 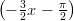 dx è
dx è
|
(A) (B) (C) - |
—————————————————————————
2) La funzione f(x) = ∫ 0x(sin s - 1)3ds
(A) per ogni x > 0 cresce
(B) per ogni x  (0,
(0,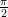 ) decresce
) decresce
(C) per ogni x  (
(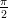 ,π) cresce
,π) cresce
—————————————————————————
3) Il valore dell’integrale ∫
0+∞dxxe2-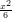 è esprimibile come ze2,
è esprimibile come ze2,
con z opportuno numero reale. Determinare il valore di z (procedere per sostituizione).
|
(A) 3 (B) 6 (C) 8 (D) 7 (E) 4 |
—————————————————————————
4) La primitiva della funzione e-2x(8x - 12) è esprimibile come e-2x(-4x + z) + c,
con z opportuno numero reale e c costante arbitraria. Determinare il valore di z ( procedere integrando per parti).
(Si ricordi che ∫
eax =  eax.)
eax.)
|
(A) -10 (B) -22 (C) -14 (D) 4 (E) -3 |
—————————————————————————
5) Calcolare la media della funzione 2 + 6x2 nell’intervallo [1, 3]
|
(A) 29 (B) 8 (C) 28 (D) 0 (E) 55 |
—————————————————————————
6) ∫
01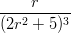 dr =
dr =
(A) 
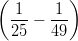
(B)  ⋅
⋅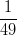
(C) 
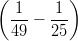
(D) 
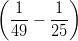
(E) 
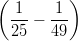
—————————————————————————
7) ∫ 0+∞(13r + 7)e-2r+2dr =
|
(A) (B) +∞ (C) (D) (E) (F) -∞ |
—————————————————————————
8) La media della funzione 4x3 nell’intevallo [-3, 2] è
|
(A) -65 (B) 81 (C) -13 (D) 16 |
—————————————————————————
9) L’integrale ∫
84+∞dx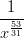 è
è
|
(A) finito (B) infinito |
—————————————————————————
10) L’integrale ∫
1+∞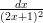 vale:
vale:
(A) 
(B) -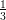
(C) 0
(D) +∞
(E) -∞
(F) 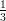
(G) -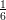
—————————————————————————
11) Calcolare, procedendo per sostituzione, l’integrale ∫ -4+∞2xe-x2+2dx
(A) 2e-14
(B) 0
(C) -e-14
(D) -2e-14
(E) -∞
(F) +∞
(G) e-14
—————————————————————————
12) La funzione f(x) = ∫
-∞xe-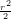
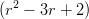 dr, con x
dr, con x 
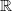
(A) è crescente in tutto 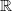
(B) decresce in (-∞, 1) e (2, +∞), e cresce in (1, 2)
(C) cresce negli intervalli in cui -x3 + 3x2 + 2 > 0
(D) cresce in (-∞, 1) e (2, +∞), e decresce in (1, 2)
(E) è decrescente in tutto 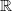
—————————————————————————
13) Calcolare ∫
0+∞x3e-2x dx. Potete utilizzare il fatto che la primitiva di xke-x, per
k ≥ 1 intero, è -e-x(xk + kxk-1 + k(k - 1)xk-2 + k(k - 1)(k - 2)xk-3 +  + k!), dove
k! = k(k - 1)(k - 2)(k - 3) ⋅…3 ⋅ 2 ⋅ 1.
+ k!), dove
k! = k(k - 1)(k - 2)(k - 3) ⋅…3 ⋅ 2 ⋅ 1.
|
(A) (B) -6 (C) (D) - (E) - (F) 6 |
—————————————————————————
14) Calcolare per sostituzione ∫
01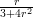 dr (utilizzare come nuova variabile il denominatore)
dr (utilizzare come nuova variabile il denominatore)
(A) 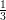 ln
ln 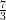
(B) 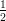 ln
ln 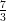
(C) 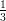 ln
ln 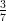
(D) 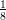 ln
ln 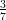
(E) 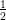 ln
ln 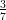
(F) 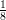 ln
ln 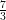
(G)  ln
ln 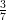
(H) 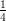 ln
ln 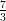
—————————————————————————
15) Calcolare ∫
01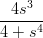 ds (procedere per sostituzione, usando il denominatore come nuova
variabile)
ds (procedere per sostituzione, usando il denominatore come nuova
variabile)
(A) 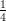 log
log 
(B) 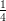 log
log 
(C) log 
(D) log 
(E) +∞
(F) 0
(G) -∞
—————————————————————————
16) La funzione 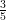 x
x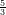 è una primitiva della funzione x
è una primitiva della funzione x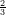
|
(A) vero (B) falso |
—————————————————————————
17) La densità ρ dell’aria in funzione della quota h dal livello del mare segue la legge ρ(h) = 2e-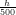 ,
con h in centimetri e ρ in milligrammi al centimetro cubo. Quant’è la massa in milligrammi di un
cilindro di aria con la base a livello del mare, con area di base di un centimetro quadro, e di altezza
1000 centrimetri?
,
con h in centimetri e ρ in milligrammi al centimetro cubo. Quant’è la massa in milligrammi di un
cilindro di aria con la base a livello del mare, con area di base di un centimetro quadro, e di altezza
1000 centrimetri?
(A) 1000e2
(B) 2e2
(C) 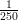 e-2
e-2
(D) 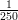 e2
e2
(E) 2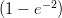
(F) 1000e-2
(G) 2e-2
(H) 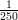
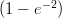
(I) 1000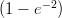
(J) 1000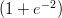
(K) 2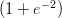
(L) 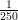
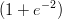
—————————————————————————
18) Il tasso istantaneo di crescita di una popolazione, indicato con α, varia nel tempo con la legge α(t) = 3 + t + t2. Supponendo che al tempo t = 0 la numerosità è 1000, al tempo t = 2 quant’è la numerosità?
|
(A) 1000 + (B) 9 ⋅ 1000 (C) (D) 9 + 1000 |
—————————————————————————
19) La funzione 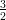 e
e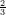 x è una primitiva della funzione e
x è una primitiva della funzione e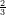 x
x
|
(A) vero (B) falso |
—————————————————————————
20) Nel fondo di un fiume vive un organismo unicellulare sensibile alla salinità dell’acqua. È noto che
la densità m della numerosità di tale organismo, in funzione della distanza dalla foce x,
segue la legge m(x) = 2e-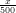 , con x in metri e m in milioni di individui al metro. Quant’è
il numero, in milioni di individui, in un tratto di fiume lungo 1000 metri, a partire dalla
foce?
, con x in metri e m in milioni di individui al metro. Quant’è
il numero, in milioni di individui, in un tratto di fiume lungo 1000 metri, a partire dalla
foce?
(A) 2
(B) 2e2
(C) 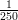
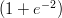
(D) 1000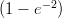
(E) 1000e-2
(F) 1000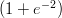
(G) 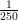 e2
e2
(H) 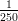
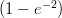
(I) 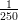 e-2
e-2
(J) 1000e2
(K) 2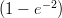
(L) 2e-2
—————————————————————————
21) La numerosità di una popolazione si evolve secondo la legge N(t) = 1000e-t2+6t-8, per 0 ≤ t ≤ 1. Quant’è il massimo del “tasso istantaneo di crescita per unità di popolazione”, nell’intervallo assegnato?
|
(A) 1000e1 (B) 1000e-8 (C) 1000e-3 (D) 2 (E) -4 (F) 6 |
—————————————————————————
22) La funzione f(x) = ex2+x-3 è una primitiva di g(x) = (2x + 1)ex2+x-3
|
(A) vero (B) falso |
—————————————————————————
23) Nell’intervallo di tempo [0, 3], un autoveicolo segue la legge oraria s(t) = 2t(6 - t) (t è il tempo in minuti, s lo spazio percorso in kilometri). Si supponga che il consumo istantaneo di carburante sia di 4 + 5v(t) millilitri al minuto, dove v(t) è la velocitá al tempo t, espressa in kilometri al minuto. Quanti millilitri di carburante vengono consumati nell’intervallo di tempo [0, 3]?
|
(A) 9 (B) 66 (C) 84 (D) 6 (E) 12 (F) 102 (G) 48 (H) 19 |
—————————————————————————
24) 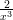 è una primitiva di
è una primitiva di 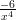
|
(A) falso (B) vero |
—————————————————————————
25) Quale delle seguenti funzioni è una primitiva di 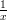 ?
?
|
(A) log (1 + x) (B) log (2x) (C) log x2 (D) nessuna delle altre |
—————————————————————————
26) Il tasso istantaneo di crescita della numerosità di una popolazione varia nel tempo con la legge r(t) = 4t, con il tempo misurato in giorni. Ogni individuo consuma 6 grammi di cibo al giorno. Quanti grammi di cibo sono stati consumati dalla popolazione nell’intervallo di tempo [0, 10], sapendo che al tempo 0 la numerositá era di 1000 individui?
(A) 64000
(B) 5000
(C) 4200
(D) 1200
(E) 6240
(F) 4000
(G) 7200
—————————————————————————
27) La funzione e-x2-9x-20 è una primitiva di -(2x + 9)e-x2-9x-20
|
(A) vero (B) falso |
—————————————————————————
28) Lungo il fondo di un fiume è depositata una sostanza inquinante. La funzione m(x) = 2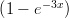 esprime la massa di inquinante compresa nel tratto tra la sorgente e il kilometro x, misurato dalla
sorgente. La massa di inquinante presente nel tratto 2 < x < 4 è
esprime la massa di inquinante compresa nel tratto tra la sorgente e il kilometro x, misurato dalla
sorgente. La massa di inquinante presente nel tratto 2 < x < 4 è
(A) 2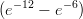
(B) 4 + 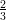
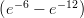
(C) 6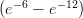
(D) 2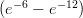
(E) 6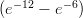
(F) 4 + 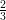
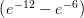
—————————————————————————
29) La numerosità di una popolazione ha un tasso istantaneo di crescita al tempo t espresso da r(t) = 200e2t. Al tempo t = 0 la numerosità è n(0) = 100. Quant’è la numerosità al tempo t = 4 ?
(A) 100 + 800e8
(B) 100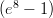
(C) 200e8
(D) 100 + 200e8
(E) 800e8
(F) 100 + 800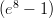
(G) 100e8
—————————————————————————
30) ∫
0
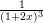 dx vale
dx vale
|
(A) (B) - (C) (D) - (E) (F) - |
—————————————————————————
31) Nella città di Prato, dalle 20 alle 8 il traffico produce benzene al ritmo di 5Kg al giorno, dalle 8 alle 20 al ritmo di 25Kg al giorno. Quanti kilogrammi di benzene vengono prodotti da mezzanotte a mezzogiorno?
(A) 
(B) 25
(C) 5
(D) 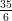
(E) 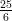
(F) 15
(G) 140
—————————————————————————
32) Sul fondo di un fiume si è depositato un inquinante. È noto che la massa di inquinante
nel tratto a < x < b è data da  μg, dove x è la distanza dalla fonte, misurata
in metri. La densità di inquinante in μg al metro, nel punto di distanza x dalla sorgente
è
μg, dove x è la distanza dalla fonte, misurata
in metri. La densità di inquinante in μg al metro, nel punto di distanza x dalla sorgente
è
|
(A) (B) (C) (D) (E) ln (1 + x) - ln(1 + a) (F) ln (1 + x) |
—————————————————————————
33) ∫ 13dy ∫ 12dx (2x - 7)(2y - 9) =
|
(A) 24 (B) 504 (C) 36 (D) 40 (E) 480 |
—————————————————————————
34) La funzione f(x) = (2x + 3)e2x è una primitiva di g(x) = (4x + 8)e2x?
|
(A) no (B) si |
—————————————————————————
35) ∫ 382|x - 5|dx =
|
(A) 13 (B) 5 (C) -5 (D) 55 |
—————————————————————————
36) In opportune unità di misura, la massa di atmosfera sopra un’area di un metro quadro, compresa tra il suolo e la quota h è 20(1 - e-h∕4). La densità di massa alla quota h = 12 è
(A) 20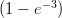
(B) 80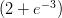
(C) 5e-3
—————————————————————————
37) La funzione 2e3x è una primitiva della funzione 6e3x?
|
(A) no (B) si |
—————————————————————————
38) ∫ 1∕27∕2|2x - 3|dx =
|
(A) 3 (B) 5∕2 (C) -3∕2 (D) 5 (E) -3 (F) -5 (G) -5∕2 (H) 3∕2 |
—————————————————————————
39) ∫
-11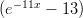 =
=
(A) 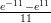 - 26
- 26
(B) 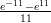 - 13
- 13
(C) 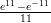
(D) 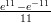 - 26
- 26
(E) 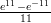 - 13
- 13
(F) 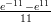
(G) -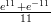
(H) -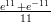 - 13
- 13
(I) -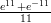 - 26
- 26
—————————————————————————
40) Viene misurata la massa di carbonio presente in una ’carota’ di uno scavo geologico. La massa tra il suolo e la profondità h è m(h) = 18h2 - 3h3. Si calcoli la funzione ’densità lineare di massa’ ρ(h), e si dica qual è il valore massimo che ρ(x) assume nell’intervallo [0, 3] (massimo assoluto).
|
(A) 48 (B) 96 (C) 27 (D) 36 |
—————————————————————————
41) Un ciclista percorre un circuito in un minuto. La sua velocità in funzione del tempo è v(t) = 500 + 100 cos(2πt) metri al minuto. Ricordando che ∫ dx cos(x) = sin(x), si determini la lunghezza del circuito.
|
(A) circa 515.915 metri (B) 500 metri (C) circa 484.085 metri (D) 600 metri |
—————————————————————————
42) ∫ 1∕27∕2(1 + |2x - 3|) dx =
|
(A) 11∕2 (B) 0 (C) 1∕2 (D) -2 (E) 9∕2 (F) 3∕2 (G) 8 (H) 6 |
—————————————————————————
43) Sia
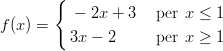
|
(A) 9∕2 (B) 1∕2 (C) -1∕2 (D) 2 (E) 4 (F) 5 |
—————————————————————————
44) Un conducente di un veicolo inizia a frenare a t = 0, nell’istante in cui vede un ostacolo davanti a sé a distanza 2. La sua velocità durante la frenata è data da v(t) = 3 - 2t. La frenata non gli permette di evitare l’ostacolo. Con che velocità lo urta?
|
(A) 2 (B) 3 (C) 9 / 2 (D) 1 |
—————————————————————————
45) ∫ 01dx∫ 02dy(2x + 3y) =
|
(A) 5 (B) 10 (C) 7 (D) 6 (E) 2 (F) 4 (G) 8 (H) 3 |
—————————————————————————
46) Per un referendum, nel primo giorno i seggi restano aperti dalle 8 alle 22. Il flusso di elettori ai seggi segue la seguente legge
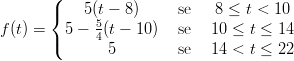
|
(A) 21:30 (B) 21 (C) 19:30 (D) 17:30 (E) mai (F) 18 (G) 20 (H) 17 (I) 16 (J) 20:30 (K) 15 (L) 18:30 (M) 22 (N) 15:30 (O) 16:30 (P) 19 |
—————————————————————————
47) Nell’intervallo di tempo [0, 2], un razzo si allontana dalla Terra con la seguente legge oraria (cioè spazio in funzione del tempo): s(t) = 3t + 4t2. Quant’è la velocità media nell’intervallo di tempo [0, 2]?
|
(A) 104∕3 (B) 11 (C) 19∕2 (D) 19 |
—————————————————————————
48) ∫ 02dy ∫ 01dx(2x + 3y) =
|
(A) 7 (B) 8 (C) 2 (D) 6 (E) 4 (F) 5 (G) 3 (H) 10 |
—————————————————————————
49) Sia
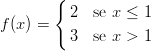
|
(A) -1∕3 (B) 2 (C) 5∕3 (D) 2∕3 (E) 5∕2 (F) 3∕2 |
—————————————————————————
50) ∫ 01dx∫ 23dy xe2y è uguale a
(A) 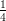 e
e
(B) 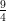 e6 - e4
e6 - e4
(C) 3e6 - 2e4
(D) 
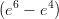
(E) 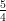 (e - 1)
(e - 1)
—————————————————————————
51) ∫ 01dx∫ 23dy ye2x è uguale a
(A) 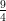 e6 - e4
e6 - e4
(B) 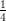

(C)  (e - 1)
(e - 1)
(D)  e
e
(E) 3e6 - 2e4
—————————————————————————
52) ∫ 12dx∫ 12dy xexy è uguale a
|
(A) - (B) (C) (D) (E) (F) |
—————————————————————————
|
1 A 2 B 3 A 4 D 5 C 6 E 7 D 8 C 9 A 10 A 11 G 12 D 13 C 14 F 15 C 16 A 17 I 18 A 19 A 20 D 21 F 22 A 23 F 24 B 25 B 26 A 27 A 28 D 29 G 30 E 31 D 32 D 33 D 34 B 35 A 36 C 37 B 38 D 39 D 40 D 41 B 42 G 43 A 44 D 45 G 46 G 47 B 48 B 49 C 50 D 51 C 52 F |
1) Se f = f(x,y) è una funzione di due variabili, il gradiente nel punto (x0,y0) è
|
(A) un vettore bidimensionale (B) un numero reale (C) una funzione (D) un numero intero (E) una retta (F) una curva |
—————————————————————————
2) Il gradiente in un punto (x0,y0) di una funzione di due variabili f(x,y) è:
(A) ortogonale alla curva di livello che passa per (x0,y0)
(B) tangente a tutte le curve di livello
(C) tangente alla curva di livello che passa per (x0,y0)
(D) ortogonale a tutte le curve di livello
—————————————————————————
3) Data una funzione di due variabili f(x,y). In un punto di massimo relativo il gradiente è
(A) un vettore che punta verso l’alto
(B) un numero negativo
(C) un numero positivo
(D) il numero 0
(E) un vettore con tutte le componenti nulle
(F) un vettore che punta verso il massimo
(G) un vettore che punta verso il basso
—————————————————————————
4) Per una funzione di due variabili f(x,y), la curva di livello f = c è
(A) l’insieme dei punti (x,y) tali che f(x,y) = c
(B) un numero
(C) una regione in cui la funzione ha il grafico parallelo al piano (x,y)
(D) un vettore che punta nella direzione di massima pendenza
—————————————————————————
5) Se f = f(x,y) è una funzione di due variabili, il gradiente nel punto (x0,y0) è
|
(A) un numero reale (B) una curva (C) una retta (D) un vettore bidimensionale (E) una funzione (F) un numero intero |
—————————————————————————
6) Il gradiente in un punto (x0,y0) di una funzione di due variabili f(x,y) è:
(A) ortogonale al grafico della funzione
(B) tangente a tutte le curve di livello
(C) ortogonale alla curva di livello che passa per (x0,y0)
(D) tangente al grafico della funzione
(E) ortogonale a tutte le curve di livello
(F) tangente alla curva di livello che passa per (x0,y0)
(G) ortogonale al piano (x,y)
—————————————————————————
7) Per una funzione di due variabili f(x,y), la curva di livello f = c è
(A) l’insieme dei punti (x,y) tali che f(x,y) = c
(B) un punto (x,y) tale che f(x,y) = c
(C) un vettore che punta nella direzione di massima pendenza
(D) una regione in cui la funzione ha il grafico parallelo al piano (x,y)
(E) un numero
—————————————————————————
8) Sia f(x,y,z) = xyz. Il gradiente di f nel punto (1, 2, 1) è
(A) 3
(B) 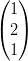
(C) 2
(D) 5
(E) 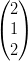
—————————————————————————
9) La funzione f(x,y) = x2 + y2 ha un minimo di (x,y) = (0, 0) perché
(A) ∂x f = 0 soltanto se x = 0
(B) f ≥ 0 per ogni x e y, ed è uguale a 0 solo per (x,y) = (0, 0)
(C) il gradiente di f è il vettore nullo in (x,y) = (0, 0)
(D) ∂x f = 0 e ∂yf = 0 soltanto in (x,y) = (0, 0)
—————————————————————————
10) Sulla vetta di una montagna il gradiente della funzione quota sul livello del mare è
(A) un vettore che punta verso il basso
(B) un vettore che punta verso l’alto
(C) il vettore nullo
(D) un vettore orizzonatale che punta verso la valle più vicina
—————————————————————————
11) Sia f(x,y) = ex2+y2. Il gradiente di f è
|
(A) 2ex2 +y2(x + y) (B) 2ex2 +y2 (C) e |
—————————————————————————
12) Si consideri la funzione p(x,y) =profondità del fondale marino. La curva di livello p(x,y) = 0 rappresenta
(A) la linea di costa
(B) un punto in cui il fondale è piatto
(C) l’insieme dei punti in cui il fondale è piatto
—————————————————————————
13) Se f = f(x,y) è una funzione di due variabili, il gradiente nel punto (x0,y0) è
|
(A) un numero reale (B) un vettore bidimensionale (C) una retta (D) una funzione (E) una curva (F) un numero intero |
—————————————————————————
14) Sia f(x,y) = ex2+y2. Il gradiente di f è
|
(A) 2ex2 +y2(x + y) (B) 2ex2 +y2 (C) e |
—————————————————————————
15) Si consideri la funzione p(x,y) =profondità del fondale marino. La curva di livello p(x,y) = 0 rappresenta
(A) la linea di costa
(B) un punto in cui il fondale è piatto
(C) l’insieme dei punti in cui il fondale è piatto
—————————————————————————
16) Sia f(x,y) = (x - xy + 2y)2 + 3. Il punto (2, 1) può essere di minimo locale?
|
(A) si (B) no |
—————————————————————————
17) Sia f(x,y) = (2x2 + 6x + 2)(5y2 + 3y + 5). Il gradiente nel punto (0,0) è il vettore:
|
(A) (6, 5) (B) (2, 5) (C) (10, 13) (D) (6, 3) (E) (30, 6) |
—————————————————————————
18) Sia f(x,y) = (x - xy + 2y)2 + 3. Il gradiente nel punto (2, 1) è il vettore nullo?
|
(A) no (B) si |
—————————————————————————
19) Sia f(x,y) = -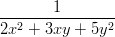 . Il gradiente nel punto (1, 1) è:
. Il gradiente nel punto (1, 1) è:
(A) 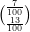
(B) 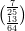
(C) 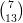
—————————————————————————
20) Sia v = 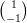 , sia f(x,y) = (3x + 4)(5y + 2), e sia w il gradiente di f nel punto (0, 0). Il prodotto
scalare v ⋅ w vale
, sia f(x,y) = (3x + 4)(5y + 2), e sia w il gradiente di f nel punto (0, 0). Il prodotto
scalare v ⋅ w vale
|
(A) -14 (B) 8 (C) 26 (D) -2 |
—————————————————————————
21) Sia f(x,y) = 4x2 - 3y2 + 8xy - 9x + 4y + 7. Il gradiente di f è nullo in
|
(A) un solo punto (B) infiniti punti (C) nessun punto |
—————————————————————————
22) Sia f(x,y) = 4x2 + 12xy + 9y2. Il suo gradiente è nullo
|
(A) in un solo punto (B) in due punti (C) in infiniti punti (D) in nessun punto |
—————————————————————————
23) Sia V (x,y) una primitiva del differenziale esatto
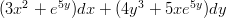
|
(A) 10 - 2e5 + e10 (B) -8 + 2e5 - e10 (C) 10 - e5 + 2e10 (D) 10 + e5 - 2e10 (E) 24 - e5 + 2e10 (F) 24 + e5 - 2e10 (G) 10 + 2e5 - e10 (H) -8 - 2e5 + e10 |
—————————————————————————
24) Sia f(x,y) = x2y3e5x+5y. In quali punti (x,y), con x≠0 e y≠0, il suo gradiente è nullo?
|
(A) (-5∕2, - 5∕3) (B) (-2, - 3) (C) (-1∕2, - 1∕3) (D) (-1∕5, - 1∕5) (E) (-2∕5, - 3∕5) (F) (-5, - 5) |
—————————————————————————
25) Il differenziale xy7dx + cx2y6dy è esatto se
|
(A) c = 7∕2 (B) c = 7 (C) c = 1∕3 (D) c = 1∕7 (E) c = 3 (F) c = 2∕7 |
—————————————————————————
26) Sia f(x,y) = 2x2 + 6xy + cy2. Il suo gradiente è nullo nel punto (4,-8∕3)
|
(A) per qualunque valore di c (B) per nessun valore di c (C) se c = 4∕3 (D) se c = 2∕9 (E) se c = 1∕2 (F) se c = 9∕2 |
—————————————————————————
27) Sia f(x,y) una funzione tale che
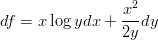
|
(A) log 3 (B) 2 log 2 (C) 2 log 3 (D) 2 (E) 4 (F) log 2 (G) 3 (H) 3 log 2 |
—————————————————————————
28) Il differenziale 3x2 log ydx + 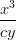 dy è esatto se
dy è esatto se
|
(A) c = 4 (B) c = 1 (C) c = -3 (D) c = -4 (E) c = 3 (F) c = 2 (G) c = -2 (H) c = -1 |
—————————————————————————
|
1 A 2 A 3 E 4 A 5 D 6 C 7 A 8 E 9 B 10 C 11 B 12 A 13 B 14 B 15 A 16 A 17 E 18 B 19 A 20 A 21 A 22 C 23 B 24 E 25 A 26 F 27 F 28 B |
1) Due genitori sono entrambi di genotipo A1A2 (eterozigoti) ad un certo locus. Dunque i figli sono omozigoti A1A1 con probabilità 1∕4, omozigoti A2A2 con probabilità 1∕4, ed eterozigoti A1A2 con probabilità 1∕2. Con quale probabilità, su 4 figli, almeno 2 sono eterozigoti?
|
(A) (B) (C) |
—————————————————————————
2) In quale dei seguenti fenomeni non si può utilizzare la distribuzione binomiale?
(A) il lancio successivo di due monete truccate nello stesso modo
(B) il lancio contemporaneo di due monete non truccate
(C) il lancio successivo di una moneta non truccata e di una moneta truccata
(D) il doppio lancio di una singola moneta non truccata
(E) il doppio lancio di una moneta truccata
—————————————————————————
3) Nel doppio lancio di una moneta truccata, per la quale la probabilità che esca testa è p, il valore p(1 - p) è
(A) la probabilità che escano due teste
(B) la probabilità che esca una testa e una croce
(C) la probabilità che escano due croci
(D) la probabilità che al primo lancio esca testa e al secondo croce
—————————————————————————
4) Nel doppio lancio di una moneta truccata, per la quale la probabilità che esca testa è p, il valore 2p(1 - p) è
(A) la probabilità che escano due croci
(B) la probabilità che al primo lancio esca croce e al secondo testa
(C) la probabilità che al primo lancio esca testa e al secondo croce
(D) la probabilità che esca una testa e una croce
(E) la probabilità che escano due teste
—————————————————————————
5) Nel doppio lancio di una moneta truccata, per la quale la probabilità che esca testa è p, il valore p2 è
(A) la probabilità che escano due teste
(B) la probabilità che esca una testa e una croce
(C) la probabilità che al primo lancio esca testa e al secondo croce
(D) la probabilità che escano due croci
(E) la probabilità che al primo lancio esca croce e al secondo testa
—————————————————————————
6) Per determinare la probabilità che escano due numeri pari come primo estratto sulle ruote di Roma e Milano si può usare la formula per la distribuzione binomiale
|
(A) si (B) no |
—————————————————————————
7) Per determinare la probabilità che escano due numeri pari come primo estratto e secondo estratto sulla ruota di Roma si può usare la formula per la distribuzione binomiale
|
(A) no (B) si |
—————————————————————————
8) In un cassetto ci sono 10 calzini blu e 4 calzini bianchi. Ne vengono presi tre a caso. La probabilità che siano tutti blu può essere calcolata mediante la formula per la distribuzione binomiale
|
(A) no (B) si |
—————————————————————————
9) In un cassetto ci sono 10 calzini blu, 4 calzini bianchi, 10 camice blu e 4 camice bianche. Viene preso a caso un calzino e una camicia. La probailità che siano entrambi blu può essere calcolata mediante la formula per la distribuzione binomiale
|
(A) no (B) si |
—————————————————————————
10) In un cassetto ci sono 10 calzini blu e 4 calzini bianchi. Viene preso un calzino a caso. La probabilità che sia blu è:
|
(A) (B) (C) 10 (D) |
—————————————————————————
11) In una popolazione un gene ha due alleli A e a; dette, rispettivamente, PAA, PAa e Paa le frequenze relative dei genotipi AA, Aa e aa, la frequenza relativa dell’allele A è
|
(A) P AA (B) (C) P AA + PAa (D) P AA + |
—————————————————————————
12) In una popolazione un gene ha due alleli A e a; le frequenze relativa degli omozigoti AA è
|
(A) (B) (C) non si può determinare (D) |
—————————————————————————
13) In una popolazione un gene ha due alleli A e a; la frequenza relativa dell’allele A è p. La frequenza relativa dell’eterozigote, supponendo che sia valida la legge di Hardy-Weimberg, è
|
(A) p(1 - p) (B) (C) 2p(1 - p) (D) p (E) |
—————————————————————————
14) Nel doppio lancio di una moneta truccata, per la quale la probabilità che esca testa è p, il valore 2p(1 - p) è
(A) la probabilità che escano due croci
(B) la probabilità che escano due teste
(C) la probabilità che al primo lancio esca croce e al secondo testa
(D) la probabilità che al primo lancio esca testa e al secondo croce
(E) la probabilità che esca una testa e una croce
—————————————————————————
15) Per determinare la probabilità che escano due numeri pari come primo estratto e secondo estratto sulla ruota di Roma si può usare la formula per la distribuzione binomiale
|
(A) si (B) no |
—————————————————————————
16) In un cassetto ci sono 10 calzini blu, 4 calzini bianchi, 10 camice blu e 4 camice bianche. Viene preso a caso un calzino e una camicia. La probailità che siano entrambi blu può essere calcolata mediante la formula per la distribuzione binomiale
|
(A) no (B) si |
—————————————————————————
17) In una popolazione un gene ha due alleli A e a; dette, rispettivamente, PAA, PAa e Paa le frequenze relative dei genotipi AA, Aa e aa, la frequenza relativa dell’allele A è
|
(A) (B) P AA + (C) P AA (D) P AA + PAa |
—————————————————————————
18) In quale dei seguenti fenomeni non si può utilizzare la distribuzione binomiale?
(A) il lancio successivo di due monete truccate nello stesso modo
(B) il lancio successivo di una moneta non truccata e di una moneta truccata
(C) il doppio lancio di una singola moneta non truccata
(D) il lancio contemporaneo di due monete non truccate
(E) il doppio lancio di una moneta truccata
—————————————————————————
19) Per determinare la probabilità che escano due numeri pari come primo estratto sulle ruote di Roma e Milano si può usare la formula per la distribuzione binomiale
|
(A) si (B) no |
—————————————————————————
20) In una popolazione un gene ha due alleli A e a; le frequenze relativa degli omozigoti AA è
|
(A) (B) (C) non si può determinare (D) |
—————————————————————————
21) Vengono lanciati dei dadi non truccati. Il numero
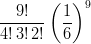
(A) è la probabilità che in 3 lanci di 6 dadi esca 4 volte 1, 3 volte 2, 2 volte 3
(B) è la probabilità che in 9 lanci di un dado esca 4 volte 1, 3 volte 3 e 2 volte 5
(C) è la probabilità che in 3 lanci di un dado esca una volta 4, una volta 3 e una volta 2
—————————————————————————
22) Si consideri un gene biallelico di cui non sono note le caratteristiche selettive; si indichino con P AA , P Aa , Paa le frequenze dei genotipi, e con pA e pa le frequenze degli alleli.
(A) dalle P si possono determinare le p, ma dalle p non si possono determinare le P
(B) dalle p si possono determinare le P, e dalle P si possono determinare le p
(C) dalle p si possono determinare le P, ma dalle P non si possono determinare le p
(D) dalle p non si possono determinare le P, e dalle P non si possono determinare le p
—————————————————————————
23) In un’urna ci sono dieci biglie numerate da 1 a 10. Ne vengono prese a caso due insieme. La probabilità che siano entrambe numerate con un numero dispari si può calcolare con la formula della distribuzione binomiale
|
(A) vero (B) falso |
—————————————————————————
24) In una classe ci sono 10 maschi e 20 femmine. Vengono interrogati insieme due studenti scelti a caso. Detta p la probabilità che siano entrambi maschi.
(A) p non può essere calcolata
(B) p può essere calcolata con la formula della distribuzione binomiale
(C) p non può essere calcolata con la formula della distribuzione binomiale
—————————————————————————
25) In una classe ci sono 10 maschi e 20 femmine. Ogni giorno viene interrogato a caso uno studente, senza escludere quelli già interrogati. La propabilità che il primo studente sia maschio, il secondo femmina e il terzo maschio è
(A) 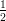 ⋅
⋅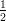 =
= 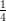
(B) 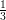 ⋅
⋅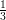 ⋅
⋅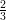 =
= 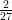
(C) 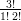
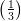 2
2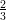 =
= 
—————————————————————————
26) In quale dei seguenti fenomeni non si può utilizzare la distribuzione binomiale?
(A) il doppio lancio di una singola moneta non truccata
(B) il lancio successivo di due monete truccate nello stesso modo
(C) il doppio lancio di una moneta truccata
(D) il lancio contemporaneo di due monete non truccate
(E) il lancio successivo di una moneta non truccata e di una moneta truccata
—————————————————————————
27) Nel doppio lancio di una moneta truccata, per la quale la probabilità che esca testa è p, il valore p(1 - p) è
(A) la probabilità che esca una testa e una croce
(B) la probabilità che al primo lancio esca testa e al secondo croce
(C) la probabilità che escano due teste
(D) la probabilità che escano due croci
—————————————————————————
28) Nel doppio lancio di una moneta truccata, per la quale la probabilità che esca testa è p, il valore 2p(1 - p) è
(A) la probabilità che al primo lancio esca testa e al secondo croce
(B) la probabilità che escano due teste
(C) la probabilità che esca una testa e una croce
(D) la probabilità che al primo lancio esca croce e al secondo testa
(E) la probabilità che escano due croci
—————————————————————————
29) Nel doppio lancio di una moneta truccata, per la quale la probabilità che esca testa è p, il valore p2 è
(A) la probabilità che escano due croci
(B) la probabilità che esca una testa e una croce
(C) la probabilità che escano due teste
(D) la probabilità che al primo lancio esca testa e al secondo croce
(E) la probabilità che al primo lancio esca croce e al secondo testa
—————————————————————————
30) Per determinare la probabilità che escano due numeri pari come primo estratto sulle ruote di Roma e Milano si può usare la formula per la distribuzione binomiale
|
(A) si (B) no |
—————————————————————————
31) Per determinare la probabilità che escano due numeri pari come primo estratto e secondo estratto sulla ruota di Roma si può usare la formula per la distribuzione binomiale
|
(A) si (B) no |
—————————————————————————
32) In un cassetto ci sono 10 calzini blu e 4 calzini bianchi. Ne vengono presi tre a caso. La probabilità che siano tutti blu può essere calcolata mediante la formula per la distribuzione binomiale
|
(A) no (B) si |
—————————————————————————
33) In un cassetto ci sono 10 calzini blu, 4 calzini bianchi, 10 camice blu e 4 camice bianche. Viene preso a caso un calzino e una camicia. La probailità che siano entrambi blu può essere calcolata mediante la formula per la distribuzione binomiale
|
(A) si (B) no |
—————————————————————————
34) In un cassetto ci sono 10 calzini blu e 4 calzini bianchi. Viene preso un calzino a caso. La probabilità che sia blu è:
|
(A) (B) (C) 10 (D) |
—————————————————————————
35) In una popolazione un gene ha due alleli A e a; dette, rispettivamente, PAA, PAa e Paa le frequenze relative dei genotipi AA, Aa e aa, la frequenza relativa dell’allele A è
|
(A) (B) P AA + PAa (C) P AA (D) P AA + |
—————————————————————————
36) In una popolazione un gene ha due alleli A e a; le frequenze relativa degli omozigoti AA è
|
(A) non si può determinare (B) (C) (D) |
—————————————————————————
37) In una popolazione un gene ha due alleli A e a; la frequenza relativa dell’allele A è p. La frequenza relativa dell’eterozigote, supponendo che sia valida la legge di Hardy-Weinberg, è
|
(A) p (B) 2p(1 - p) (C) (D) p(1 - p) (E) |
—————————————————————————
38) Un indicatore di quanto sono dispersi dei dati x1, …xn è
|
(A) la varianza (B) la mediana (C) la media |
—————————————————————————
39) Due distribuzioni normali, con la stessa media e la stessa varianza
|
(A) possono essere diverse (B) sono uguali |
—————————————————————————
40) La distribuzione esponenziale è utile per descrivere gli errori che si ottengono sommando molte variabili casuali
|
(A) vero (B) falso |
—————————————————————————
41) In quale dei seguenti fenomeni non si può utilizzare la distribuzione binomiale?
(A) il doppio lancio di una moneta truccata
(B) il lancio successivo di due monete truccate nello stesso modo
(C) il lancio contemporaneo di due monete non truccate
(D) il lancio successivo di una moneta non truccata e di una moneta truccata
(E) il doppio lancio di una singola moneta non truccata
—————————————————————————
42) Per determinare la probabilità che escano due numeri pari come primo estratto sulle ruote di Roma e Milano si può usare la formula per la distribuzione binomiale
|
(A) si (B) no |
—————————————————————————
43) In una popolazione un gene ha due alleli A e a; le frequenze relativa degli omozigoti AA è
|
(A) (B) non si può determinare (C) (D) |
—————————————————————————
44) Per una gene biallelico in una popolazione, dalle frequenze dei genotipi si posso sempre determinare le frequenze alleliche
|
(A) falso (B) vero |
—————————————————————————
45) Per una moneta truccata la probabilità che esca testa sia 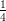 . In media, quante teste escono su due
lanci? (cioè ripetendo più volte il doppio lancio della moneta, quante teste escono in media in un
doppio lancio ?)
. In media, quante teste escono su due
lanci? (cioè ripetendo più volte il doppio lancio della moneta, quante teste escono in media in un
doppio lancio ?)
|
(A) (B) (C) (D) (E) (F) |
—————————————————————————
46) Un gene si presenta nelle due varianti A e a. In una famiglia di due figli, i genitori sono entrambi eterozigoti. Con che probabilità i due genotipi dei figli sono AA e AA?
|
(A) (B) (C) (D) |
—————————————————————————
47) In quale dei seguenti fenomeni non si può utilizzare la distribuzione binomiale?
(A) il doppio lancio di una singola moneta non truccata
(B) il doppio lancio di una moneta truccata
(C) il lancio successivo di due monete truccate nello stesso modo
(D) il lancio successivo di una moneta non truccata e di una moneta truccata
(E) il lancio contemporaneo di due monete non truccate
—————————————————————————
48) In una popolazione un gene ha due alleli A e a; le frequenze relativa degli omozigoti AA è
|
(A) (B) (C) i dati non sono sufficienti (D) |
—————————————————————————
49) In una classe ci sono 10 maschi e 20 femmine. Vengono interrogati insieme due studenti scelti a caso. Detta p la probabilità che siano entrambi maschi.
(A) p non può essere calcolata con la formula della distribuzione binomiale
(B) p non può essere calcolata
(C) p può essere calcolata con la formula della distribuzione binomiale
—————————————————————————
50) In una classe ci sono 10 maschi e 20 femmine. Ogni giorno viene interrogato a caso uno studente, senza escludere quelli già interrogati. La propabilità che il primo studente sia maschio, il secondo femmina e il terzo maschio è
(A) 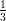 ⋅
⋅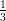 ⋅
⋅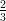 =
= 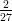
(B) 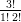
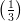 2
2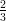 =
= 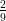
(C) 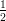 ⋅
⋅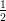 =
= 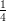
—————————————————————————
51) Sia x1 = 5, x2 = 2, x3 = -2.
|
(A) la mediana è (B) la mediana è -2 (C) la mediana è 5 (D) la mediana è 2 |
—————————————————————————
52) Per indentificare una particolare distribuzione uniforme è sufficiente assegnare il valore della media
|
(A) vero (B) falso |
—————————————————————————
53) Si considerino i dati (1, - 5, - 3, 0). La mediana è -4
|
(A) falso (B) vero |
—————————————————————————
54) In un’urna ci sono 10 palline rosse e 8 bianche. Ne vengono estratte due insieme. Per determinare la probabilità che solo una di esse sia rossa si può utilizzare la formula binomiale?
|
(A) no (B) si |
—————————————————————————
55) Vengono lanciate in sequenza due monete non truccate. Gli eventi TC e CT sono
|
(A) incompatibili (B) indipendenti |
—————————————————————————
56) Si consideri la seguente tabella di dati e frequenze
| -2 | 40 |
| 0 | 20 |
| 8 | 20 |
La varianza è
|
(A) 18 (B) 15/2 (C) 17 (D) 14 (E) 8 |
—————————————————————————
57) Una moneta non truccata viene lanciata 4 volte. La probabilità che escano due teste e due croci è
(A) 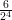
(B) 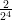
(C) 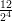
(D) 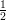
(E) 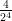
—————————————————————————
58) In un gioco, si lancia una moneta non truccata. Se esce T, si vince; altrimenti si lancia un dado non truccato. Se esce 5 o 6 si vince. La probabilità di vincere è
|
(A) 3/5 (B) 2/3 (C) 5/6 (D) 1/6 (E) 1/3 |
—————————————————————————
59) In un lungo viaggio in moto, la probabilità che si fori la ruota anteriore è 2∕5, che si fori quella posteriore è 2∕7. Con che probabilità si fora una ruota?
|
(A) 4∕7 (B) 24∕35 |
—————————————————————————
60) Vengono lanciate insieme due monete truccate. Per la prima la probabilità di T è  , per la seconda
è
, per la seconda
è  . La probabilità che escano una T e una C è
. La probabilità che escano una T e una C è
|
(A) 4∕9 (B) 1∕12 (C) 1∕4 (D) 1∕6 (E) 1∕2 (F) 5∕12 |
—————————————————————————
61) Tre monete vengono lanciate consecutivamente. Lo spazio degli eventi è
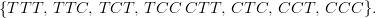
(A) {T T T, TTC, CTT, CTC}
(B) {T T T, TCT, CTT, CCT}
(C) {T CT, TCC, CCT, CCC}
(D) {CT T, CTC, CCT, CCC}
(E) {T T C, TCC, CTC, CCC}
(F) {T T T, TTC, TCT, TCC}
(G) nessuno degli altri
—————————————————————————
62) Un gene di alleli “A” e “a” è indipendente da un altro gene di alleli “B” e “b”. Supponendo che una coppia di genitori sia di genotipi AaBb e AaBb, con quale probabilità, su 4 figli, esattamente 1 figli saranno di genotipo AABB?
(A) 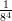 ⋅ 6 ⋅ 72 = 147∕2048 = 0.0717773...
⋅ 6 ⋅ 72 = 147∕2048 = 0.0717773...
(B) 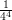 ⋅ 4 ⋅ 3 = 3∕64 = 0.046875
⋅ 4 ⋅ 3 = 3∕64 = 0.046875
(C) 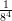 ⋅ 4 ⋅ 73 = 343∕1024 = 0.3349609...
⋅ 4 ⋅ 73 = 343∕1024 = 0.3349609...
(D) 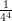 ⋅ 6 ⋅ 32 = 27∕128 = 0.2109375
⋅ 6 ⋅ 32 = 27∕128 = 0.2109375
(E) 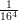 ⋅ 4 ⋅ 153 = 3375∕16384 = 0.2059937...
⋅ 4 ⋅ 153 = 3375∕16384 = 0.2059937...
(F) 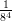 ⋅ 4 ⋅ 7 = 7∕1024 = 0.0068359...
⋅ 4 ⋅ 7 = 7∕1024 = 0.0068359...
(G) 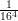 ⋅ 4 ⋅ 15 = 15∕16384 = 0.0009155...
⋅ 4 ⋅ 15 = 15∕16384 = 0.0009155...
(H) 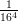 ⋅ 6 ⋅ 152 = 675∕32768 = 0.0205994...
⋅ 6 ⋅ 152 = 675∕32768 = 0.0205994...
(I) 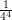 ⋅ 4 ⋅ 33 = 27∕64 = 0.421875
⋅ 4 ⋅ 33 = 27∕64 = 0.421875
—————————————————————————
63) Per il lancio di una moneta la probabiità che esca T è 1/4. Gli eventi “esce T” e “esce C” sono
|
(A) indipendenti (B) incompatibili (C) equiprobabili |
—————————————————————————
64) In una classe di 30 maschi e 50 femmine, l’altezza media dei maschi è 1.78, l’altezza media delle femmine è 1.70. L’altezza media di un individuo della classe è
|
(A) 1.75 (B) 1.74 (C) 1.72 (D) 1.73 |
—————————————————————————
65) La probabilità di contrarre il raffreddore per un contatto con un soggetto infetto è di un centesimo. Supponendo che un individuo abbia 50 contatti con soggetti infetti, determinare la probabilità che egli ha di contrarre il raffreddore.
(A) 1 - 0.0150 ≃ 1
(B) 1 - (1 - 0.01)50 ≃ 0.39
(C) 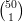 0.011 ⋅ 0.9949 ≃ 0.306
0.011 ⋅ 0.9949 ≃ 0.306
(D) 50 ⋅ 0.01 = 1∕2
(E) 1 - 50 ⋅ 0.01 = 1∕2
(F) (1 - 0.01)50 ≃ 0.61
(G) 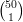 0.0149 ⋅ 0.991 ≃ 0
0.0149 ⋅ 0.991 ≃ 0
—————————————————————————
66) Per una moneta la probabilità che esca T è 1/3, per un’altra è 1/4. Vengono lanciate insieme. Per determinare la probabilità che esca una sola T si può usare la distribuzione binomiale.
|
(A) falso (B) vero |
—————————————————————————
67) Per una moneta la probabilità che esca T è 1/3, per un’altra è 3/4. Vengono lanciate insieme. La probabilità che esca una sola T è:
|
(A) 4/9 (B) 3/4 (C) 3/8 (D) 1/3 (E) 7/12 |
—————————————————————————
68) Un dado non truccato viene lanciato tre volte. La probabilità che escano due sei e un cinque è
(A) 1∕6 ⋅ 1∕6 ⋅ 1∕6 = 1∕216
(B) 6∕6 ⋅ 6∕6 ⋅ 5∕6 = 5∕6
(C) 3∕216 = 1∕72
—————————————————————————
69) Un dado non truccato viene lanciato tre volte. Determinare la probabilità che la somma dei punteggi usciti sia 4
(A) 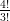 ⋅ 4∕216 = 1∕54
⋅ 4∕216 = 1∕54
(B) 3∕216 = 1∕72
(C) 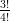 ⋅ 1∕216 = 1∕864
⋅ 1∕216 = 1∕864
—————————————————————————
70) Un dado non truccato viene lanciato due volte. Determinare la probabilità che la somma dei punteggi sia 11.
(A) 2 ⋅ 11∕36 = 11∕18
(B) 1/36
(C) 2∕36 = 1∕18
(D) 11/36
(E) 3∕36 = 1∕12 —————————————————————————
71) Un gene ha alleli A e a. La frequenza dell’allele A nella popolazione è 1/10. Determinare la frequenza dell’eterozigote Aa supponendo valida la legge di HW.
|
(A) 9∕50 (B) 9∕10 + 1∕10 = 1 (C) 1∕100 (D) 9∕10 (E) 9∕100 (F) 1∕10 |
—————————————————————————
72) Per un gene biallelico, le frequenze dei genotipi nella popolazione sono AA: 40%, Aa: 10%, aa: 50%. Determinare la frequenza dell’allele A nella popolazione
|
(A) 55% (B) 40% (C) 45% |
—————————————————————————
73) Per un gene biallelico, le frequenze dei genotipi nella popolazione sono AA: 40%, Aa: 10%, aa: 50%. Per questo gene vale la legge di HW?
|
(A) no (B) si (C) non si può decidere |
—————————————————————————
74) Un apparato meccanico ha due elementi soggetti a rottura irreparabile. In 5 anni, la probabilità che si rompa il primo è 2∕5, che si rompa il secondo è 2∕7. Con che probabilità in 5 anni l’apparato si rompe?
|
(A) 4∕7 (B) 24∕35 |
—————————————————————————
75) Si considerino i dati 14, 12, 15. La media è minore della mediana?
|
(A) no (B) si |
—————————————————————————
76) In un gioco con due monete, si vince se escono due T o due C. Le monete sono truccate: per la
prima la probabilità di T è  , per la seconda è
, per la seconda è  .
.
La probabilità di perdere è
|
(A) 4∕9 (B) 1∕2 (C) 5∕12 (D) 1∕4 (E) 1∕12 (F) 1∕6 |
—————————————————————————
77) In una popolazione un gene si presenta in due varianti, A e a. Le frequenze relative dei genotipi nella popolazione sono P(AA) = 0.0121, P(aa) = 0.7921, P(Aa) = 0.1958. È valida la legge di Hardy-Weinberg?
|
(A) non si può rispondere (B) si (C) no |
—————————————————————————
78) Un gene si presenta in tre varianti A1, A2, A3. In una popolazione le frequenze relative dei tre alleli sono, rispettivamente, 0.11, 0.76, 0.13. Nelle ipotesi di accoppiamenti casuali, di popolazione infinita, di irrilevanza del gene per la selezione, quale sarà la frequenza relativa del genotipo A1A3 nella generazione successiva?
|
(A) 0.01925 (B) 0.0143 (C) 0.00715 (D) 0.0286 (E) 0.24 (F) 0.02405 |
—————————————————————————
79) Un gene si presenta nelle due varianti A e a. Una coppia di genitori eterozigoti ha 7 figli. Quantè la probabilità che 1 siano di genotipo Aa, 1 di genotipo AA e 5 di genotipo aa? (Attenzione, le potenze di due non sono state semplificate)
|
(A) (B) (C) (D) (E) (F) |
—————————————————————————
80) Si consideri il seguente gioco con una moneta truccata per la quale P(C) = 1∕3. Se esce croce si perdono 3 euro, se esce testa la moneta viene lanciata di nuovo; se al secondo lancio esce testa si vincono 3 euro, altrimenti si vincon 2 euro. Quant’è la vincita media per una mano di gioco?
|
(A) (B) (C) (D) |
—————————————————————————
81) Una popolazione di insetti viene trattata con un insetticida che è particolarmente efficace su un dato genotipo. Dopo il trattamento, per un gene di alleli A e a si misurano le frequenze dei genotipi, che risultato essere pAA = 0.1, pAa = 0.3, paa = 0.6. In assenza di altri trattamenti selettivi, supponendo la casualità degli accoppiamenti e molto numerosa la popolazione, qual è il valore della frequenza del genotipo AA nelle generazioni succesive?
|
(A) 0.1 (B) 0.01 (C) 0.25 (D) 0.0625 |
—————————————————————————
82) In una popolazione, per un carattere si osservano i fenotipi F e f, per un altro carattere i fenotipi G e g. La frequenza relativa degli individui di fenotipo F sul totale della popolazione è 0.4, quella degli individui di fenotipo G è 0.1. Nell’ipotesi che i geni che determinano i due caratteri si trasmettano in modo indipendente, quant’è la frequenza relativa degli individui di fenotipo F g?
|
(A) 0.54 (B) 0.06 (C) 0.04 (D) 0.36 |
—————————————————————————
83) In una popolazione, per un carattere si osservano i fenotipi F e f, per un altro carattere i fenotipi G e g. Vengono misurate le frequenze dei fenotipi accoppiati FG, Fg, fG, fg, ottenendo la seguente tabella:
| F | f | |
| G | 0.03 | 0.27 |
| g | 0.07 | 0.63 |
Qual è la frequenza degli individui di fenotipo f sul totale della popolazione?
|
(A) 0.0021 (B) 0.1 (C) 0.0081 (D) 0.9 (E) 0.1701 (F) 0.3 (G) 0.0441 (H) 0.7 |
—————————————————————————
84) In una popolazione un gene si presenta in due varianti, A e a, con A dominante. Le distribuzioni degli alleli e dei genotipi verificano l’equilibrio di Hardy-Weinberg. La frequenza di A nella popolazione è 0.05. Quant’è nella popolazione la frequenza del fenotipo dominante?
|
(A) 0.9975 (B) 0.0975 (C) 0.05 (D) 0.0025 |
—————————————————————————
85) In una popolazione un gene si presenta nelle varianti, A e a, e un altro nelle varianti B e b. Le distribuzioni alleliche dei geni e dei relativi genotipi verificano l’equilibrio di Hardy-Weinberg. La frequenza di A nella popolazione è 0.1, la frequenza di B è 0.2. Supponendo indipendenti le distribuzioni dei due geni, quant’è nella popolazione la frequenza degli individui di genotipo AaBb?
|
(A) 0.0288 (B) 0.0576 (C) 0.0392 (D) 0.0144 |
—————————————————————————
86) In una popolazione un gene si presenta nelle varianti, A e a, con A dominante, e un altro nelle varianti B e b, con B dominate. Le distribuzioni alleliche dei geni e dei relativi genotipi verificano l’equilibrio di Hardy-Weinberg. La frequenza di A nella popolazione è 0.1, la frequenza di B è 0.2. Supponendo indipendenti le distribuzioni dei due geni, quant’è nella popolazione la frequenza degli individui di fenotipo AB, cioè dominante contemporaneamente per i due geni?
|
(A) 0.1368 (B) 0.0342 (C) 0.2432 (D) 0.5184 (E) 0.5832 (F) 0.0608 (G) 1.0368 (H) 0.0684 (I) 0.2592 (J) 0.1458 (K) 0.2916 (L) 0.1216 |
—————————————————————————
87) Quante sono le possibili sequenze di 11 basi di DNA che contengono sei A, tre C, una G e una T?
|
(A) 4620 (B) 6160 (C) 18480 (D) 9240 |
—————————————————————————
88) Quante sono le possibili sequenze di DNA lunghe 4 che non contengono basi ugali?
|
(A) 47 (B) 32 (C) 31 (D) 11 (E) 12 (F) 48 (G) 63 (H) 4 (I) 64 (J) 3 (K) 23 (L) 24 |
—————————————————————————
|
1 A 2 C 3 D 4 D 5 A 6 A 7 A 8 A 9 B 10 B 11 D 12 C 13 C 14 E 15 B 16 B 17 B 18 B 19 A 20 C 21 B 22 A 23 B 24 C 25 B 26 E 27 B 28 C 29 C 30 A 31 B 32 A 33 A 34 D 35 D 36 A 37 B 38 A 39 B 40 B 41 D 42 A 43 B 44 B 45 A 46 A 47 D 48 C 49 A 50 A 51 D 52 B 53 A 54 A 55 A 56 C 57 A 58 B 59 A 60 F 61 F 62 E 63 B 64 D 65 B 66 A 67 E 68 C 69 B 70 C 71 A 72 C 73 A 74 A 75 B 76 C 77 B 78 D 79 A 80 D 81 D 82 D 83 D 84 B 85 B 86 H 87 D 88 L |
1) Avete piantato 10000 semi, per ognuno dei quali la probabilità di germinare è dell’80% ma nascono solo 7000 piante. Sospettate che vi abbiano truffato mescolando ai semi da voi richiesti anche quelli di una varietà meno costosa, per i quali la probabilità di germinare è solo del 40%. Date un valore alla percentuale di semi scadenti sul totale che vi è stato venduto.
|
(A) 3/4 (B) 1/4 (C) 1/2 (D) 3/5 (E) 1/5 (F) 2/5 |
—————————————————————————
2) Per la varietà A di una pianta i semi germinano nel 60% dei casi, per la varietà B nell’80%. Su 10000 semi ne germinano 7000. Quant’è la frazione di piante della varietà A che si ottiene?
|
(A) 1/2 (B) 3/7 (C) 5/7 (D) 3/4 (E) 3/5 (F) 4/5 |
—————————————————————————
3) Un test diagnostico ha sensibilità del 90%, e specificità del 70%. Un controllo di massa vi dà nella metà dei casi esito positivo. Quant’è la probabilità che un individuo sia malato se il test dà risultato positivo?
|
(A) 0.9 (B) 0.3 (C) 0.4 (D) 0.2 (E) 0.8 (F) 0.6 (G) 0.5 (H) 0.1 (I) 0.7 |
—————————————————————————
4) Un test diagnostico ha sensibilità del 90%, e specificità del 70%. Un controllo di massa dà nella metà dei casi esito positivo. Quant’è la frazione di individui che sono malati e risultano positivi al test, sul totale della popolazione?
|
(A) 0.6 (B) 0.3 (C) 0.9 (D) 0.2 (E) 0.4 (F) 0.5 (G) 0.1 (H) 0.8 (I) 0.7 |
—————————————————————————
5) L’esprimersi di un gene G influenza la possibilità di contrarre una malattia M. Il 70% degli individui malati e il 10% degli indivuidi sani hanno il G espresso. Si supponga che, in una popolazione, 3 individui su 1000 siano malati; se un individuo ha G espresso, con che probabilità, approssimativamente, è malato?
|
(A) 23.333 su cento (B) 0.670 su cento (C) 60.000 su cento (D) 20.000 su cento (E) 2.063 su cento (F) 70.000 su cento (G) 1.444 su cento (H) 69.820 su cento (I) 0.895 su cento |
—————————————————————————
6) Un filtro controlla la vostra posta elettronica, mettendo da parte la posta indesiderata (pubblicità, richieste di denaro, truffe, virus ...). Su 100 mail indesiderate, il filtro ne mette da parte 90, le altre le lascia passare; su 100 mail buone, il filtro ne mette da parte 20 e le altre le lascia passare. Su 1000 mail che vi sono arrivate, il fitro ne ha messe da parte 340. Approssimativamente, quante mail effettivamente indesiderate vi sono state inviate?
(A) 800
(B) 818
(C) 490
(D) 900
(E) 372
(F) 834
(G) 438
(H) 398
(I) 850
(J) 200
(K) 278
—————————————————————————
7) I semi di una pianta a fiore rosso germinano nell’60% dei casi, quelli della variante a fiore bianco nel 90% dei casi. In una scatola ci sono 40 semi “a fiore rosso”, e 80 “a fiore bianco”. Prendendo un seme a caso, la probabilità che germini è:
(A) 0.65
(B) 0.85
(C) 0.7
(D) 0.9
(E) 0.8
(F) 0.6
(G) 0.75
—————————————————————————
8) La sensibilità di un test diagnostico è del 60%, la specificità è dell’80%. Un individuo viene sottoposto al test e risulta negativo. La probabilità che l’individuo sia sano è
(A) 0.8
(B) 0.9
(C) 0.7
(D) non si può determinare
(E) 0.6
—————————————————————————
9) La sensibilità di un test diagnostico è del 52%, la specificità è del 98%. Su 100000 individui risultano 10000 test positivi. Una stima del numero di malati è
|
(A) 5200 (B) 9800 (C) 200 (D) 10000 (E) 4800 (F) 16000 |
—————————————————————————
10) Un filtro controlla la vostra posta elettronica, mettendo da parte la posta indesiderata (pubblicità, richieste di denaro, truffe, virus ...). Il filtro intercetta e mette da parte Il 70% delle mail indesiderate e il 10% delle mail buone. Si supponga che su 1000 mail, 3 siano indesiderate. Tra le mail intercettate, quant’è, approssimativamente, la frequenza relativa delle mail effettivamente indesiderate?
|
(A) 60.000 su cento (B) 1.444 su cento (C) 0.895 su cento (D) 70.000 su cento (E) 0.670 su cento (F) 23.333 su cento (G) 20.000 su cento (H) 2.063 su cento (I) 69.820 su cento |
—————————————————————————
11) L’esprimersi di un gene G influenza la possibilità di contrarre una malattia. Su 100 individui malati, 90 hanno G espresso; su 100 sani, 20 hanno G espresso. Viene fatto un controllo per il gene su 1000 persone. Di esse, 340 risultano avere G espresso, quante sono, approssimativamente, le persone effettivamente malate?
(A) 818
(B) 850
(C) 490
(D) 278
(E) 900
(F) 398
(G) 834
(H) 200
(I) 372
(J) 438
(K) 800
—————————————————————————
12) Una piantaggione di mais tradizionale e transgenico viene trattata con un erbicida. L’erbicida uccide il 80% delle piante di mais tradizionali, e il 30% della piante della varietà transgenica. Quanto deve essere la frazione di piante transgeniche sul totale per assicurarsi che dopo il trattamento con l’erbicida sopravviva almeno il 55% delle piante?
|
(A) (B) (C) (D) (E) (F) |
—————————————————————————
13) Un test diagnostico dà risultato positivo per 80 individui malati su 100, e per 10 individui sani su 100. Ad un controllo di massa, risulta positivo al test il 75% della popolazione. Quant’è la frazione di popolazione malata sul totale?
|
(A) 1∕14 (B) 11∕14 (C) 1∕8 (D) 13∕14 (E) 3∕14 (F) 2∕15 |
—————————————————————————
14) Un erbicida uccide il 30% delle piante di una varietà transgenica di mais, e il 80% della varietà selvaggia. Viene trattata una piantaggione mista, che contiene il 40% di piante della varietà selvaggia. Determinare la frazione delle piante della varietà selvaggia sul totale delle piante uccise.
|
(A) 16∕25 (B) 8∕11 (C) 1∕2 (D) 3∕5 |
—————————————————————————
15) In una popolazione un gene si presenta in due varianti, A e a, con A dominante. L’essere di fenotipo A o a incide sulla probabilità di contrarre una malattia, ormai diffusa endemicamente nella popolazione. La probabilità che un individuo di fenotipo A abbia contratto la malattia è 0.1, di un individuo di fenotipo a è 0.2. La malattia colpisce 16 individui su 100. Quant’è la frequenza di individui di fenotipo A nella popolazione?
|
(A) 4/5 (B) 3/5 (C) 1/5 (D) 3/4 (E) 1/4 (F) 2/5 |
—————————————————————————
16) In una popolazione un gene si presenta in due varianti, A e a, con A dominante. L’essere di fenotipo A o a incide sulla probabilità di contrarre una malattia, ormai diffusa endemicamente nella popolazione. La probabilità che un individuo di fenotipo A abbia contratto la malattia è 0.1, di un individuo di fenotipo a è 0.2. È noto che due quinti della popolazione è di fenotipo A. Determinare la frequenza di individui di fenotipo A tra gli individui malati (cioè il numero di individui di fenotipo A e malati, diviso il numero di malati, o anche, in termini probabilistici, la probabilità di essere di fenotipo A se si è malati).
|
(A) 3 / 5 (B) 1 / 7 (C) 3 / 7 (D) 2 / 3 (E) 1 / 4 (F) 1 / 9 |
—————————————————————————
17) In referendum, alcuni partiti si sono schierati per il ’no’ (partiti C=contrari), una parte per il ’si’ (partiti F=favorevoli). Tra gli elettori dei partiti C, 10 su 100 hanno votato ’no’, tra gli elettori dei partiti F, 20 su 100 hanno votato ’no’. Il ’no’ viene votato complessivamente da 16 cittadini su 100. In base a questi dati, quale frazione degli elettori vota per i partiti C?
|
(A) 1/5 (B) 3/4 (C) 1/4 (D) 3/5 (E) 2/5 (F) 4/5 |
—————————————————————————
18) In referendum, alcuni partiti si sono schierati per il ’no’ (partiti C=contrari), una parte per il si (partiti F=favorevoli). Tra gli elettori dei partiti C, 10 su 100 hanno votato ’no’, tra gli elettori dei partiti F, 20 su 100 hanno votato ’no’. Supponendo che gli elettori dei partiti C siano due quinti della popolazione, quale frazione dei cittadini che hanno votato ’no’ sono elettori dei partiti C?
|
(A) 3 / 5 (B) 1 / 4 (C) 1 / 9 (D) 2 / 3 (E) 3 / 7 (F) 1 / 7 |
—————————————————————————
|
1 B 2 B 3 F 4 B 5 E 6 J 7 E 8 D 9 F 10 H 11 H 12 F 13 D 14 A 15 F 16 E 17 E 18 B |
1) Un numero reale x  [0, 5] viene estratto con una densità di probabilità g(x) che vale
[0, 5] viene estratto con una densità di probabilità g(x) che vale 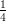 per x
per x  [0, 2]
e vale una costante c per x
[0, 2]
e vale una costante c per x  [2, 5]. Il valore di c deve essere:
[2, 5]. Il valore di c deve essere:
(A) nessuna delle altre
(B) 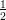
(C) 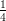
(D) 
(E) 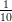
(F) 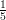
(G) 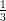
—————————————————————————
2) Un numero reale x  [0, 5] viene estratto con una densità di probabilità g(x) che vale
[0, 5] viene estratto con una densità di probabilità g(x) che vale 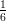 per x
per x  [0, 2]
e
[0, 2]
e  per x
per x  [2, 5]. Il valor medio di x è:
[2, 5]. Il valor medio di x è:
|
(A) (B) (C) (D) 12 (E) 2 (F) (G) 1 (H) nessuna delle altre |
—————————————————————————
3) Un numero reale x  [0, 2] viene estratto con una densità di probabilità g(x) =
[0, 2] viene estratto con una densità di probabilità g(x) = 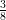 x2. La probabilità
che x <
x2. La probabilità
che x < 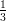 è:
è:
(A) 0
(B) 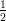
(C) 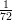
(D) 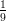
(E) 1
(F) 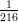
(G) 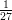
—————————————————————————
4) Un numero reale x  [0, 5] viene estratto con una densità di probabilità g(x) che vale a per
0 ≤ x < 2 e b per 2 ≤ x ≤ 5. Sapendo che la probabilità di trovare x tra 2 e 5 è due volte la probabilità
di trovarlo tra 0 e 2, qual è il valore di a?
[0, 5] viene estratto con una densità di probabilità g(x) che vale a per
0 ≤ x < 2 e b per 2 ≤ x ≤ 5. Sapendo che la probabilità di trovare x tra 2 e 5 è due volte la probabilità
di trovarlo tra 0 e 2, qual è il valore di a?
|
(A) (B) (C) (D) (E) (F) |
—————————————————————————
5) Un numero x  [-5, 5] viene estratto con una densità di probabilità g(x) che vale
[-5, 5] viene estratto con una densità di probabilità g(x) che vale 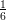 per x
per x  [-2, 2],
[-2, 2],
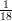 per x
per x  [2, 5] e ancora
[2, 5] e ancora 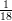 per x
per x  [-5,-2]. Il valore aspettato di x è
[-5,-2]. Il valore aspettato di x è
|
(A) -2 (B) 3 (C) 0 (D) 2 (E) -5 |
—————————————————————————
6) Un numero reale x  [-2, 2] viene estratto con densità di probabilità g(x), che vale a in [-2, 0) e b
in [0, 2]. Il valor medio di x è
[-2, 2] viene estratto con densità di probabilità g(x), che vale a in [-2, 0) e b
in [0, 2]. Il valor medio di x è 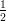 . Il valore di b è
. Il valore di b è
(A) 1
(B) 
(C) 0
(D) 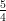
(E) 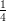
(F) 
(G) 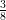
—————————————————————————
7) Un numero x viene estratto con una legge di probabilità uniforme. È noto che il minimo valore che x
può assumere è 2, e che la probabilità che 2 ≤ x ≤ 8 è 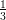 . Quant’è il massimo che x può
assumere?
. Quant’è il massimo che x può
assumere?
|
(A) (B) 20 (C) 4 |
—————————————————————————
8) Un numero x è estratto uniformemente nell’intervallo [2, 4]. Per ogni z  [2, 4], la probabilità P(z)
che z ≤ x ≤ 4 è
[2, 4], la probabilità P(z)
che z ≤ x ≤ 4 è
|
(A) (B) (C) (D) (E) (F) |
—————————————————————————
9) La variabile aleatoria continua x assume valori nell’intervallo [0, 2].
È noto che P(x  [0,z]) =
[0,z]) = 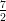 z -
z -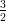 z2. La densità di probabilità è
z2. La densità di probabilità è
(A) ρ(x) = 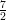 - 3x
- 3x
(B) ρ(x) = 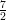 x -
x - x2
x2
(C) ρ(x) = 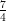 x2 -
x2 -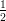 x3
x3
—————————————————————————
10) Una variabile aleatoria viene estratta con distribuzione esponenziale di media 2. Quant’è la probabilità che essa sia compresa nell’intervallo [6, 10] ?
(A)  ∕2
∕2
(B) e-3 - e-5
(C) 2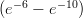
(D) 2
(E) 2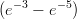
(F) e-12 - e-20
(G)  ∕2
∕2
(H) e-6 - e-10
(I) 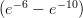 ∕2
∕2
—————————————————————————
11) Una variabile aleatoria reale assume valori nell’intervallo [-1, 1], con densità di probabilità ρ(x) = 1 -|x|. Il valor medio di x22 è
|
(A) 1 (B) 1∕276 (C) 1∕22 (D) 1∕552 (E) 1∕11 (F) 1∕253 |
—————————————————————————
12) Un numero x viene estratto con densità di probabilità uniforme nell’intervallo [3, 9]. La probabilità che esso sia compreso nell’intervallo [5, 8] è
|
(A) (B) (C) |
—————————————————————————
13) Un numero reale x viene estratto nell’intervallo [0, 24] con la densità di probabilità
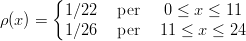
|
(A) 12 (B) 23∕2 (C) 59∕4 (D) 11 (E) 83∕4 (F) 85∕4 (G) 25∕2 (H) 61∕4 |
—————————————————————————
14) Un numero reale x viene estratto nell’intervallo [0, 24] con la densità di probabilità
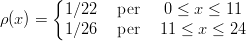
|
(A) 1∕11 (B) 1∕13 (C) 1∕24 (D) 1∕2 (E) 1∕22 (F) 1∕26 |
—————————————————————————
15) Un numero reale x è estratto nell’intervallo [0, 1∕3] con densità di probabilità data da
ρ(x) = 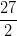 (2x - 3x2). Il valore medio di x è
(2x - 3x2). Il valore medio di x è
|
(A) 1∕3 (B) 1∕6 (C) 5∕24 (D) 1∕2 (E) 1 (F) 7∕8 |
—————————————————————————
16) Un numero reale viene estratto nell’intervallo [0, 2∕3] con una certa legge. La probabilità
che esso sia nell’intervallo [0,x] è 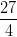 (x2 - x3). La densità di probabilità nel punto 1∕3
è
(x2 - x3). La densità di probabilità nel punto 1∕3
è
|
(A) 5∕12 (B) 9∕4 (C) 0 (D) 3∕2 (E) 9∕2 |
—————————————————————————
17) Un numero reale x viene estratto nell’intervallo [0, 24] con la densità di probabilità
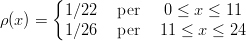
|
(A) 37∕286 (B) 12∕143 (C) 24∕143 (D) 35∕286 (E) 6∕143 |
—————————————————————————
18) Un numero reale x  [0, 3] viene estratto con densità di probabilità
[0, 3] viene estratto con densità di probabilità  (3 - x). Il suo valore medio
è
(3 - x). Il suo valore medio
è
|
(A) 0 (B) 1 (C) 9∕4 (D) 2 (E) 3∕2 (F) 3∕4 |
—————————————————————————
|
1 D 2 A 3 F 4 E 5 C 6 G 7 B 8 B 9 A 10 B 11 B 12 C 13 B 14 D 15 C 16 B 17 D 18 B |